【北师大版·数学】2024年中考一轮复习之整式

试卷更新日期：2023-12-05 类型：一轮复习

进入出卷网下载

一、选择题

1. 下列运算正确的是（）

A、x⁵+x⁵=x¹⁰ B、（x³y²）²=x⁵y⁴ C、x⁶÷x²=x³ D、x²·x³=x⁵

查看试题解析
2. 电子文件的大小常用 $B, K B, M B, G B$ 等作为单位，其中 $1 G B = 2^{10} M B, 1 M B = 2^{10} K B, 1 K B = 2^{10} B$ ，某视频文件的大小约为 $1 G B, 1 G B$ 等于（）

A、 $2^{30} B$ B、 $8^{30} B$ C、 $8 \times 10^{10} B$ D、 $2 \times 10^{30} B$

查看试题解析
3. 下列各式： $- \frac{1}{5}$ ， a²b² ， $\frac{1}{2} x - 1$ ，－25， $\frac{1}{x}$ ， $\frac{x - y}{2}$ ，a²－2ab＋b².其中单项式的个数有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
4. 若多项式x⁵－(m－2)x^my＋4y⁵是五次三项式，则正整数m可以取（）

A、4 B、1，3，4 C、1，2，3，4 D、2，3，4

查看试题解析
5. 若4x²－2(k－1)x＋9是完全平方式，则k的值为（）

A、±2 B、±5 C、7或－5 D、－7或5

查看试题解析
6. 若 -2a^mb⁴与 5aⁿ⁺²b^2m+n可以合并一项，则mn的值是（）

A、2 B、0 C、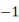 D、1

查看试题解析
7. 要使多项式(x²－px＋2)(x－q)不含x的二次项，则p与q的关系是（）

A、相等 B、互为相反数 C、互为倒数 D、乘积为－1

查看试题解析
8. 计算[(a＋b)²]³·(a＋b)³的结果是（）

A、(a＋b)⁸ B、(a＋b)⁹ C、(a＋b)¹⁰ D、(a＋b)¹¹

查看试题解析
9. 已知a＋b＝m，ab＝－4，则计算(a－1)(b－1)的结果是（）

A、3 B、m C、3－m D、－3－m

查看试题解析
10. 若A＝3x²＋5x＋2，B＝4x²＋5x＋3，则A与B的大小关系是（）

A、A＞B B、A＜B C、A≤B D、无法确定

查看试题解析

二、填空题

11. 计算：（x-2）²-（x+2）（x-2）=.

查看试题解析
12. 已知P=x²+t，Q=2x，若对于任意的实数x，P>Q始终成立，则t的值可以为（写出一个即可）.

查看试题解析
13. 若m，n互为相反数，则3(m－n)－ $\frac{1}{2}$ (2m－10n)＝．

查看试题解析
14. 如果正方形面积是9x²+6xy+y²（x＞0，y＞0），则这个正方形周长是．

查看试题解析
15. 已知n为自然数，代数式x^n＋1－2y³＋1是三次多项式，则n可以取值的个数是个．

查看试题解析

三、计算题

16. 已知x＝156，y＝144，求代数式 $\frac{1}{2}$ x²＋xy＋ $\frac{1}{2}$ y²的值．

查看试题解析
17. 若|x－2|＋x²－xy＋ $\frac{1}{4}$ y²＝0，求x，y的值．

查看试题解析
18. 已知P＝2x²＋4y＋13，Q＝x²－y²＋6x－1，比较代数式P，Q的大小．

查看试题解析

四、解答题

19. 已知a，b为常数，且三个单项式4xy² ， axy^b ，－5xy相加得到的和仍是单项式，求a，b的值．

查看试题解析
20. 若 $- 2 x^{2 m - 1}$ 与 $y^{n - 4}$ 与 $7 x^{1 - n} y^{m - 1}$ 的积与 $x^{7} y^{3}$ 是同类项，求 $m$ 、 $n$ 的值．

查看试题解析
21. 已知 $3 x^{2} + 4 x - 1 = 0$ ，求代数式 ${(2 x + 1)}^{2} - (x + 1) (x - 1)$ 的值．

查看试题解析
22. 发现：当两个不同的正整数同为偶数或奇数时，这两个数之和与这两个数之差的平方差一定能被4整除，且这两个数的积可以表示为两个正整数的平方差．
验证：如， ${(3 + 1)}^{2} - {(3 - 1)}^{2} = 12$ 能被4整除，请把3与1的积写成两个正整数的平方差；

探究：设“发现”中两个正整数分别为m，n，请论证“发现”中的结论正确．

查看试题解析

五、综合题

23.

(1)、计算：- $\sqrt[3]{27}$ +（ $\frac{1}{3}$ ）^-²-cos60°+（π-1）⁰.

(2)、下面是小英化简整式的过程，仔细阅读后解答所提出的问题.
解：x（x+2y）-（x+1）²+2x
=x²+2xy-x²+2x+1+2x                                    第一步
=2xy+4x+1                                              第二步
任务：
小英的化简过程从第一步开始出现错误，应改为；化简的正确结果为.

查看试题解析
24. 现有甲、乙、丙三种矩形卡片各若干张，卡片的边长如图1所示 $(a > 1)$ ．某同学分别用6张卡片拼出了两个矩形(不重叠无缝隙)，如图2和图3，其面积分别为 $S_{1} ， S_{2}$ ．

(1)、请用含a的式子分别表示 $S_{1} ， S_{2}$ ；当 $a = 2$ 时，求 $S_{1} + S_{2}$ 的值；

(2)、比较 $S_{1}$ 与 $S_{2}$ 的大小，并说明理由．

查看试题解析
25. 阅读下面材料：
将边长分别为a， $a + \sqrt{b}$ ， $a + 2 \sqrt{b}$ ， $a + 3 \sqrt{b}$ 的正方形面积分别记为 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ， $S_{4}$ ．

则 $S_{2} - S_{1} = (a + \sqrt{b})^{2} - a^{2}$

      $= [(a + \sqrt{b}) + a] \cdot [(a + \sqrt{b}) - a]$

      $= (2 a + \sqrt{b}) \cdot \sqrt{b}$

      $= b + 2 a \sqrt{b}$

例如：当 $a = 1$ ， $b = 3$ 时， $S_{2} - S_{1} = 3 + 2 \sqrt{3}$

根据以上材料解答下列问题：

(1)、当 $a = 1$ ， $b = 3$ 时， $S_{3} - S_{2} =$ ， $S_{4} - S_{3} =$ ；

(2)、当 $a = 1$ ， $b = 3$ 时，把边长为 $a + n \sqrt{b}$ 的正方形面积记作 $S_{n + 1}$ ，其中n是正整数，从（1）中的计算结果，你能猜出 $S_{n + 1} - S_{n}$ 等于多少吗？并证明你的猜想；

(3)、当 $a = 1$ ， $b = 3$ 时，令 $t_{1} = S_{2} - S_{1}$ ， $t_{2} = S_{3} - S_{2}$ ， $t_{3} = S_{4} - S_{3}$ ， …， $t_{n} = S_{n + 1} - S_{n}$ ，且 $T = t_{1} + t_{2} + t_{3} + ⋯ + t_{50}$ ，求T的值．

查看试题解析