【北师大版·数学】2024年中考一轮复习之平行线的性质
试卷更新日期:2023-12-05 类型:一轮复习
一、选择题
-
1. 如图,直线 , 直线与被直线所截形成的几个角中,与相等的是( )
 A、
A、
B、
C、
D、2. 如图,直线 , 被直线所截, , , 则的度数为( )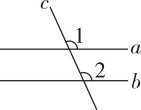 A、 B、 C、 D、3. 如图,直线 , 是截线,的度数是( )
A、 B、 C、 D、3. 如图,直线 , 是截线,的度数是( ) A、
A、
B、
C、
D、4. 如图,直线 , 直线 , 被直线所截,若 , 则为( ) A、 B、 C、 D、5. 如图, , , 若 , 则的度数是( )
A、 B、 C、 D、5. 如图, , , 若 , 则的度数是( )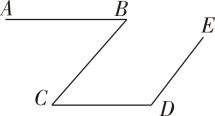 A、
A、
B、
C、
D、6. 如图,直线 , 将含有角的直角三角尺按如图所示的位置放置,若 , 那么的大小为( )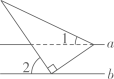 A、 B、 C、 D、7. 下列图形中,由 , 能得到的是( )A、
A、 B、 C、 D、7. 下列图形中,由 , 能得到的是( )A、 B、
B、 C、
C、 D、
D、 8. 山上的一段观光索道如图所示,索道支撑架均为互相平行 , 且每两个支撑架之间的索道均是直的,若 , , 则( )
8. 山上的一段观光索道如图所示,索道支撑架均为互相平行 , 且每两个支撑架之间的索道均是直的,若 , , 则( ) A、 B、 C、 D、9. 如图,中, , 顶点 , 分别在直线 , 上.若 , , 则的度数为( )
A、 B、 C、 D、9. 如图,中, , 顶点 , 分别在直线 , 上.若 , , 则的度数为( ) A、 B、 C、 D、10. 如图,直线 , 菱形和等边在 , 之间,点A,F分别在 , 上,点B,D,E,G在同一直线上:若 , , 则( )
A、 B、 C、 D、10. 如图,直线 , 菱形和等边在 , 之间,点A,F分别在 , 上,点B,D,E,G在同一直线上:若 , , 则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,直线 , 直线l与直线a,b分别相交于A,B两点,过点A作直线l的垂线交直线b于点C,若 , 则的度数为 .
 12. 某些灯具的设计原理与抛物线有关.如图,从点照射到抛物线上的光线 , 等反射后都沿着与平行的方向射出.若 , , 则 .
12. 某些灯具的设计原理与抛物线有关.如图,从点照射到抛物线上的光线 , 等反射后都沿着与平行的方向射出.若 , , 则 . 13. 如图,已知直线 , 的顶点在直线上, , , 则的度数是 .
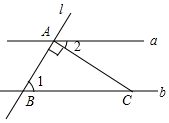
13. 如图,已知直线 , 的顶点在直线上, , , 则的度数是 . 14. 如图,已知直线AB∥CD,∠1=60°,∠2=45°,则∠CBD的度数为 .
14. 如图,已知直线AB∥CD,∠1=60°,∠2=45°,则∠CBD的度数为 . 15. 2022北京冬奥会掀起了滑雪的热潮,谷爱凌的励志故事也激励着我们青少年,很多同学纷纷来到滑雪场,想亲身感受一下奥运健儿在赛场上风驰电掣的感觉,但是第一次走进滑雪场的你,如果不想体验人仰马翻的感觉,学会正确的滑雪姿势是最重要的,正确的滑雪姿势是上身挺直略前倾,与小腿平行,使脚的根部处于微微受力的状态,如图所示,AB//CD,当人脚与地面的夹角∠CDE=60°时,求出此时头顶A与水平线的夹角∠BAF的度数为 .
15. 2022北京冬奥会掀起了滑雪的热潮,谷爱凌的励志故事也激励着我们青少年,很多同学纷纷来到滑雪场,想亲身感受一下奥运健儿在赛场上风驰电掣的感觉,但是第一次走进滑雪场的你,如果不想体验人仰马翻的感觉,学会正确的滑雪姿势是最重要的,正确的滑雪姿势是上身挺直略前倾,与小腿平行,使脚的根部处于微微受力的状态,如图所示,AB//CD,当人脚与地面的夹角∠CDE=60°时,求出此时头顶A与水平线的夹角∠BAF的度数为 .
三、解答题
-
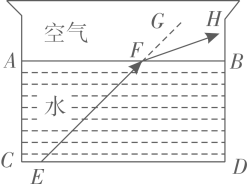
16. 光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射,如图,水面 与水杯下沿 平行,光线 从水中射向空气时发生折射,光线变成 ,点G在射线 上,已知 ,求 的度数.
 17. 如图,已知AB∥CD,EF交AB于点E,交CD于点F,FG平分∠EFD,交AB于点G.若∠1=50°,求∠BGF的度数.
17. 如图,已知AB∥CD,EF交AB于点E,交CD于点F,FG平分∠EFD,交AB于点G.若∠1=50°,求∠BGF的度数. 18. 如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.
18. 如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.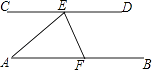 19. 如图,直线a∥b,Rt△ABC的顶点B在直线a上,∠C=90°,∠β=55°,求∠α的度数.
19. 如图,直线a∥b,Rt△ABC的顶点B在直线a上,∠C=90°,∠β=55°,求∠α的度数.
四、综合题
-
20. 如图所示,五边形ABCDE是张大爷十年前承包的一块土地的示意图.经过多年开垦荒地,现已变成如图所示的形状,但承包土地与开垦荒地的分界小路(即图中折线CDE)还保留着,张大爷想过E点修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多,右边的土地面积与开垦的荒地面积一样多.请你用有关的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积)
 (1)、写出设计方案,并在图中画出相应的图形;(2)、说明方案设计理由.21. 如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,∠AMF=90°,∠BAM=30°,AB=6m.
(1)、写出设计方案,并在图中画出相应的图形;(2)、说明方案设计理由.21. 如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,∠AMF=90°,∠BAM=30°,AB=6m.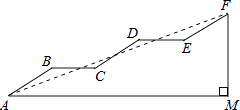 (1)、求FM的长;(2)、连接AF,若sin∠FAM= ,求AM的长.22. 黄岩岛自古以来就是中国的领土,如图,为维护海洋利益,三沙市一艘海监船在黄岩岛附近海域巡航,某一时刻海监船在A处测得该岛上某一目标C在它的北偏东45°方向,海监船以30海里每小时的速度沿北偏西30°方向航行2小时后到达B处,此时测得该目标C在它的南偏东75°方向.求:
(1)、求FM的长;(2)、连接AF,若sin∠FAM= ,求AM的长.22. 黄岩岛自古以来就是中国的领土,如图,为维护海洋利益,三沙市一艘海监船在黄岩岛附近海域巡航,某一时刻海监船在A处测得该岛上某一目标C在它的北偏东45°方向,海监船以30海里每小时的速度沿北偏西30°方向航行2小时后到达B处,此时测得该目标C在它的南偏东75°方向.求: (1)、∠C的度数;(2)、求该船与岛上目标C之间的距离 即CB的长度(结果保留根号)
(1)、∠C的度数;(2)、求该船与岛上目标C之间的距离 即CB的长度(结果保留根号)