新疆阿克苏地区拜城县2023-2024学年八年级上学期数学期中考试试卷
试卷更新日期:2023-12-05 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 要组成一个三角形,三条线段长度可取( ).A、9,6,13 B、15,6,8 C、2,3,5 D、3,5,92. 剪纸艺术是中华民族的瑰宝,下面剪纸作品中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在如图中,正确画出△ABC的边BC上的高的是( )A、
3. 在如图中,正确画出△ABC的边BC上的高的是( )A、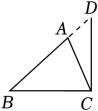 B、
B、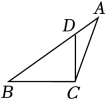 C、
C、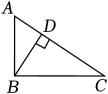 D、
D、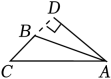 4. 一个三角形三个内角的度数之比为2:3:7,这个三角形一定是( )
4. 一个三角形三个内角的度数之比为2:3:7,这个三角形一定是( )
A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形5. 如图,AB∥CD , ∠ABE=150°,∠BEF=70°,则∠DFE的度数为( ) A、30° B、40° C、50° D、60°6. 一个n边形的内角和比其外角和的2倍多 , 则n的值是( )A、7 B、6 C、5 D、47. 已知点P(2,a)与Q(2,b)关于x轴对称,则a+b=( )A、1 B、0 C、4 D、28. 如图,强强想测量旗杆AB的高度,旗杆对面有一高为18米的大楼CD , 大楼与旗杆相距28米(BD=28米),在大楼前10米的点P处,测得∠APC=90°,且AB⊥BD , CD⊥BD , 则旗杆AB的高为( )
A、30° B、40° C、50° D、60°6. 一个n边形的内角和比其外角和的2倍多 , 则n的值是( )A、7 B、6 C、5 D、47. 已知点P(2,a)与Q(2,b)关于x轴对称,则a+b=( )A、1 B、0 C、4 D、28. 如图,强强想测量旗杆AB的高度,旗杆对面有一高为18米的大楼CD , 大楼与旗杆相距28米(BD=28米),在大楼前10米的点P处,测得∠APC=90°,且AB⊥BD , CD⊥BD , 则旗杆AB的高为( )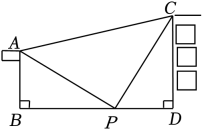 A、8米 B、10米 C、12米 D、18米9. 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,以点A为圆心,适当长为半径画弧,分别交AC , AB于点M , N , 再分别以M , N为圆心,大于的长为半径画弧,两弧在∠CAB的内部相交于点P , 画射线AP与BC交于点D , DE⊥AB , 垂足为E . 则下列结论错误的是( )
A、8米 B、10米 C、12米 D、18米9. 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,以点A为圆心,适当长为半径画弧,分别交AC , AB于点M , N , 再分别以M , N为圆心,大于的长为半径画弧,两弧在∠CAB的内部相交于点P , 画射线AP与BC交于点D , DE⊥AB , 垂足为E . 则下列结论错误的是( )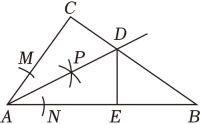 A、∠CAD=∠BAD B、CD=DE C、 D、10. 如图,在△ABC中,∠C=90°,AD平分∠BAC , DE⊥AB于E , 则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB , 其中正确的有( )
A、∠CAD=∠BAD B、CD=DE C、 D、10. 如图,在△ABC中,∠C=90°,AD平分∠BAC , DE⊥AB于E , 则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB , 其中正确的有( )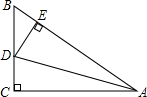 A、2个 B、3个 C、4个 D、1个
A、2个 B、3个 C、4个 D、1个二、填空题(每题3分,共15分)
-
11. 如图,点B、F、C、E在一条直线上,∠A=∠D=90°,AB=DE , 若用“HL”判定△ABC≌△DEF , 则添加的一个条件是 .
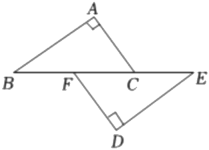 12. 如图,直线AB∥CD , 且AC⊥CB于点C , 若∠BAC=35°,则∠BCD的度数为 .
12. 如图,直线AB∥CD , 且AC⊥CB于点C , 若∠BAC=35°,则∠BCD的度数为 . 13. 如图,五边形ABCDE的一个内角∠A=110°,则∠1+∠2+∠3+∠4等于 .
13. 如图,五边形ABCDE的一个内角∠A=110°,则∠1+∠2+∠3+∠4等于 .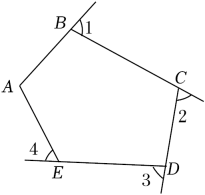 14. 已知点P(a , 2a-3)关于x轴对称的点在第一象限,则a的取值范围是 .15. 如图,在中,AB=AC,BC=4,面积是10.AB的垂直平分线ED分别交AC,AB边于E、D两点,若点F为BC边的中点,点P为线段ED上一动点,则PBF周长的最小值为.
14. 已知点P(a , 2a-3)关于x轴对称的点在第一象限,则a的取值范围是 .15. 如图,在中,AB=AC,BC=4,面积是10.AB的垂直平分线ED分别交AC,AB边于E、D两点,若点F为BC边的中点,点P为线段ED上一动点,则PBF周长的最小值为.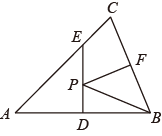
三、解答题(共计55分)
-
16.
近年来,国家实施“村村通”工程和农村医疗卫生改革,某县计划在张村、李村之间建一座定点医疗站P,张、李两村坐落在两相交公路内(如图所示).医疗站必须满足下列条件:①使其到两公路距离相等;②到张、李两村的距离也相等.请你通过作图确定P点的位置.
 17. 如图,在△ABC中,D是BC上的一点,∠1=∠2,∠3=∠4,∠B=40°,求∠BAC的度数.
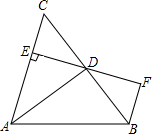
17. 如图,在△ABC中,D是BC上的一点,∠1=∠2,∠3=∠4,∠B=40°,求∠BAC的度数.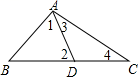 18. 如图所示,AC=AE , ∠1=∠2,AB=AD . 求证:BC=DE .
18. 如图所示,AC=AE , ∠1=∠2,AB=AD . 求证:BC=DE .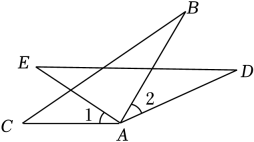 19. 已知:如图,AC∥DF , 点B为线段AC上一点,连接BF交DC于点H , 过点A作AE∥BF分别交DC、DF于点G、点E , DG=CH , 求证:△DFH≌△CAG .
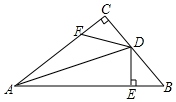
19. 已知:如图,AC∥DF , 点B为线段AC上一点,连接BF交DC于点H , 过点A作AE∥BF分别交DC、DF于点G、点E , DG=CH , 求证:△DFH≌△CAG .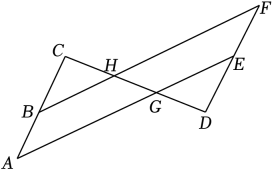 20. 如图,△ABC中,∠C=90°,DE⊥AB于E , F在AC上,且BE=FC , BD=FD , 求证:AD是∠BAC的平分线.
20. 如图,△ABC中,∠C=90°,DE⊥AB于E , F在AC上,且BE=FC , BD=FD , 求证:AD是∠BAC的平分线.