江西省九江市都昌县2023-2024学年八年级上学期期中数学试题
试卷更新日期:2023-12-05 类型:期中考试
一、选择题(每小题3分,共18分)
-
1. 49的平方根是( )A、 B、7 C、 D、2. 下列曲线中能表示 是 的函数的是( )A、
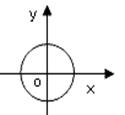 B、
B、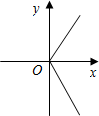 C、
C、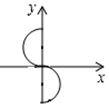 D、
D、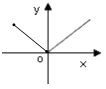 3. 下列各数中,是有理数的是( )A、 B、 C、 D、4. 以下列各组数为边的三角形中,是直角三角形的有( )
3. 下列各数中,是有理数的是( )A、 B、 C、 D、4. 以下列各组数为边的三角形中,是直角三角形的有( )
(1)3,4,5;(2) , , ;(3) , , ;(4)0.03,0.04,0.05.A、1个 B、2个 C、3个 D、4个5. 已知关于x的多项式是一个完全平方式,则一次函数经过的象限是( )A、第一、二、三象限 B、第二、三、四象限 C、第一、二、四象限 D、第一、三、四象限6. 如图,已知圆柱底面的周长为4 dm,圆柱的高为2 dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长的最小值为( )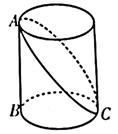 A、 dm B、 dm C、 dm D、 dm
A、 dm B、 dm C、 dm D、 dm二、填空题(每小题3分,共18分)
-
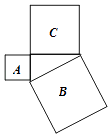
7. 函数 中,自变量 的取值范围是 .8. 已知点在直线上,则点A关于y轴对称的坐标是.9. 对于任意的正数m、n , 定义运算为: , 计算的结果是.10. 已知某一次函数的图象经过点 , , 三点,则a的值是.11. 如图,正方形A、B、C的边长分别为直角三角形的三边长,若正方形A、B的边长分别为3和5,则正方形C的面积为 .
 12. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步 , 先到终点的人原地休息.已知甲先出发.在跑步过程中,甲、乙两人的距离与乙出发的时间之间的关系如图所示,给出以下结论:①;②;③.其中正确的是.
12. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步 , 先到终点的人原地休息.已知甲先出发.在跑步过程中,甲、乙两人的距离与乙出发的时间之间的关系如图所示,给出以下结论:①;②;③.其中正确的是.
三、解答题(第13-17题每题6分,第18-20题每题8分,第21、22题每题9分,第23题12分,共84分)
-
13. 计算题(1)、(2)、14. 已知的立方根是3,的算术平方根是4,c是的整数部分,一个正数的两个平方根分别是和 , 求的平方根.15. 已知一次函数的图象过 , 两点.(1)、求这个一次函数的关系式;(2)、试判断点是否在这个一次函数的图象上.16. 如图所示在正方形网格中,点A的坐标为 , 按要求解答下列问题:
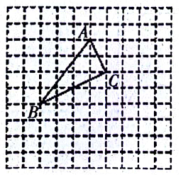 (1)、在图中建立正确的平面直角坐标系,并写出点B , C的坐标;(2)、作出三角形ABC关于x轴的对称图形三角形A'B'C'.(不写作法)17. 已知函数(1)、若函数图象经过原点,求m的值.(2)、若函数的图象平行于直线 , 求m的值.(3)、若这个函数是一次函数,且y随x的增大而减小,m在、、0、1、2这5个数中取值,m的可能取值为?18. 已知:如图,四边形中 , , , 且.试求:
(1)、在图中建立正确的平面直角坐标系,并写出点B , C的坐标;(2)、作出三角形ABC关于x轴的对称图形三角形A'B'C'.(不写作法)17. 已知函数(1)、若函数图象经过原点,求m的值.(2)、若函数的图象平行于直线 , 求m的值.(3)、若这个函数是一次函数,且y随x的增大而减小,m在、、0、1、2这5个数中取值,m的可能取值为?18. 已知:如图,四边形中 , , , 且.试求: (1)、的度数.(2)、四边形的面积(结果保留根号).19. 我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间的有关问题,这种方法称为等面积法,请你用等面积法来探究下列两个问题:
(1)、的度数.(2)、四边形的面积(结果保留根号).19. 我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间的有关问题,这种方法称为等面积法,请你用等面积法来探究下列两个问题: (1)、如图1,著名的赵爽弦图是由四个全等的直角三角形拼成,请你用它验证勾股定理;(2)、如图2,在中, , 是边上高, , , 求的长度.20. 在平面直角坐标系中,一次函数的图象交y轴于点D , 且它与正比例函数的图象交于点 , 设x轴上有一点P , 过点P作x轴的垂线(垂线位于点A的右侧),分别交和的图象与点B、C.
(1)、如图1,著名的赵爽弦图是由四个全等的直角三角形拼成,请你用它验证勾股定理;(2)、如图2,在中, , 是边上高, , , 求的长度.20. 在平面直角坐标系中,一次函数的图象交y轴于点D , 且它与正比例函数的图象交于点 , 设x轴上有一点P , 过点P作x轴的垂线(垂线位于点A的右侧),分别交和的图象与点B、C. (1)、求m和n的值;(2)、若 , 求点P的坐标.21. 已知某服装厂现有布料70米,现计划用这种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用布料1.6米,可获利100元;做一套N型号的时装需用布料0.6米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.(1)、求y(元)与x(套)之间的函数表达式.(2)、当生产M型号的时装多少套时,能使该厂所获利润最大?最大利润是多少?22. 阅读下列解题过程:
(1)、求m和n的值;(2)、若 , 求点P的坐标.21. 已知某服装厂现有布料70米,现计划用这种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用布料1.6米,可获利100元;做一套N型号的时装需用布料0.6米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.(1)、求y(元)与x(套)之间的函数表达式.(2)、当生产M型号的时装多少套时,能使该厂所获利润最大?最大利润是多少?22. 阅读下列解题过程:已知a、b、c为的三边长,且满足 , 试判断的形状.
解:因为 , ①
所以. ②
所以. ③
所以是直角三角形. ④
回答下列问题:
(1)、上述解题过程,从哪一步开始出现错误?该步的序号为;(2)、错误的原因为;(3)、请你将正确的解答过程写下来.23. 如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如 , , , 因此,4,12,20这三个数都是神秘数.(1)、28和52这两个数是神秘数吗?为什么?(2)、设两个连续偶数为和(其中k取非负数),由这两个连续偶数构成的神秘数是4的倍数吗?为什么?(3)、两个连续奇数的平方差(取正数)是神秘数吗?为什么?