河北省石家庄市44中2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2023-12-05 类型:期中考试
一、选择题
-
1. 九(2)班“环保小组”的5位同学在一次活动中捡废弃塑料袋的个数分别为:4,6,8,16,16。这组数据的中位数、众数分别为( )
A、16,16 B、10,16 C、8,8 D、8,162. 甲乙两班的学生在同一次数学测试,两班的平均分都是95分,方差分别为 , , 那么成绩比较整齐的班级是( )A、甲班 B、乙班 C、两班一样整齐 D、无法确定3. 若 ,则 的值为( )A、1 B、 C、 D、4. 如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了2m,此时小球距离地面的高度为( )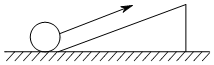 A、5m B、2m C、2m D、m5. 如图,的对角线交于点 , 点为中点,连接交于点 , 若 , 则的长为( )
A、5m B、2m C、2m D、m5. 如图,的对角线交于点 , 点为中点,连接交于点 , 若 , 则的长为( )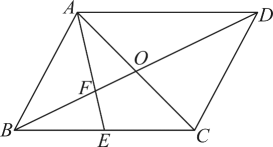 A、 B、3 C、 D、6. 关于x的方程 ,下列结论正确的是( )A、当 时,方程无实数根 B、当 时,方程只有一个实数根 C、当 时,有两个不相等的实数根 D、当 时,方程有两个相等的实数根7. 如图,四边形 是 的内接四边形, ,则 的度数为( )
A、 B、3 C、 D、6. 关于x的方程 ,下列结论正确的是( )A、当 时,方程无实数根 B、当 时,方程只有一个实数根 C、当 时,有两个不相等的实数根 D、当 时,方程有两个相等的实数根7. 如图,四边形 是 的内接四边形, ,则 的度数为( )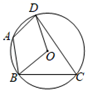 A、 B、 C、 D、8. 比萨斜塔是意大利的著名建筑,其示意图如图所示.设塔顶中心点为点B,塔身中心线 与垂直中心线 的夹角为 ,过点B向垂直中心线 引垂线,垂足为点D.通过测量可得 、 、 的长度,利用测量所得的数据计算 的三角函数值,进而可求 的大小.下列关系式正确的是( )
A、 B、 C、 D、8. 比萨斜塔是意大利的著名建筑,其示意图如图所示.设塔顶中心点为点B,塔身中心线 与垂直中心线 的夹角为 ,过点B向垂直中心线 引垂线,垂足为点D.通过测量可得 、 、 的长度,利用测量所得的数据计算 的三角函数值,进而可求 的大小.下列关系式正确的是( )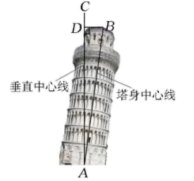 A、 B、 C、 D、9. 如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则 的值为( )
A、 B、 C、 D、9. 如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则 的值为( )
 A、 B、 C、 D、10. 已知反比例函数 ,下列说法中正确的是( )A、该函数的图象分布在第一、三象限 B、点(-4,-3)在函数图象上 C、y随x的增大而增大 D、若点(-2,y1)和(-1,y2)在该函数图象上,则y1<y211. 下表是小红填写的实践活动报告的部分内容,设铁塔顶端到地面的高度为 , 根据以上条件,可以列出的方程为 ( )
A、 B、 C、 D、10. 已知反比例函数 ,下列说法中正确的是( )A、该函数的图象分布在第一、三象限 B、点(-4,-3)在函数图象上 C、y随x的增大而增大 D、若点(-2,y1)和(-1,y2)在该函数图象上,则y1<y211. 下表是小红填写的实践活动报告的部分内容,设铁塔顶端到地面的高度为 , 根据以上条件,可以列出的方程为 ( )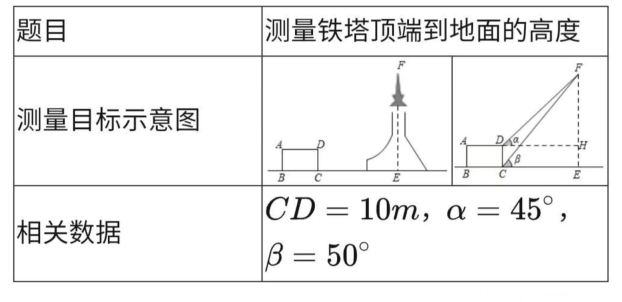 A、 B、 C、 D、12. 在中, , 用直尺和圆规在AB上确定点D , 使 , 根据作图痕迹判断,正确的是( )A、
A、 B、 C、 D、12. 在中, , 用直尺和圆规在AB上确定点D , 使 , 根据作图痕迹判断,正确的是( )A、 B、
B、 C、
C、 D、
D、 13. 函数与在同一直角坐标系中的图像可能是( )A、
13. 函数与在同一直角坐标系中的图像可能是( )A、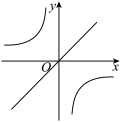 B、
B、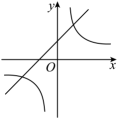 C、
C、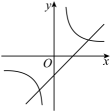 D、
D、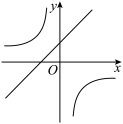 14. 如图,平面直角坐标系中,过点 作 轴于点 ,连接 ,将 绕点 逆时针旋转 , 、 两点的对应点分别为 、 .当双曲线 与 有公共点时, 的取值范围是( )
14. 如图,平面直角坐标系中,过点 作 轴于点 ,连接 ,将 绕点 逆时针旋转 , 、 两点的对应点分别为 、 .当双曲线 与 有公共点时, 的取值范围是( )
 A、 B、 C、 D、15. 有一题目:“已知;点 为 的外心, ,求 .”嘉嘉的解答为:画 以及它的外接圆 ,连接 , ,如图.由 ,得 .而淇淇说:“嘉嘉考虑的不周全, 还应有另一个不同的值.”,下列判断正确的是( )
A、 B、 C、 D、15. 有一题目:“已知;点 为 的外心, ,求 .”嘉嘉的解答为:画 以及它的外接圆 ,连接 , ,如图.由 ,得 .而淇淇说:“嘉嘉考虑的不周全, 还应有另一个不同的值.”,下列判断正确的是( )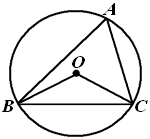 A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得50° D、两人都不对, 应有3个不同值16. 如图,在x轴正半轴上依次截取 , 过点、、、…、、分别作x轴的垂线,与反比例函数的图像依次相交于、、 , …、、 , 得到直角三角形、、…、 , 并设其面积分别为、、…、 , 则的值为( )
A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得50° D、两人都不对, 应有3个不同值16. 如图,在x轴正半轴上依次截取 , 过点、、、…、、分别作x轴的垂线,与反比例函数的图像依次相交于、、 , …、、 , 得到直角三角形、、…、 , 并设其面积分别为、、…、 , 则的值为( )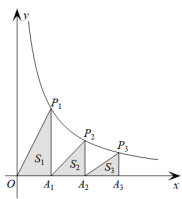 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共12分)
-
17. 若一个直角三角形的两条直角边长分别为7cm和24cm,则这个三角形的外接圆的直径长为cm.18. 若锐角满足 , 求=度19. 如图,已知点坐标为 , 为轴正半轴上一动点,则度数为 , 在点运动的过程中的最小值为 .
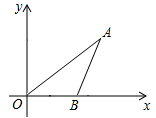
三、解答题(共66分)
-
20. 计算:(1)、(2)、21. 解方程:(1)、-4x+3=0;(2)、;22. 如图,的顶点都在网格点上,点A的坐标为 .
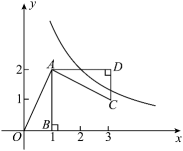
 (1)、以点O为位似中心,把按放大,在y轴的左侧,画出放大后的;(2)、点A的对应点D的坐标是;(3)、 .23. 如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为B , 已知AB=BO=4.反比例函数(k>0,x>0)的图象经过AO的中点C(2,2),交AB于点D .
(1)、以点O为位似中心,把按放大,在y轴的左侧,画出放大后的;(2)、点A的对应点D的坐标是;(3)、 .23. 如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为B , 已知AB=BO=4.反比例函数(k>0,x>0)的图象经过AO的中点C(2,2),交AB于点D .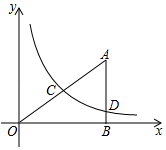 (1)、求反比例函数的表达式;(2)、求经过C、D两点的直线所对应的函数表达式;(3)、设点E是x轴上的动点,请直接写出使△OCE为直角三角形的点E的坐标.24. 图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
(1)、求反比例函数的表达式;(2)、求经过C、D两点的直线所对应的函数表达式;(3)、设点E是x轴上的动点,请直接写出使△OCE为直角三角形的点E的坐标.24. 图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.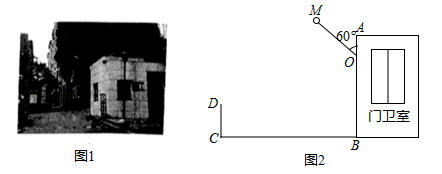 (1)、求点M到地面的距离;(2)、某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据: 1.73,结果精确到0.01米)25. 如图,在平面直角坐标系中,点 , 点分别在轴,轴的正半轴上,且满足 .
(1)、求点M到地面的距离;(2)、某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据: 1.73,结果精确到0.01米)25. 如图,在平面直角坐标系中,点 , 点分别在轴,轴的正半轴上,且满足 . (1)、求点 , 点的坐标.(2)、若点P从C点出发,以每秒1个单位的速度沿线段CB由C向B运动,连接AP , 设的面积为S,点P的运动时间为t秒,求S与t的函数关系式.(3)、在(2)的条件下,是否存在点 , 使以点为顶点的三角形与相似?若存在,请直接写出点的坐标;若不存在,请说明理由.26. 综合与探究
(1)、求点 , 点的坐标.(2)、若点P从C点出发,以每秒1个单位的速度沿线段CB由C向B运动,连接AP , 设的面积为S,点P的运动时间为t秒,求S与t的函数关系式.(3)、在(2)的条件下,是否存在点 , 使以点为顶点的三角形与相似?若存在,请直接写出点的坐标;若不存在,请说明理由.26. 综合与探究如图1,在平面直角坐标系中,菱形的顶点在轴上,反比例函数()的图象经过点 , 并与线段交于点 , 反比例函数()的图象经过点 , 交轴于点 . 已知 .
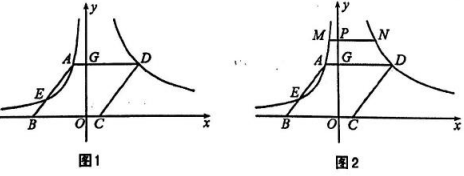 (1)、求点的坐标及反比例函数()的表达式;(2)、直接写出点的坐标 ;(3)、如图2,点是轴正半轴上的一个动点,过点作轴的垂线,分别交反比例函数()与反比例函数()的图象于点 , 设点的坐标为
(1)、求点的坐标及反比例函数()的表达式;(2)、直接写出点的坐标 ;(3)、如图2,点是轴正半轴上的一个动点,过点作轴的垂线,分别交反比例函数()与反比例函数()的图象于点 , 设点的坐标为①当时,求的值;
②在点运动过程中,是否存在某一时刻,使?若存在,直接写出点的坐标;若不存在,说明理由.