河北省石家庄市晋州市2023-2024学年九年级上学期期中考试数学试卷
试卷更新日期:2023-12-05 类型:期中考试
一、选择题(本大题共16个小题,共38分.1~6小题各3分;7~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 把一元二次方程化成一般形式后,若二次项系数为2,则一次项系数和常数项分别是( )A、 , B、 , C、 , D、 ,2. 一元二次方程的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定3. 把方程转化成的形式,则m , n的值是( )A、 , B、 , C、 , D、 ,4. 甲、乙两人在相同条件下,各射击10次,经计算,甲射击成绩的平均数是8环,方差是1.2环;乙射击成绩的平均数是8环,方差是1.6环.下列说法不一定正确的是( )A、甲、乙成绩的总环数相同 B、甲的成绩比乙的成绩稳定 C、甲、乙成绩的中位数可能相同 D、甲、乙成绩的众数一定相同5. 若数据2,3,4,5,6,x存在唯一众数,且该组数据的平均数等于众数,则x的值为( )A、2 B、3 C、4 D、56. 如图,在矩形中,若 , , , 则的长为( )
 A、2 B、4 C、6 D、7.57. 如图,一壁厚均匀的容器外径为18 , 用一个交叉卡钳(两条尺长和相等)可测量容器的内部直径.如果 , 且量得 , 则零件的厚度x为( )
A、2 B、4 C、6 D、7.57. 如图,一壁厚均匀的容器外径为18 , 用一个交叉卡钳(两条尺长和相等)可测量容器的内部直径.如果 , 且量得 , 则零件的厚度x为( ) A、0.25 B、0.3 C、0.35 D、0.48. 如图所示,是一座建筑物的截面图,高 , 坡面的坡度为 , 则斜坡的长度为( )
A、0.25 B、0.3 C、0.35 D、0.48. 如图所示,是一座建筑物的截面图,高 , 坡面的坡度为 , 则斜坡的长度为( ) A、16m B、m C、m D、m9. 某厂家今年一月份的口罩产量是50万个,三月份的口罩产量是80万个,若设该厂家一月份到三月份口罩产量的月平均增长率为x , 则所列方程为( )A、 B、 C、 D、10. 如图所示,四边形和是以点O为位似中心的位似图形.若 , 四边形的面积是3,则四边形的面积是( )
A、16m B、m C、m D、m9. 某厂家今年一月份的口罩产量是50万个,三月份的口罩产量是80万个,若设该厂家一月份到三月份口罩产量的月平均增长率为x , 则所列方程为( )A、 B、 C、 D、10. 如图所示,四边形和是以点O为位似中心的位似图形.若 , 四边形的面积是3,则四边形的面积是( ) A、9 B、12 C、27 D、4811. 如图所示,在平面直角坐标系中有A , B , C , D四个点,其中恰有三点在反比例函数的图象上,根据图中四点的位置,判断这四个点中不在函数的图象上的点是( )
A、9 B、12 C、27 D、4811. 如图所示,在平面直角坐标系中有A , B , C , D四个点,其中恰有三点在反比例函数的图象上,根据图中四点的位置,判断这四个点中不在函数的图象上的点是( ) A、点A B、点B C、点C D、点D12. 如图所示,把两张矩形纸条交叉叠放在一起,重合部分构成一个四边形 . 固定一张纸条,另一张纸条在转动过程中,下列结论一定成立的是( )
A、点A B、点B C、点C D、点D12. 如图所示,把两张矩形纸条交叉叠放在一起,重合部分构成一个四边形 . 固定一张纸条,另一张纸条在转动过程中,下列结论一定成立的是( ) A、四边形的周长不变 B、四边形的面积不变 C、 D、13. 骐骥中学规定,学生的学期体育成绩满分为100,其中体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.若嘉淇同学的三项成绩(百分制)依次是96分,92分,97分,则嘉淇这学期的体育成绩是( )A、95分 B、95.1分 C、95.2分 D、95.3分14. 在同一平面直角坐标系中,函数与(其中m , n是常数,)的大致图象可能是( )A、
A、四边形的周长不变 B、四边形的面积不变 C、 D、13. 骐骥中学规定,学生的学期体育成绩满分为100,其中体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.若嘉淇同学的三项成绩(百分制)依次是96分,92分,97分,则嘉淇这学期的体育成绩是( )A、95分 B、95.1分 C、95.2分 D、95.3分14. 在同一平面直角坐标系中,函数与(其中m , n是常数,)的大致图象可能是( )A、 B、
B、 C、
C、 D、
D、 15. 如图,坡角为的斜坡上有一棵大树(垂直于水平地面),当太阳光线与水平线成角沿斜坡照下时,在斜坡上树影的长为30米,则大树的高为( )
15. 如图,坡角为的斜坡上有一棵大树(垂直于水平地面),当太阳光线与水平线成角沿斜坡照下时,在斜坡上树影的长为30米,则大树的高为( )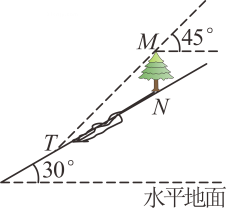 A、米 B、米 C、米 D、米16. 如图所示,在中, , 点P在边上(点P不与B , C重合,且 , 将沿翻折变为 , 交于点M , 交于点N.则下列结论中,不一定正确的是( )
A、米 B、米 C、米 D、米16. 如图所示,在中, , 点P在边上(点P不与B , C重合,且 , 将沿翻折变为 , 交于点M , 交于点N.则下列结论中,不一定正确的是( ) A、平分 B、 C、 D、
A、平分 B、 C、 D、二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分.请把答案写在题目中的横线上)
-
17. 古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔塔顶A的影子处直立一根木杆 , 借助太阳光测金字塔的高度.如图所示,木杆长2米.它的影长是3米,同一时刻测得是201米,则金字塔的高度是米.
 18. 如果关于x的方程的一个根是 , 则k= , 方程的另一个根是 .19. 如图,在平面直角坐标系中,点O为坐标原点,的顶点在双曲线上,顶点B在双曲线 , 且上,边在x轴上.
18. 如果关于x的方程的一个根是 , 则k= , 方程的另一个根是 .19. 如图,在平面直角坐标系中,点O为坐标原点,的顶点在双曲线上,顶点B在双曲线 , 且上,边在x轴上.
①若 , 则的长度为;
②若的面积是7,则k的值是 .
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
20.(1)、计算: .(2)、解方程: .21. 已知 , , 是的三边长,且 .(1)、求的值;(2)、若的周长为81,求三边 , , 的长.22. 骐骥中学举办国庆歌咏比赛,共有十位评委老师现场打分.赛后,对嘉嘉、淇淇和欧欧三位参赛同学得分的数据进行整理、描述和分析.下面给出了部分信息:

①嘉嘉和淇淇两位同学10个得分的折线图
②欧欧10个得分的数据(单位:分):
10,10,9,9,9,7,4,9,10,8.
③三位同学10个得分的平均数
根据以上信息,回答下列问题:
(1)、求表中的m是多少?(2)、嘉嘉同学10个得分的中位数是分,欧欧同学10个得分的众数是分;(3)、对于参赛同学,若某位同学10个得分数据的方差越小,则认为评委对该同学参赛的评价越一致.通过观察折线图或做相关计算,可以推断:在嘉嘉和淇淇两位同学中,评委老师们对的评价更为一致;(4)、如果把每位同学的10个得分先去掉一个最高分和一个最低分,再取剩余8个得分的平均分,最后得分越高,就认为该同学表现越优秀,据此推断:在嘉嘉、淇淇和欧欧三位同学中,表现最优秀的是 .23. 如图所示,点B在的边上(点B不与点O , C重合),连接 , 设 , , . 已知 . (1)、①若 , , 则c=;
(1)、①若 , , 则c=;②若 , 则=;
(2)、求证:关于x的方程必有两个不相等的实数根.24. 如图所示,矩形中, , , 以点O为圆心作半径的圆,交于点D , 点P在线段上,过点P作 , 交圆于两点M , N , 连接 , 的延长线交于点Q . 设(). (1)、当时,=;(2)、在从减少到的过程中,求点Q下降的高度;(3)、设的中点为E , 当点Q在线段上时,请直接写出t的取值范围.25. 如图,在矩形中, , t为正数,点E是的中点,点P是线段上的一个动点(不与点A重合),点Q是的延长线上的一个动点(不与点C重合),且 , 连接 , , 与交于点O . 设 , 的面积为 , 的面积为 , 并设 .
(1)、当时,=;(2)、在从减少到的过程中,求点Q下降的高度;(3)、设的中点为E , 当点Q在线段上时,请直接写出t的取值范围.25. 如图,在矩形中, , t为正数,点E是的中点,点P是线段上的一个动点(不与点A重合),点Q是的延长线上的一个动点(不与点C重合),且 , 连接 , , 与交于点O . 设 , 的面积为 , 的面积为 , 并设 . (1)、嘉淇认为,能用含有x的式子表示S , 她的推理过程如下,请你补充完整:
(1)、嘉淇认为,能用含有x的式子表示S , 她的推理过程如下,请你补充完整:∵ ,
且 ▲ (用含x和t的式子表示),
▲ (用含x和t的式子表示),
∴ ▲ (用含x的式子表示).
(2)、若 , 当时,求的长度(即x的值);(3)、若 , 请结合t值的不同范围,写出的长度是多少?(结合表格进行分析,直接填写表格下面的三个空即可)① ▲ ;②▲1处填写: ▲ ;③▲2处填写: ▲ .
26. 数学课上,老师给出题目:如图所示,在中 , , 点D , E分别是边和边上的动点,且 , 连接 , . 请探究是否存在最小值?并说明理由.嘉淇的想法是把和转移到某处,并使它们“接在一起”,然后利用“两点之间,线段最短”尝试探索,并成功解决了问题.以下是她的探索思路,请你按要求补充具体解题过程.
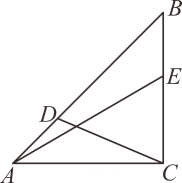 (1)、在射线上取点F , 使 , 把绕点A顺时针旋转,使点D落在点F处,点C落在点G处.
(1)、在射线上取点F , 使 , 把绕点A顺时针旋转,使点D落在点F处,点C落在点G处.①请你运用尺规作图(保留作图痕迹,不用给出证明),作出 , 并连接;
②求证: .
(2)、在(1)的基础上,请你通过探索,求出的最小值,并直接写出此时的长度.