河北省石家庄市平山县2023-2024学年七年级上学期数学期中考试试卷

试卷更新日期：2023-12-05 类型：期中考试

进入出卷网下载

一、选择题（本大题有16个小题，每小题3分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1. $\frac{1}{2}$ 是 $- 2$ 的（）

A、相反数 B、绝对值 C、倒数 D、以上都不对

查看试题解析
2. 某种速冻水饺的储藏温度是 $- 18 \pm 2 ℃$ ，四个冷藏室的温度如下，则不适合储藏此种水饺是（）

A、 $- 17 ℃$ B、 $- 22 ℃$ C、 $- 18 ℃$ D、 $- 19 ℃$

查看试题解析
3. 根据国家统计局发布的统计公报，2022年我国新能源汽车产量7003000辆，其中7003000用科学记数法表示为（）

A、 $70.03 \times 1 0^{5}$ B、 $7.003 \times 1 0^{5}$ C、 $7.003 \times 1 0^{6}$ D、 $0.7003 \times 1 0^{7}$

查看试题解析
4. 已知13.5亿是由四舍五入取得的近似数，它精确到（）

A、十分位 B、千万位 C、亿位 D、十亿位

查看试题解析
5. 下列说法不正确的是（）

A、 $- (- 1) = | - 1 |$ B、最大的负整数是 $- 1$ C、 ${(- 2)}^{3} = - 2^{3}$ D、有理数分为正数和负数

查看试题解析
6. 若 $x = 2$ 是关于 $x$ 的一元一次方程 $2 x + a = 3$ 的解，则 $a$ 的值为（）

A、1 B、 $- 1$ C、7 D、 $- 7$

查看试题解析
7. ${(- 1)}^{2 n} + {(- 1)}^{2 n + 1}$ 的结果为（ $n$ 为正整数）（）

A、0 B、 $- 2$ C、2 D、1

查看试题解析
8. 下列关于0的说法中错误的是（）

A、0是绝对值最小的数 B、0的相反数是0 C、0是整数 D、0的倒数是0

查看试题解析
9. 下列等式变形正确的是（）

A、如果 $2 x = - 2$ ，那么 $x = - 1$ B、如果 $3 a - 2 = 5 a$ ，那么 $3 a + 5 a = 2$ C、如果 $a = b$ ，那么 $a + 1 = b - 1$ D、如果 $6 x = 3$ ，那么 $x = 2$

查看试题解析
10. 已知 $x^{3 - 2 m} y^{2}$ 与 $2 x y^{n}$ 是同类项，则 $m - n$ （）

A、 $- 1$ B、0 C、1 D、2

查看试题解析
11. 若两个非零有理数 $a ， b$ ，满足 $| a | = a ， | b | = - b ， a + b < 0$ ，则 $a ， b$ 的取值符合题意的是（）

A、 $a = 2 ， b = - 1$ B、 $a = - 2 ， b = 1$ C、 $a = 1 ， b = - 2$ D、 $a = - 1 ， b = - 2$

查看试题解析
12. 如图1为2023年8月份的日历表，某同学任意框出了其中的四个数字，如图2，若用 $m$ 表示框图中相应位置的数字，则“？”位置的数字可表示为（）

A、 $m + 1$ B、 $m + 5$ C、 $m + 6$ D、 $m + 7$

查看试题解析
13. 《九章算术》是我国古代数学名著，卷七“盈不足”中有题译文如下：今有人合伙买羊，每人出5钱，会差45钱；每人出7钱，会差3钱.问合伙人数、羊价各是多少？设合伙人数为 $x$ 人，所列方程正确的是（）

A、 $5 x - 45 = 7 x - 3$ B、 $5 x + 45 = 7 x + 3$ C、 $\frac{x + 45}{5} = \frac{x + 3}{7}$ D、 $\frac{x - 45}{5} = \frac{x - 3}{7}$

查看试题解析
14. 如图，数轴上A，B两点分别对应实数a，b，则下列结论正确的是（）

A、 $a + b > 0$ B、 $a b > 0$ C、 $a - b > 0$ D、 $| a | - | b | > 0$

查看试题解析
15. $126 \times 3^{8} = p$ 若，则 $126 \times 3^{6}$ 的值可以表示为（）

A、 $\frac{1}{6} p$ B、 $p - 9$ C、 $p - 6$ D、 $\frac{1}{9} p$

查看试题解析
16. 观察下列图形：它们是按一定规律排列的，依照此规律，第 $n$ （ $n$ 为正整数）个图形中的点数是（）

A、 $6 n - 1$ B、 $6 n + 4$ C、 $5 n - 1$ D、 $5 n + 4$

查看试题解析

二、填空题（本大题有3个小题，共12分．17小题每空1分；18、19小题每空2分）

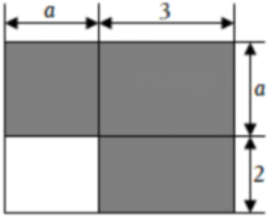
17. 计算下列各题：

(1)、 $- (- 2) =$

(2)、 $- 6 + 6 =$

(3)、 $(- 3) \times 5 =$

(4)、 $2 x - 3 x =$

查看试题解析
18. 如图是一所住宅的建筑平面图（长度单位： $m$ ），这所住宅的建筑面积（阴影部分）为（用含 $a$ 的式子表示），面积的表达式是二次项式．

查看试题解析
19. 下列是一些两位数减法运算：
$21 - 12 = 9 ， 31 - 13 = 18 ， 32 - 23 = 9 ， 42 - 24 = 18$ ，
$14 - 41 = - 27 ， 51 - 15 = 36 ， 26 - 62 = - 36 ， \cdot \cdot \cdot$
观察上述算式及其计算结果，对两位数减法运算中的某种特殊情形进行探究：

(1)、请另外写出一个符合上述规律的算式：；

(2)、用字母表示你所观察到的规律．

查看试题解析

三、解答题（本大题6个小题，共60分．解答应写出文字说明、证明过程或演算步骤）

20. 在数轴上表示下列各数，并按从小到大的顺序用“ $<$ ”号把这些数连接起来： $2 ， - \frac{7}{2} ， 0$ ， $- \frac{4}{3} ， - | - 2.5 | ， \frac{9}{2}$ ．

查看试题解析
21. 计算题：

(1)、 $- 15 + (- 23) - 26 - (- 15)$

(2)、 $(- \frac{1}{2} + \frac{2}{3} - \frac{1}{4}) \times (- 24)$

(3)、 $- 24 \div (- 6) \times (- \frac{1}{4})$

(4)、 $- 1^{2024} - {(- 2)}^{3} - 3^{2} + 2 \div \frac{2}{3} \times \frac{3}{2}$

查看试题解析
22. 先化简，再求值：已知 $a = 2 ， b = - 3$ ，求 $10 a^{2} b - [2 a b^{2} - 2 (a b - 5 a^{2} b)]$ 的值．

查看试题解析
23. 黄老师要在周五开设羽毛球社团，她计划购买16支羽毛球拍和 $x$ 盒羽毛球（ $x > 16$ ）．黄老师发现在学校附近有甲、乙两家商店都在出售相同品牌的羽毛球拍和羽毛球，羽毛球拍每支售价150元，羽毛球每盒售价40元．经过老师的洽谈，甲商店给出每买一支羽毛球拍送一盒羽毛球的优惠；乙商店给出羽毛球拍和羽毛球全部八折的优惠．

(1)、黄老师购买球拍和羽毛球，在甲、乙两家商店付款分别为 $y_{甲} ， y_{乙}$ 元，请用含 $x$ 的式子表示出 $y_{甲} 、 y_{乙}$ ．

(2)、当 $x = 25$ 时，请问黄老师购买这些球拍和羽毛球，在哪个商店更合算？请说明理由．

查看试题解析
24. 已知： $b$ 是最小的正整数，且 $a 、 b$ 满足 ${(c - 6)}^{2} + | a + b | = 0$ ，请回答问题：

(1)、请直接写出 $a 、 b 、 c$ 的值． $a =$ ， $b =$ ， $c =$ ；

(2)、如图， $a 、 b 、 c$ 所对应的点分别为 $A 、 B 、 C$ ，点 $P$ 为一动点，其对应的数为 $x$ ，点 $P$ 在 $A 、 B$ 之间运动时，请化简式子： $| x + 1 | - | x - 1 | - 2 | x + 5 |$ （写出化简过程）

(3)、在（1）（2）的条件下，点 $A 、 B 、 C$ 开始在数牰上运动，若点 $A$ 以每秒 $n (n > 0)$ 个单位长度的速度向左运动，同时，点 $B$ 和点 $C$ 分别以每秒 $2 n$ 个单位长度和 $5 n$ 个单位长度的速度向右运动，假设经过 $t$ 秒钟过后，若点 $B$ 与点 $C$ 之间的距离表示为 $B C$ ，点 $A$ 与点 $B$ 之间的距离表示为 $A B$ ．请问： $B C - A B$ 的值是否随着时间 $t$ 的变化而改变？若变化，请说明理由；若不变，请求其值．

查看试题解析
25. 某学校给学生编制的“身份识别条形码”共有12位数字（均为0～9之间的自然数），它是由11位数字代码和最后1位的校验码构成，具体结构如下图：
其中校验码是按照特定的算法计算得来的，用于校验身份识别条形码中前11位数字代码的正确性．具体算法说明如下：
步骤1：计算前11位数字中奇数位数字的和，记为 $m$ ；
步骤2：计算前11位数字中偶数位数字的和，记为 $n$ ；
步骤3：计算 $3 m + n$ ，记为 $p$ ；
步骤4：取不小于 $p$ 且为10的整数倍的最小数 $q$ ；
步骤5：计算 $q - p$ ，结果即为校验码．
阅读上述材料，回答下列问题：

(1)、某同学的“身份识别条形码”为的 $04220220133 □$ ，则计算过程中 $p$ 的值为．校验码 $□$ 的值是．

(2)、如图，某同学的“身份识别条形码”中的一位数字不小心污损了，设这个数字为 $x$ ，你能否通过其他信息还原出这位数字 $x$ ，进而确定这位同学的班级？如果能，写出你的推理过程，如果不能，说明理由．

(3)、如图，一名2024届的同学在知道了校验码的计算方法后，尝试利用自己的身份信息计算校验码，然后惊喜的发现自己的“班级”、“学号”和“校验码”的数字（图中被遮住的数字）是完全一样的，请直接写出这个数字是．

查看试题解析