（第一次学期同步）第2章有理数的运算—2023-2024学年浙教版七年级数学

试卷更新日期：2023-12-05 类型：单元试卷

进入出卷网下载

一、选择题

1. $- \frac{1}{2023}$ 的倒数是（）

A、2023 B、 $\frac{1}{2023}$ C、 $- 2023$ D、 $- \frac{1}{2022}$

查看试题解析
2. 刘慈欣科幻巨作《三体》中所描述的三体文明距地球大约42000000光年，它们之间被大量氢气和暗物质纽带连接，看起来似乎是连在一起的“三体星系”.其中数字42000000用科学记数法表示为（）

A、 $4.2 \times 1 0^{7}$ B、 $4.2 × 1 0^{6}$ C、 $0.42 \times 1 0^{8}$ D、 $4200 \times 1 0^{4}$

查看试题解析
3. 下列计算结果是负数的是（）．

A、 $- (- \frac{1}{2})$ B、 $| - 2022 |$ C、 ${(- 2)}^{2}$ D、 ${(- 1)}^{3}$

查看试题解析
4. 在 $- (- 2)$ ， $- (- 2)^{2}$ ， ${(- \frac{1}{3})}^{4}$ ， $- (- 1)^{2023}$ ， $- | - 2 |$ 中，正数的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
5. 右图是“大润发”超市中“飘柔”洗发水的价格标签，一服务员不小心将墨水滴在标签上，使得原价看不清楚，该洗发水的原价为（）

A、22元 B、23元 C、24元 D、26元

查看试题解析
6. 某市星期一到星期五的每日最高气温与最低气温的变化趋势图如图，根据图中信息，下列说法正确的是（）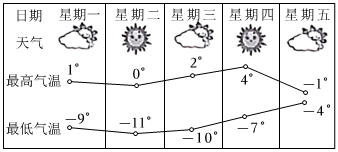

A、星期一的日温差最大 B、星期三的日温差最小 C、星期二与星期四的日温差相同 D、星期一的日温差是星期五日温差的 $2$ 倍

查看试题解析
7. 已知|a|＝2，（b＋1）²＝25，且a＜b，则a＋b的值是（）

A、-2或-8 B、-8或6 C、2或6 D、2或-8

查看试题解析
8. 计算 $\frac{\overset{m 个 3}{\overset{︷}{3 \times 3 \times \cdot \cdot \cdot \times 3}}}{\underset{n 个 2}{\underset{︸}{2 + 2 + \cdot \cdot \cdot + 2}}} =$ （）

A、 $\frac{3 m}{2^{n}}$ B、 $\frac{3^{m}}{2 n}$ C、 $\frac{3 m}{n^{2}}$ D、 $\frac{m^{3}}{2 n}$

查看试题解析
9. 四个互不相等的整数 $a 、 b 、 c 、 d$ ，它们的积 $a b c d = 9$ ，那么 $a + b + c + d$ 等于（）

A、0 B、8 C、-8 D、 $\pm 8$

查看试题解析
10. 求 $1 + 2 + 2^{2} + 2^{3} + ⋯ + 2^{2021}$ 的值，可令 $S = 1 + 2 + 2^{2} + 2^{3} + ⋯ + 2^{2021}$ ，则 $2 S = 2 + 2^{2} + 2^{3} + 2^{4} + ⋯ + 2^{2022}$ ，因此 $2 S - S = 2^{2022} - 1$ ．
仿照以上推理，计算出 $1 + 2021 + 202 1^{2} + 202 1^{3} + ⋯ + 202 1^{2021}$ 的值为（）．

A、 $\frac{202 1^{2022} - 1}{2020}$ B、 $\frac{202 1^{2021} - 1}{2020}$ C、 $\frac{202 1^{2022} - 1}{2021}$ D、 $\frac{202 1^{2022} - 1}{2022}$

查看试题解析

二、填空题

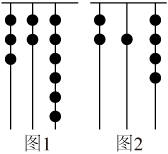
11. 若a，b互为相反数，则 ${(a + b)}^{2} =$ ．

查看试题解析
12. $79.58 \approx$ .（精确到十分位）

查看试题解析
13. 已知 $a$ 的相反数是 $1 \frac{2}{3}$ ， $b$ 的倒数是 $- 2 \frac{1}{2}$ ，则 $a b =$ ．

查看试题解析
14. 我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳记数”.如图一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，如图1，孩子出生后的天数＝3×7²＋2×7¹＋6＝147＋14＋6＝167（天）.请根据图2，计算孩子自出生后的天数是天.

查看试题解析
15. 如图所示是计算机某计算程序，若开始输入x＝4，则最后输出的结果是．

查看试题解析
16. 下列说法：①整数和分数统称为有理数；② $| a | - a \leq 0$ ；③倒数等于它本身的数只有 $\pm 1$ ；④ $- \frac{2^{5}}{3}$ 的底数为 $\frac{2}{3}$ ；⑤20200精确到千位为 $2 \times 1 0^{4}$ ；⑥若 $a b c > 0$ ，则 $\frac{| a |}{a} + \frac{b}{| b |} + \frac{| c |}{c} = 3$ 或 $- 1$ .其中一定正确的是（只需填写序号）.

查看试题解析

三、解答题

17. 计算

(1)、－5²＋（－7）×（－9）－16＋（－2）³

(2)、 $\frac{3}{2} \times (- 8) - \frac{1}{2} \times [- \frac{2}{3} - {(- 2)}^{2}]$

查看试题解析
18. 若a、b互为相反数，c、d互为倒数，m的绝对值为2.求 $m + c d + \frac{a + b}{m}$ 的值.

查看试题解析
19. “低碳生活”从现在做起，从我做起，据测算， $1$ 公顷落叶阔叶林每年可吸收二氧化碳 $14$ 吨，如果每台空调制冷温度在国家提倡的 $26$ 摄氏度基础上调到 $27$ 摄氏度，相应每年减排二氧化碳 $21$ 千克 $.$ 某市仅此项就大约减排相当于 $18000$ 公顷落叶阔叶林全年吸收的二氧化碳，若每个家庭按 $2$ 台空调计算，该市约有多少万户家庭？

查看试题解析
20. 小刚与小明在玩数字游戏，现有5张写着不同数字的卡片（如图），小刚请小明按要求抽出卡片，完成下列各问题：

(1)、从中取出2张卡片，使这2张卡片上的数字乘积最大，如何抽取？最大值是多少？

(2)、从中取出2张卡片，使这2张卡片上的数字相除的商最小，如何抽取？最小值是多少？

查看试题解析
21. 某种茶叶，若直接销售，每千克可获利润12元；若粗加工后销售，每千克可获利润50元；若精加工后销售，每千克可获利润75元．某茶叶加工厂现有这种茶叶140千克，该工厂的生产能力是：如果进行粗加工，每天可加工16千克；如果进行精加工，每天可加工6千克，但两种加工方式不能同时进行．受各种条件限制，工厂必须在15天内（含15天）将这批茶叶全部销售或加工完毕，为此该工厂营销科设计了三种方案：
方案一：全部进行粗加工；
方案二：15天全部进行精加工，没有来得及进行精加工的利润；
方案三：将60千克进行精加工，其余的进行粗加工．
你认为选择哪种方案可获利润最多，为什么？最多可获利润多少元？

查看试题解析
22. 今年以来，由于受国际天然气形势的影响，我国天然气市场总体呈现量紧价高的态势，为确保天然气保供稳价，提高居民生活用气的保障，某地决定从今年 $11$ 月开始调整居民用气价格，调整前后价格如下表（每月用气量为 $a$ 立方米）：

用气类别

第一档（ $0 < a \leq 60$ ）
第二档（ $60 < a \leq 80$ ）
第三档（ $a > 80$ ）
调整前
$2.60$
$2.90$
$3.65$
调整后
$2.95$
$3.25$
$4.10$
注：该地天然气收费按月实行阶梯收费

(1)、某用户 $10$ 月（调整前）缴天然气费 $91$ 元，求该用户这月用气量；

(2)、若该用户 $11$ 月（调整后）用气量与 $10$ 月相同，则该用户 $11$ 月比 $10$ 月多缴费多少元？

(3)、因天气转冷，该用户今年 $12$ 月因取暖用气量急剧增加，缴天然气费 $283$ 元，该用户今年 $12$ 月用气量是多少立方米？

查看试题解析
23. 在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答问题.
（提出问题）三个有理数a，b，c满足 $a b c > 0$ ，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值.

（解决问题）解：由题意，得a，b，c三个有理数都为正数或其中一个为正数，另两个为负数.

①a，b，c都是正数，即 $a > 0$ ， $b > 0$ ， $c > 0$ 时，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = \frac{a}{a} + \frac{b}{b} + \frac{c}{c} = 1 + 1 + 1 = 3$ ；

②当a，b，c中有一个为正数，另两个为负数时，不妨设 $a > 0$ ， $b < 0$ ， $c < 0$ ，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} =$ $\frac{a}{a} + \frac{- b}{b} + \frac{- c}{c} = 1 + (- 1) + (- 1) = - 1$ ，综上所述， $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 值为3或−1.

（探究）请根据上面的解题思路解答下面的问题：

(1)、三个有理数a，b，c满足 $a b c < 0$ ，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值；

(2)、若a，b，c为三个不为0的有理数，且 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = 1$ ，求 $\frac{a b c}{| a b c |}$ 的值.

查看试题解析

	用气类别
	第一档（ $0 < a \leq 60$ ）	第二档（ $60 < a \leq 80$ ）	第三档（ $a > 80$ ）
调整前	$2.60$	$2.90$	$3.65$
调整后	$2.95$	$3.25$	$4.10$

（第一次学期同步） 第2章 有理数的运算—2023-2024学年浙教版七年级数学

一、选择题

二、填空题

三、解答题

（第一次学期同步）第2章有理数的运算—2023-2024学年浙教版七年级数学