(第一次学期单元测试) 第6章 图形的初步认识—2023-2024学年浙教版七年级数学
试卷更新日期:2023-12-04 类型:单元试卷
一、选择题
-
1. 下列各图中,两线能相交的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中,有曲面的几何图形有( )
2. 下列图形中,有曲面的几何图形有( ) A、1个 B、2个 C、3个 D、4个3. 在下列各图形中,∠1和∠2是对顶角的图形是( )A、
A、1个 B、2个 C、3个 D、4个3. 在下列各图形中,∠1和∠2是对顶角的图形是( )A、 B、
B、 C、
C、 D、
D、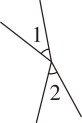 4. 开学第一节课赵老师给每人发了一个正方体,它的六个面分别标注有“一切皆有可能”,表面展开后如图那么在原正方体中,“一”的对面是( )
4. 开学第一节课赵老师给每人发了一个正方体,它的六个面分别标注有“一切皆有可能”,表面展开后如图那么在原正方体中,“一”的对面是( )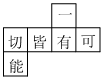 A、能 B、可 C、皆 D、切5. 开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为( )A、两点之间,线段最短 B、经过一点有无数条直线 C、两点确定一条直线 D、两点之间线段的长度,叫做这两点之间的距离6. 如图,在△ABC中,∠ACB=90°,CE是△ABC的角平分线,则∠ACE( )
A、能 B、可 C、皆 D、切5. 开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为( )A、两点之间,线段最短 B、经过一点有无数条直线 C、两点确定一条直线 D、两点之间线段的长度,叫做这两点之间的距离6. 如图,在△ABC中,∠ACB=90°,CE是△ABC的角平分线,则∠ACE( )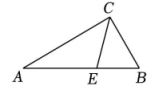 A、50° B、45° C、60° D、65°7. 如图,直线 , 交于点射线平分 , 若 , 则等于( )
A、50° B、45° C、60° D、65°7. 如图,直线 , 交于点射线平分 , 若 , 则等于( ) A、 B、 C、 D、8. 如图是一台起重机的工作简图,前后两次吊杆位置 , 与线绳线绳垂直于地面的夹角分别是和 , 则吊杆前后两次的夹角的度数为( )
A、 B、 C、 D、8. 如图是一台起重机的工作简图,前后两次吊杆位置 , 与线绳线绳垂直于地面的夹角分别是和 , 则吊杆前后两次的夹角的度数为( )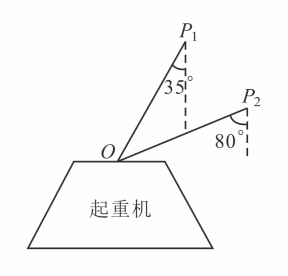 A、 B、 C、 D、9. 下列说法:
A、 B、 C、 D、9. 下列说法:正数和负数统称为有理数;若 , 则、互为相反数;如果 , 则有;如果两个角的和等于 , 我们就说这两个角互余;有理数的倒数是 .
其中正确的有( )
A、个 B、个 C、个 D、个10. 如图,C、D是线段AB上两点,M、N分别是线段AD,BC的中点,下列结论:①若AD=BM,则AB=3BD;②AC=BD,则AM=BN;③AC﹣BD=2(MC﹣DN);④2MN=AB﹣CD.
其中正确的结论是( )
 A、①②③ B、③④ C、①②④ D、①②③④
A、①②③ B、③④ C、①②④ D、①②③④二、填空题
-
11. 写出图中的对顶角:.
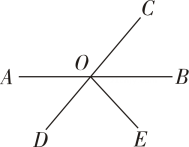 12. “齐天大圣”孙悟空有一个宝贝——金箍棒,当他快速旋转金箍棒时,展现在我们眼前的是一个圆的形象,这说明 .13. 计算: .14. 如图是由射线、、、组成的平面图形,则°.
12. “齐天大圣”孙悟空有一个宝贝——金箍棒,当他快速旋转金箍棒时,展现在我们眼前的是一个圆的形象,这说明 .13. 计算: .14. 如图是由射线、、、组成的平面图形,则°.
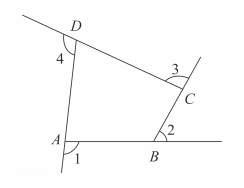 15. 定义:从一个角的顶点引一条射线,把这个角分成两个角,并且这两个角的度数之比为1:2,这条射线叫做这个角的三分线.显然,一个角的三分线有两条.如 , , 是的两条三分线,以点为中心,将按顺时针方向旋转()得到 , 当恰好是的三分线时,的值为 .
15. 定义:从一个角的顶点引一条射线,把这个角分成两个角,并且这两个角的度数之比为1:2,这条射线叫做这个角的三分线.显然,一个角的三分线有两条.如 , , 是的两条三分线,以点为中心,将按顺时针方向旋转()得到 , 当恰好是的三分线时,的值为 . 16. 如图1, 为直线 上一点,作射线 ,使 ,将一个直角三角尺如图摆放,直角顶点在点 处,一条直角边 在射线 上.将图1中的三角尺绕点 以每秒10°的速度按逆时针方向旋转(如图2所示),在旋转一周的过程中,第 秒时, 所在直线恰好平分 ,则 的值为.
16. 如图1, 为直线 上一点,作射线 ,使 ,将一个直角三角尺如图摆放,直角顶点在点 处,一条直角边 在射线 上.将图1中的三角尺绕点 以每秒10°的速度按逆时针方向旋转(如图2所示),在旋转一周的过程中,第 秒时, 所在直线恰好平分 ,则 的值为.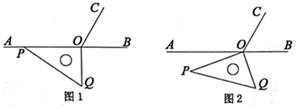
三、解答题
-
17. 如图,在平面内有、、三点,
 (1)、利用尺规,按下面的要求作图要求:不写画法,保留作图痕迹,不必写结论;
(1)、利用尺规,按下面的要求作图要求:不写画法,保留作图痕迹,不必写结论;作射线;
作线段;
连接 , 并在线段上作一条线段 , 使 , 连接 .
(2)、数数看,此时图中线段共有 条18. 如图,∠AOC=30°,∠BOC=80°,OC平分∠AOD.求∠BOD的度数. 19. 某公司员工分别在A,B,C三个住宅区,A区有30人,B区有15人,C区有10人,三个区在一条直线上,位置如下图所示,公司的接送车打算在三个区中选一个作为停靠点,为使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在哪个区?并说明理由.
19. 某公司员工分别在A,B,C三个住宅区,A区有30人,B区有15人,C区有10人,三个区在一条直线上,位置如下图所示,公司的接送车打算在三个区中选一个作为停靠点,为使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在哪个区?并说明理由. 20. 如图,已知直线 , 相交于点O , 是射线, , 比大 , 求的度数.
20. 如图,已知直线 , 相交于点O , 是射线, , 比大 , 求的度数. 21. 如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=60°,将一直角三角板的直角顶点放在点O处,一边ON在射线OB上,另一边OM在直线AB的上方.
21. 如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=60°,将一直角三角板的直角顶点放在点O处,一边ON在射线OB上,另一边OM在直线AB的上方. (1)、在图①中,∠COM=度;(2)、将图①中的三角板绕点O按逆时针方向旋转,使得ON在∠BOC的内部,如图②,若 , 求∠BON的度数;(3)、将图①中的三角板绕点O以每秒15°的速度沿逆时针方向旋转一周,在旋转的过程中,当直线ON恰好平分锐角∠BOC时,旋转的时间是秒.(直接写出结果)22. 将一副直角三角板如图1摆放在直线上(直角三角板和直角三角板 , , , , ),保持三角板不动,将三角板绕点以每秒的速度顺时针旋转直至边第一次重合在直线上,旋转时间记为秒.
(1)、在图①中,∠COM=度;(2)、将图①中的三角板绕点O按逆时针方向旋转,使得ON在∠BOC的内部,如图②,若 , 求∠BON的度数;(3)、将图①中的三角板绕点O以每秒15°的速度沿逆时针方向旋转一周,在旋转的过程中,当直线ON恰好平分锐角∠BOC时,旋转的时间是秒.(直接写出结果)22. 将一副直角三角板如图1摆放在直线上(直角三角板和直角三角板 , , , , ),保持三角板不动,将三角板绕点以每秒的速度顺时针旋转直至边第一次重合在直线上,旋转时间记为秒. (1)、当秒时,平分;(2)、①如图2,旋转三角板 , 使得、同时在直线的异侧,则与数量关系为 ▲ ;
(1)、当秒时,平分;(2)、①如图2,旋转三角板 , 使得、同时在直线的异侧,则与数量关系为 ▲ ;②如图3,继续旋转三角板 , 使得、同时在直线的右侧,猜想与有怎样的数量关系?并说明理由.
(3)、若在三角板开始旋转的同时,另一个三角板也绕点以每秒的速度顺时针旋转,当旋转至直线上时同时停止.请直接写出在旋转过程中,与的数量关系.23. 如图,已知数轴上点表示的数为 , 表示的数为 , 满足.动点从点出发以每秒个单位长度的速度沿数轴向左匀速运动,设运动时间为秒. (1)、写出数轴上点表示的数是 , 点表示的数是;(2)、若点从点出发向左运动,点为的中点,在点到达点之前,求证为定值;(3)、现有动点 , 若点从点以每秒5个单位长度的速度沿数轴向右运动,同时点出发,当点到达原点后立即以每秒2个单位长度的速度沿数轴向左运动,求:当时,则点运动时间的值为.
(1)、写出数轴上点表示的数是 , 点表示的数是;(2)、若点从点出发向左运动,点为的中点,在点到达点之前,求证为定值;(3)、现有动点 , 若点从点以每秒5个单位长度的速度沿数轴向右运动,同时点出发,当点到达原点后立即以每秒2个单位长度的速度沿数轴向左运动,求:当时,则点运动时间的值为.