（第一次学期同步） 6.9直线的相交2023-2024学年浙教版七年级数学

试卷更新日期：2023-12-04 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 在下列图形中，线段PQ的长表示点P到直线MN的距离的是（    ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 下列说法中，正确的是（ ）
    A、相等的角是对顶角 B、若AB=BC，则点B是线段AC的中点 C、在同一平面内，过一点有且仅有一条直线垂直于已知直线 D、一个锐角的补角大于等于该锐角的余角

    查看试题解析

  • 3. 如图，利用工具测量角，则∠1的大小（ ）

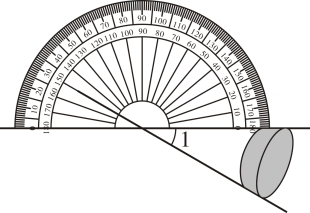    A、30° B、60° C、120° D、150°

    查看试题解析

  • 4. 下列选项中，过点P画AB的垂线CD，三角板放法正确的是（ ）

    A、A B、B C、C D、D

    查看试题解析

  • 5. 下列生活实例中，应用到的数学原理解释错误的一项是（ ）
    A、在两个村庄之间修一条最短的公路，原理是：两点之间线段最短 B、从一条河向一个村庄引一条最短的水渠，原理是：在同一平面内，过一点有且只有一条直线与已知直线垂直 C、把一根木条固定到墙上需要两个钉子，原理是：两点确定一条直线 D、从一个货站向一条高速公路修一条最短的路，原理是：连结直线外一点与已知直线上各点的所有线段中，垂线段最短

    查看试题解析

  • 6. 如图，直线AB，CD相交于点O，∠2=3∠1，∠BOD=108°，则∠1=（ ）

    A、27° B、36° C、81° D、72°

    查看试题解析

  • 7. 如图，直线AB、CD相交于点O，OE⊥CD ， 若∠AOE=50° ， 则∠BOD的度数为（ ）

    A、30° B、40° C、45° D、50°

    查看试题解析

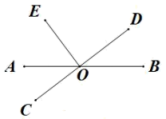  • 8. 如图，经过直线a外一点O的4条直线中，与直线a相交的直线至少有（ ）

    A、1条 B、2条 C、3条 D、4条

    查看试题解析

  • 9. 若四条直线在平面内交点的个数为 a ，则 a 的可能取值有（    ）
    A、3个 B、4个 C、5个 D、6个

    查看试题解析

  • 10. 如图所示，∠BAC=90°，AD⊥BC，则下列结论中，正确的个数为（   ）


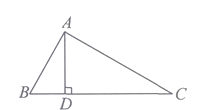
        ①AB⊥AC；  ②AD与AC互相垂直；  ③点C到AB的垂线段是线段AB；

        ④点A到BC的距离是线段AD的长度；  ⑤线段AB的长度是点B到AC的距离；

        ⑥AD+BD>AB．

    A、2个 B、3个 C、4个 D、5个

    查看试题解析

二、填空题

  • 11. 如图，口渴的牛儿在A点处想尽快地到达小河边喝水，它应该沿着线路AB奔跑，其中蕴含的数学依据是.

    查看试题解析

  • 12. 如图，AO⊥BO，O为垂足，直线CD过点O，且∠BOD＝2∠AOC，则∠BOD＝ ．

    查看试题解析

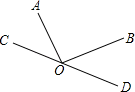  • 13. 如图是一种测量角的仪器，它依据的原理是 ．

    查看试题解析

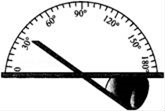  • 14. 如图，直线AB和CD相交于O ， OA平分∠COE ， ∠COE∶∠BOE＝2∶5，则∠EOD的度数为 ．

    查看试题解析

  • 15. 如图，在 4×6 的正方形网格中，点 A、B、C、D、E、F 都在格点上，连接 C、D、E、F 中任意两点得到的所有线段中，与线段 AB 垂直的线段是.

    查看试题解析

  • 16. 如图，在平面内，两条直线l1 ， l2相交于点O，对于平面内任意一点M，若p，q分别是点M到直线l1 ， l2 ， 的距离，则称（p，q）为点M的“距离坐标”．根据上述规定，“距离坐标”是（3，2）的点共有个．

    查看试题解析

三、解答题

  • 17. 如图，直线AB，CD相交于点O，OE平分∠BOC，OF⊥OE，且∠AOD=66°．求∠BOF的度数．

    查看试题解析

  • 18. 如图，AO⊥BO，CO⊥DO，O是垂足，∠BOC=50°．求∠AOD的度数．

    查看试题解析

  • 19. 如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，且∠BON=55°，求∠BOD的度数.

    查看试题解析

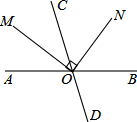  • 20. 如图所示，A、B、C、D、E五个城市，它们之间原有道路相通，现在打算在C、E两城市之间沿直线再修建一条公路，这条公路与原公路的交叉处必须设立交桥，问怎样确定立交桥的位置？应架设几座立交桥？

    查看试题解析

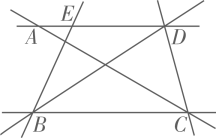  • 21. 平面内有任意一点P和∠1，按要求解答下列问题：

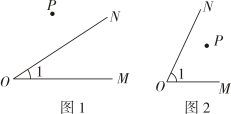    (1)、当点P在∠1外部时，如图1，过点P作PA⊥OM，PB_⊥ON，垂足分别为A，B，量一量∠APB和∠1的度数，用数学式子表达它们之间的数量关系．
    (2)、当点P在∠1内部时，如图2，以点P为顶点作∠APB，使∠APB的两边分别和∠1的两边垂直，垂足分别为A，B，量一量∠APB和∠1的度数，用数学式子表达∠APB和∠1的数量关系．
    (3)、由上述情形，用文字语言叙述结论：如果一个角的两边分别和另一个角的两边垂直，那么这两个角
    (4)、若∠1=50°，∠P的两边和∠1的两边垂直，则∠P的度数为

    查看试题解析

  • 22. 如图（1），点 O 为直线 AB 上一点，过点 O 作射线 OC ，将一直角的直角顶点放在点 O 处，即 ∠MON ， 反向延长射线 ON ，得到射线 OD .

    (1)、当 ∠MON 的位置如图（1）所示时，使 ∠NOB=20∘ ，若 ∠BOC=120∘ ，求 ∠COD 的度数.
    (2)、当 ∠MON 的位置如图（2）所示时，使一边 OM 在 ∠BOC 的内部，且恰好平分 ∠BOC ，

    问：射线 ON 的反向延长线 OD 是否平分 ∠AOC? 请说明理由：注意：不能用问题（1）中的条件

    (3)、当 ∠MON 的位置如图 (3) 所示时，射线 ON 在 ∠AOC 的内部，若 ∠BOC=120∘ .试探究 ∠AOM 与 ∠NOC 之间的数量关系，不需要证明，写出结论.

    查看试题解析

  • 23. 已知∠AOB=160°，∠COE是直角，OF平分∠AOE.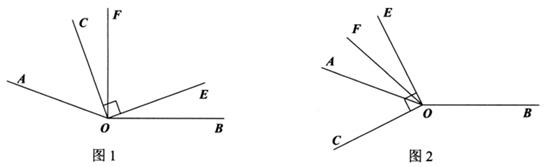

    (1)、如图1，若∠COF=32°，则∠BOE=；
    (2)、如图1，若∠COF=m°，则∠BOE=；∠BOE与∠COF的数量关系为.
    (3)、在已知条件不变的前提下，当∠COE绕点О逆时针转动到如图2的位置时，第（2）问中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.

    查看试题解析