2024高考一轮复习第三十二讲数列综合

试卷更新日期：2023-12-04 类型：一轮复习

进入出卷网下载

一、选择题

1. 南宋数学家杨辉在《详解九章算法》中，研究了二阶等差数列．若 ${a_{n + 1} - a_{n}}$ 是公差不为零的等差数列，则称数列 ${a_{n}}$ 为二阶等差数列．现有一个“三角垛”，共有40层，各层小球个数构成一个二阶等差数列，第一层放1个小球，第二层放3个小球，第三层放6个小球，第四层放10个小球， $⋯$ ，则第40层放小球的个数为（）

A、1640 B、1560 C、820 D、780

查看试题解析
2. 斐波那契数列 ${a_{n}}$ 满足 $a_{1} = a_{2} = 1 ， a_{n} = a_{n - 1} + a_{n - 2} (n \geq 3)$ ，其每一项称为“斐波那契数”.如图，在以斐波那契数为边长的正方形拼成的长方形中，利用下列各图中的面积关系，推出 $\frac{a_{1}^{2} + a_{2}^{2} + ⋯ + a_{2023}^{2}}{a_{2023}}$ 是斐波那契数列的第（）项.

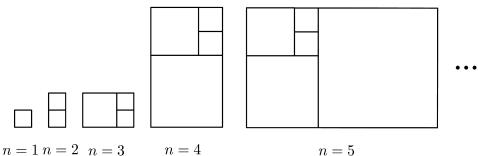A、2022 B、2023 C、2024 D、2025

查看试题解析
3. 等比数列 ${a_{n}}$ 满足 $a_{2} + 8 a_{5} = 0$ ，设数列 ${\frac{1}{a_{n}}}$ 的前 $n$ 项和为 $S_{n}$ ，则 $\frac{S_{5}}{S_{2}}$ =（）

A、-11 B、-8 C、5 D、11

查看试题解析
4. 定义 $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ ，已知数列 ${a_{n}}$ 为等比数列，且 $a_{3} = 1$ ， $| \begin{array}{l} a_{6} & 8 \\ 8 & a_{8} \end{array} | = 0$ ，则 $a_{7} =$ （）

A、4 B、±4 C、8 D、±8

查看试题解析
5. 在数列 ${b_{n}}$ 中，若有 $b_{m} = b_{n}$ （ $m$ ， $n$ 均为正整数，且 $m \neq n$ ），就有 $b_{m + 1} = b_{n + 1}$ ，则称数列 ${b_{n}}$ 为“递等数列”.已知数列 ${a_{n}}$ 满足 $a_{5} = 5$ ，且 $a_{n} = n (a_{n + 1} - a_{n})$ ，将“递等数列” ${b_{n}}$ 前 $n$ 项和记为 $S_{n}$ ，若 $b_{1} = a_{1} = b_{4}$ ， $b_{2} = a_{2}$ ， $S_{5} = a_{10}$ ，则 $S_{2023} =$ （）

A、4720 B、4719 C、4718 D、4716

查看试题解析
6. 数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{1} = \frac{1}{2}$ ，若该数列满足 $a_{n} + 2 S_{n} S_{n - 1} = 0 (n \geq 2)$ ，则下列命题中错误的是（）

A、 ${\frac{1}{S_{n}}}$ 是等差数列 B、 $S_{n} = \frac{1}{2 n}$ C、 $a_{n} = - \frac{1}{2 n (n - 1)}$ D、 ${S_{2^{n}}}$ 是等比数列

查看试题解析
7. 设 $S_{n}$ 是一个无穷数列 ${a_{n}}$ 的前 $n$ 项和，若一个数列满足对任意的正整数 $n$ ，不等式 $\frac{S_{n}}{n} < \frac{S_{n + 1}}{n + 1}$ 恒成立，则称数列 ${a_{n}}$ 为和谐数列，有下列3个命题：
①若对任意的正整数 $n$ 均有 $a_{n} < a_{n + 1}$ ，则 ${a_{n}}$ 为和谐数列；
②若等差数列 ${a_{n}}$ 是和谐数列，则 $S_{n}$ 一定存在最小值；
③若 ${a_{n}}$ 的首项小于零，则一定存在公比为负数的一个等比数列是和谐数列．
以上3个命题中真命题的个数有（）个

A、0 B、1 C、2 D、3

查看试题解析
8. 已知等比数列 ${a_{n}}$ 的前n项和与前n项积分别为 $S_{n}$ ， $T_{n}$ ，公比为正数，且 $a_{3} = 16$ ， $S_{3} = 112$ ，则使 $T_{n} > 1$ 成立的n的最大值为（）

A、8 B、9 C、12 D、13

查看试题解析
9. 由中国古代劳动人民发明于东周春秋时期，距今已2000多年.龙被视为中华古老文明的象征，大型龙类风筝放飞场面壮观，气势磅磗，因而广受喜爱.某团队耗时4个多月做出一长达200米、重约25公斤，“龙身”共有180节“鱗片”的巨龙风筝.制作过程中，风箏骨架可采用竹子制作，但竹子易断，还有一种耐用的碳杆材质也可做骨架，但它比竹质的成本高.最终团队决定骨架材质按图中规律排列（即相邻两碳质骨架之间的竹质骨架个数成等差数列），则该“龙身”中竹质骨架个数为（）

A、161 B、162 C、163 D、164

查看试题解析
10. 如图的形状出现在南宋数学家杨辉所著的《详解九章算法·商功》中，后人称为“三角垛”.“三角垛”的最上层有1个球，第二层有3个球，第三层有6个球……在2015年世乒赛期间，苏州某景点就用乒乓球堆成“三角垛”型的装饰品，假设一个“三角垛”装饰品共有n层，记使用的乒乓球数量为 $f (n)$ ，则 $f (n) =$ （）
（参考公式： $1^{2} + 2^{2} + 3^{2} + ⋯ + n^{2} = \frac{1}{6} n (n + 1) (2 n + 1)$ ）

A、 $\frac{1}{6} n (n + 1) (2 n + 1)$ B、 $\frac{n (n + 1)}{2}$ C、 $\frac{1}{3} n (n + 1) (n + 2)$ D、 $\frac{1}{6} n (n + 1) (n + 2)$

查看试题解析

二、填空题

11. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且点 $(a_{n} ， S_{n})$ 总在直线 $y = 2 x - 1$ 上，则数列 ${n \cdot a_{n}}$ 的前 $n$ 项和 $T_{n} =$ .

查看试题解析
12. 参考《九章算术》中“竹九节”问题，提出：一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共2升，下面3节的容积共3升，则第5节的容积为升．

查看试题解析
13. 如图给出的三角形数阵，图中虚线上的数 $1$ 、 $3$ 、 $6$ 、 $10$ 、 $⋯$ ，依次构成数列 ${a_{n}}$ ，则 $\frac{1}{a_{1}} + \frac{1}{a_{2}} + ⋯ + \frac{1}{a_{10}} =$ .

查看试题解析
14. $S_{n}$ 是数列 ${a_{n}}$ 前 $n$ 项和， $a_{1} = 3$ ， $a_{n + 1} = a_{n} - \frac{4}{4 n^{2} - 1}$ ，给出以下四个结论：
① $a_{n} = \frac{2 n + 1}{2 n - 1}$ ；
② $a_{1} + a_{1} a_{2} + ⋯ + a_{1} a_{2} ⋯ a_{n} = n^{2} + 2 n$ ；
③ $S_{n} > n + l n (2 n + 1)$ ；
④ $S_{n} > n^{2} + l n (2 n^{2} + 1)$ .
其中正确的是（写出全部正确结论的番号）.

查看试题解析

三、解答题

15. 数列 ${a_{n}}$ 中， $a_{1} = 2$ ， $a_{n + 1} = 2 a_{n} - 1$ .

(1)、求数列 ${a_{n}}$ 的通项公式 $a_{n}$ ；

(2)、若 $b_{n} = a_{n} + n$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
16. 已知等差数列 ${a_{n}}$ 满足 $a_{2} = 4$ ， $2 a_{4} - a_{5} = 7$ ，公比不为 $- 1$ 的等比数列 ${b_{n}}$ 满足 $b_{3} = 4$ ， $b_{4} + b_{5} = 8 (b_{1} + b_{2})$ .

(1)、求 ${a_{n}}$ 与 ${b_{n}}$ 通项公式；

(2)、设 $c_{n} = \frac{3}{a_{n} a_{n + 1}} + b_{n}$ ，求 ${c_{n}}$ 的前n项和 $S_{n}$ .

查看试题解析
17. 已知等差数列 ${a_{n}}$ 满足 $a_{1} = 1$ ， $a_{2} + a_{5} = 2 (a_{3} + 1)$ ．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、设 ${a_{n}}$ 的前n项和为 $S_{n}$ ，求数列 ${\frac{1}{n + S_{n}}}$ 的前n项和 $T_{n}$ ．

查看试题解析
18. 已知数列 ${a_{n}}$ 满足 $a_{1} = 1$ ， $a_{2} = 2$ ，且数列 ${a_{n + 1} - a_{n}}$ 是公比为2的等比数列．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、令 $b_{n} = \frac{2 n + 1}{3^{n}} \cdot a_{n}$ ，数列 ${b_{n}}$ 是否有最大项？若有，求出最大项；若没有，说明理由．

查看试题解析
19. 已知数列 ${a_{n}}$ 满足 $a_{1} = 1$ ， $a_{2 n + 1} = a_{2 n} + 1$ ， $a_{2 n} = 2 a_{2 n - 1}$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、设 $T_{n} = \frac{1}{a_{1}} + \frac{1}{a_{2}} + ⋯ + \frac{1}{a_{n}}$ ，求证： $T_{2 n} < 3$ .

查看试题解析
20. 已知数列 ${a_{n}}$ 是首项为1的等差数列，公差 $d > 0$ ，设数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $S_{1}$ ， $S_{2}$ ， $S_{4}$ 成等比数列．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、求数列 ${| a_{n} - 8 |}$ 的前 $n$ 项和 $T_{n}$ ．

查看试题解析
21. 已知 $S_{n}$ 是数列 ${a_{n}}$ 的前n项和，且 $S_{n} = 2^{n + 1} - 1 (n \in N^{*})$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $b_{n} = \frac{2^{n + 1}}{(a_{n} - 1) (a_{n + 1} - 1)}$ ， $T_{n}$ 是 ${b_{n}}$ 的前 $n$ 项和，证明： $T_{n} < \frac{4}{3}$ ．

查看试题解析
22. 已知 $a_{1} = 1 ， {a_{n} + 1}$ 是公比为2的等比数列， ${b_{n}}$ 为正项数列， $b_{1} = 1$ ，当 $n \geq 2$ 时， $(2 n - 3) b_{n} = (2 n - 1) b_{n - 1}$ ．

(1)、求数列 ${a_{n}} ， {b_{n}}$ 的通项公式；

(2)、记 $c_{n} = a_{n} \cdot b_{n}$ ．求数列 ${c_{n}}$ 的前n项和 $T_{n}$ ．

查看试题解析

2024高考一轮复习 第三十二讲 数列综合

一、选择题

二、填空题

三、解答题

2024高考一轮复习第三十二讲数列综合