2024高考一轮复习第三十一讲等比数列及其前n项和

试卷更新日期：2023-12-04 类型：一轮复习

进入出卷网下载

一、选择题

1. 在等比数列 ${a_{n}}$ 中， $a_{4}$ 和 $a_{12}$ 是方程 $x^{2} + 3 x + 1 = 0$ 的两根，则 $a_{8} =$ （）

A、3 B、5 C、-1 D、 $\pm 1$

查看试题解析
2. 已知等比数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ， $a_{4} = 1$ ， $S_{8} = 3 (a_{2} + a_{4} + a_{6} + a_{8})$ ，则（）

A、 $a_{n} = 2^{n - 4}$ B、 $a_{n} = 2^{n + 4}$ C、 $S_{n} = 16 + 2^{4 - n}$ D、 $S_{n} = 16 - 2^{4 - n}$

查看试题解析
3. 已知等比数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，若 $\frac{S_{3}}{S_{6}} = \frac{1}{6}$ ，则 $\frac{S_{9}}{S_{3}} =$ （）

A、12 B、36 C、31 D、33

查看试题解析
4. 已知 ${a_{n}}$ 是公差不为0的等差数列， $a_{1} = 2$ ，若 $a_{1} ， a_{3} ， a_{7}$ 成等比数列，则 $a_{2023} =$ （）

A、2023 B、2024 C、4046 D、4048

查看试题解析
5. 现有17匹善于奔驰的马，它们从同一个起点出发，测试它们一日可行的路程．已知第i（ $i = 1 ， 2 ， \dots ， 16$ ）匹马的日行路程是第 $i + 1$ 匹马日行路程的1.05倍，且第16匹马的日行路程为315里，则这17匹马的日行路程之和约为（取 $1.0 5^{17} = 2.292$ ）（）

A、7750里 B、7752里 C、7754里 D、7756里

查看试题解析
6. 已知等比数列 ${a_{n}}$ 的公比为 $q$ （ $q > 0$ 且 $q \neq 1$ ），若 $a_{6} + 8 a_{1} = a_{4} + 8 a_{3}$ ，则 $q$ 的值为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、2 D、4

查看试题解析
7. 记公差不为0的等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ .若 $a_{2} ， a_{5} ， a_{10}$ 成等比数列， $S_{10} = 160$ ，则 $a_{6} =$ （）

A、17 B、19 C、21 D、23

查看试题解析
8. 已知等比数列 ${a_{n}}$ 中， $4 a_{1}$ ， $\frac{1}{2} a_{3}$ ， $3 a_{2}$ 成等差数列，则 $\frac{a_{2021} - a_{2022}}{a_{2022} - a_{2023}} =$ （）

A、 $\frac{1}{4}$ 或 $- 1$ B、4 C、-1 D、 $\frac{1}{4}$

查看试题解析
9. 在递增等比数列 ${a_{n}}$ 中， $a_{3} = 4$ ，且 $3 a_{5}$ 是 $a_{6}$ 和 $a_{7}$ 的等差中项，则 $a_{10} =$ （）

A、256 B、512 C、1024 D、2048

查看试题解析
10. 已知等比数列 ${a_{n}}$ 的公比为负数，且 $a_{3} · a_{9} = 2 a_{5}^{2}$ ，已知 $a_{2} = 1$ ，则 $a_{1} =$ (　　)

A、 $\frac{1}{2}$ B、 $- \frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、2

查看试题解析
11. 已知数列 ${a_{n}}$ 为递减的等比数列， $n \in N^{*}$ ，且 $a_{2} a_{7} = 32$ ， $a_{3} + a_{6} = 18$ ，则 ${a_{n}}$ 的公比为（）

A、 $\frac{1}{2}$ B、 ${(\frac{1}{2})}^{\frac{3}{5}}$ C、 $2^{\frac{3}{5}}$ D、 $2$

查看试题解析
12. 2020年12月17日凌晨1时59分，嫦娥五号返回器携带月球样品成功着陆，这是我国首次实现了地外天体采样返回，标志着中国航天向前又迈出了一大步．月球距离地球约38万千米，有人说：在理想状态下，若将一张厚度约为0.1毫米的纸对折 $n$ 次其厚度就可以超过到达月球的距离，那么至少对折的次数 $n$ 是（）（ $l g 2 \approx 0.3$ ， $l g 3.8 \approx 0.6$ ）

A、40 B、41 C、42 D、43

查看试题解析
13. 已知等比数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，若 $\frac{S_{5}}{S_{10}} = \frac{1}{33} ， a_{4} = 8$ ，则 $S_{8} =$ （）

A、127 B、254 C、510 D、255

查看试题解析
14. 《莱茵德纸草书》（RhindPapyrus）是世界上最古老的数学著作之一，书中有这样一道题目：把 $93$ 个面包分给 $5$ 个人，使每个人所得面包个数成等比数列，且使较小的两份面包个数之和等于中间一份面包个数的四分之三，则中间一份面包的个数为（）

A、8 B、12 C、16 D、20

查看试题解析

二、填空题

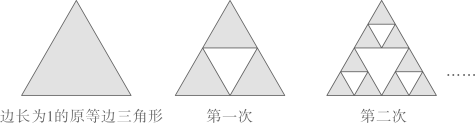
15. 已知公比大于 $1$ 的等比数列 ${a_{n}}$ 满足 $a_{2} + a_{3} = 12$ ， $a_{4} = 16$ ，则 ${a_{n}}$ 的公比 $q =$ ．

查看试题解析
16. 已知{ $a_{n}$ }是公比为q的等比数列，且 $a_{2}$ 、 $a_{4}$ 、 $a_{6}$ 成等差数列，则 $q^{2}$ =.

查看试题解析
17. 已知 $S_{n}$ 是等比数列 ${a_{n}}$ 的前 $n$ 项和， $a_{3} = 1$ ， $2 S_{3} = 7 a_{2}$ ，则 $S_{5} =$ ．

查看试题解析
18. 如图，将一个边长为1的正三角形分成四个全等的正三角形，第一次挖去中间的一个小三角形，将剩下的三个小正三角形，再分别从中间挖去一个小三角形，保留它们的边，重复操作以上做法，得到的集合为谢尔宾斯基三角形.设 $A_{n}$ 是第 $n$ 次挖去的小三角形面积之和（如 $A_{1}$ 是第1次挖去的中间小三角形面积， $A_{2}$ 是第2次挖去的三个小三角形面积之和），则 $A_{n} =$ ；若操作 $n$ 次后剩余部分面积不大于原图面积的一半，则 $n$ 的最小值为.

查看试题解析

三、解答题

19. 已知数列 ${a_{n}}$ 满足 $a_{1} = 3$ ， $n a_{n + 1} = 3 (n + 1) a_{n}$ ．

(1)、证明： ${\frac{a_{n}}{n}}$ 是等比数列．

(2)、设 $b_{n} = \frac{n^{2}}{a_{n}}$ ，求数列 ${b_{n}}$ 的前n项和 $T_{n}$ ．

查看试题解析
20. 设数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，已知 $a_{1} = 1$ ，且数列 ${3 - \frac{2 S_{n}}{a_{n}}}$ 是公比为 $\frac{1}{3}$ 的等比数列.

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $b_{n} = (2 n + 1) 3^{n - 1}$ ，求其前 $n$ 项和 $T_{n}$

查看试题解析
21. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $S_{1} = 2$ ， $S_{n} = \frac{n}{n + 2} a_{n + 1}$ ， $b_{n} = \frac{S_{n}}{n}$ $(n \in N^{*})$ ．

(1)、求数列 ${b_{n}}$ 的通项公式；

(2)、设 $c_{n} = \frac{b_{n}}{(b_{n} - 1) (b_{n + 1} - 1)}$ ，数列 ${c_{n}}$ 的前 $n$ 项和 $T_{n}$ ，求证： $\frac{2}{3} \leq T_{n} < 1$ ．

查看试题解析
22. 已知数列 ${a_{n}}$ ， ${b_{n}}$ 的前n项和分别为 $S_{n}$ ， $T_{n}$ ，且 $b_{1} = \frac{1}{2}$ ， $S_{n} = \frac{1}{2} n^{2} + \frac{1}{2} n$ ，当 $n > 1$ 时，满足 $2 b_{n} a_{n - 1} = b_{n - 1} a_{n}$ ．

(1)、求 $a_{n}$ ；

(2)、求 $T_{n}$ ．

查看试题解析

2024高考一轮复习 第三十一讲 等比数列及其前n项和

一、选择题

二、填空题

三、解答题

2024高考一轮复习第三十一讲等比数列及其前n项和