(第一次学期同步) 6.5角与角的度量—2023-2024学年浙教版七年级数学
试卷更新日期:2023-12-04 类型:同步测试
一、选择题
-
1. 下面四幅图中的∠AOB不等于的是( )A、
 B、
B、 C、
C、 D、
D、 2. 把化为用度表示,下列正确的是( )A、 B、 C、 D、3. 下列四个图中,能用 , , 三种方法表示同一个角的是( )A、
2. 把化为用度表示,下列正确的是( )A、 B、 C、 D、3. 下列四个图中,能用 , , 三种方法表示同一个角的是( )A、 B、
B、 C、
C、 D、
D、 4. 已知 , 下面结论正确的是( )A、 B、 C、 D、5. 如图,下列说法错误的是( )
4. 已知 , 下面结论正确的是( )A、 B、 C、 D、5. 如图,下列说法错误的是( ) A、 是一个平角 B、 也可以表示为 C、 也可以表示为 D、 也可以表示为6. 下列四个图形中,能用 、 、 三种方法表示同一角的图形是( )A、
A、 是一个平角 B、 也可以表示为 C、 也可以表示为 D、 也可以表示为6. 下列四个图形中,能用 、 、 三种方法表示同一角的图形是( )A、 B、
B、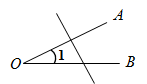 C、
C、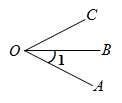 D、
D、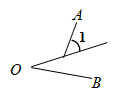 7. 如图所示下列说法正确的是( )
7. 如图所示下列说法正确的是( ) A、 就是 B、 可以用 表示 C、 和 是同一个角 D、 和 不是同一个角8. 如图,是直线,是直线上一点,、是两条射线,则图中小于平角的角有( )
A、 就是 B、 可以用 表示 C、 和 是同一个角 D、 和 不是同一个角8. 如图,是直线,是直线上一点,、是两条射线,则图中小于平角的角有( ) A、3个 B、4个 C、5个 D、6个9. 下列说法 中,不正确的是( )A、∠AOB的顶点是O点 B、射线BO,射线AO分别是∠AOB的两条边 C、∠AOB的边是两条射线 D、∠AOB 与∠BOA表示同一个角10. 如图所示,下列表示角的方法中,错误的是( )
A、3个 B、4个 C、5个 D、6个9. 下列说法 中,不正确的是( )A、∠AOB的顶点是O点 B、射线BO,射线AO分别是∠AOB的两条边 C、∠AOB的边是两条射线 D、∠AOB 与∠BOA表示同一个角10. 如图所示,下列表示角的方法中,错误的是( ) A、 与 表示同一个角 B、 也可用 表示 C、图中共有三个角,分别是 D、 表示
A、 与 表示同一个角 B、 也可用 表示 C、图中共有三个角,分别是 D、 表示二、填空题
-
11. 已知 , 比较这两个角的大小, 结果为∠1∠2.12. 计算:.13. 用放大倍数为4倍的放大镜看一个10°的角,则观察到的角的度数是.14. 如图,在平面内有A,B,C三点.请画直线AC,线段BC,射线AB,数数看,此时图中共有个钝角.
 15. 在∠AOB中,C,D分别为边OA,OB上的点(不与顶点O重合).对于任意锐角∠AOB,下面三个结论中,①作边OB的平行线与边OA相交,这样的平行线能作出无数条;②连接CD,存在∠ODC是直角;③点C到边OB的距离不超过线段CD的长.所有正确结论的序号是.16. 将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3,这三个圆心角中最大的圆心角度数为
15. 在∠AOB中,C,D分别为边OA,OB上的点(不与顶点O重合).对于任意锐角∠AOB,下面三个结论中,①作边OB的平行线与边OA相交,这样的平行线能作出无数条;②连接CD,存在∠ODC是直角;③点C到边OB的距离不超过线段CD的长.所有正确结论的序号是.16. 将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3,这三个圆心角中最大的圆心角度数为三、解答题
-
17. 读句画图填空:(1)、画∠AOB;(2)、作射线OC,使∠AOC= ∠AOB;(3)、由图可知,∠BOC=∠AOB.18. 如图所示,写出:
 (1)、能用一个字母表示的角.(2)、以为顶点的角.(3)、图中共有几个小于平角的角?19. 计算:(1)、﹣12021﹣[(﹣2)2÷×6+4];(2)、132°25′﹣55°43′20″.20. 图中共有几个角?用适当的方式表示这些角.
(1)、能用一个字母表示的角.(2)、以为顶点的角.(3)、图中共有几个小于平角的角?19. 计算:(1)、﹣12021﹣[(﹣2)2÷×6+4];(2)、132°25′﹣55°43′20″.20. 图中共有几个角?用适当的方式表示这些角. 21.
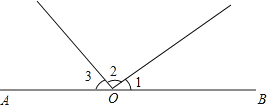
21.如图,AB是一条直线,如果∠1=65°15′,∠2=78°30′,求∠3的度数.
 22. 如图,已知线段AB和CD,利用直尺,圆规和量角器按要求完成下列问题:
22. 如图,已知线段AB和CD,利用直尺,圆规和量角器按要求完成下列问题: (1)、①作线段AE,使点B为线段AE的中点;
(1)、①作线段AE,使点B为线段AE的中点;②画射线EA与直线CD相交于F点;
(2)、用量角器度量得∠AFC的大小为°(精确到度).要求:不写画法,保留作图痕迹.
23. (1)在∠AOB内部画1条射线OC,则图1中有 个不同的角;(2)在∠AOB内部画2条射线OC,OD,则图2中有 个不同的角;
(3)在∠AOB内部画3条射线OC,OD,OE,则图3中有 个不同的角;
(4)在∠AOB内部画10条射线OC,OD,OE…,则图中有 个不同的角;
(5)在∠AOB内部画n条射线OC,OD,OE…,则图中有 个不同的角.
 24. 请用下列工具按要求画图,并标出相应的字母.
24. 请用下列工具按要求画图,并标出相应的字母.已知:点P在直线a上,点Q在直线a外.
( 1 )画线段;
( 2 )画线段的中点M;
( 3 )画直线b,使于点M;
( 4 )直线b与直线a交于点N;
( 5 )利用半圆仪测量出(精确到).
