（第一次学期同步） 6.4线段的和差—2023-2024学年浙教版七年级数学

试卷更新日期：2023-12-04 类型：同步测试

进入出卷网下载

一、选择题

1. 若C是线段AB的中点，AB=6 cm，则BC=（）

A、3cm B、4.5cm C、6cm D、12cm

查看试题解析
2. 如图，C是线段AB的中点，D是线段AC的中点，若AB=8，则CD的长为（）

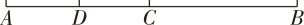A、2 B、4 C、6 D、8

查看试题解析
3. 如图，点B，点C都在线段AD上，若AD＝2BC，则（）

A、AB＝CD B、AB+CD＝BC C、AC-CD＝BC D、AD+BC＝2AC

查看试题解析
4. 如图，观察图形，下列结论中不正确的是（）

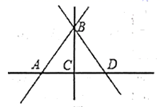A、图中有 $5$ 条线段 B、直线 $B A$ 和直线 $A B$ 是同一条直线 C、 $A B + B D > A D$ D、射线 $A C$ 和射线 $A D$ 是同一条射线

查看试题解析
5. 下列说法正确的是（）

A、一点确定一条直线 B、射线比直线短 C、两点之间，线段最短 D、若AB=BC，则B为AC的中点

查看试题解析
6. 如图，点M是AB的中点，点N是BD的中点， $A B = 8 c m ， B C = 12 c m ， C D = 6 c m$ ．则MN的长为（）

A、7cm B、10cm C、13cm D、16cm

查看试题解析
7. 点A，B，P在同一直线上，下列说法正确的是（）

A、若AB＝2PA，则P是AB的中点 B、若AB＝PB，则P是AB的中点 C、若AB＝2PB，则P是AB的中点 D、若AB＝2PA＝2PB，则P是AB的中点

查看试题解析
8. 点A、B、C是同一直线上的三个点，若，，则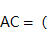

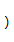A、11cm B、5cm C、11cm或5cm D、11cm或3cm

查看试题解析
9. 如图，下列关系式中与图不符合的是（）

A、 $A C + C D = A B - B D$ B、 $A B - C B = A D - B C$ C、 $A B - C D = A C + B D$ D、 $A D - A C = C B - D B$

查看试题解析
10. 如图，A、O、B两点在数轴上对应的数分别为﹣20、0、40，C点在A、B之间，在A、B两点处各放一个挡板，M、N两个小球同时从C处出发，M以2个单位/秒的速度向数轴负方向运动，N以4个单位/秒的速度向数轴正方向运动，碰到挡板后则反方向运动，速度大小不变．设两个小球运动的时间为t秒钟（0＜t＜40），当M小球第一次碰到A挡板时，N小球刚好第一次碰到B挡板．则：①C点在数轴上对应的数为0；②当10＜t＜25时，N在数轴上对应的数可以表示为80﹣4t；③当25＜t＜40时，2MA+NB始终为定值160；④只存在唯一的t值，使3MO＝NO，以上结论正确的有（　　）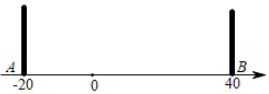

A、①②③④ B、①③ C、②③ D、①②④

查看试题解析

二、填空题

11. 如图，点C，M，N在线段AB上， $A C = 12 ， B C = 6 ， A M = \frac{1}{3} A C ， B N = \frac{1}{3} B C$ .则线段MN的长为.

查看试题解析
12. 如图，在直线 $m$ 上顺次取 $A$ ， $B$ ， $C$ 三点，使得 $A B = 3 c m$ ， $B C = 1 c m$ ，取线段 $A C$ 的中点 $D$ ，若动点 $P$ 从点 $A$ 出发以 $2 c m / s$ 的速度沿射线 $A C$ 方向运动，设运动时间为 $t s$ ，当 $D P = 5 D B$ 时， $t$ 的值为 $s$ ．

查看试题解析
13. 点P为线段AB的三等份点，Q为线段AB上一点，且AQ=2，AB=9，则PQ=

查看试题解析
14. 直线AB上有两点C、D ，点C在A、B之间，满足 $C A = \frac{1}{3} C B ， C D = \frac{1}{3} C A$ ，若AB＝20，则BD＝．

查看试题解析
15. 如图，点 $C$ 是线段 $A B$ 上一点， $A C > B C$ ，点 $M$ 是线段 $A B$ 的中点，点 $N$ 是线段 $B C$ 的中点， $A M = 8$ ， $C N = 3$ ，则线段 $M N$ 的长度为.

查看试题解析
16. 如图所示：已知 $A B = 5 cm$ ， $B C = 10 cm$ ，现有 $P$ 点和 $Q$ 点分别从 $A$ ， $B$ 两点出发相向运动， $P$ 点速度为 $2 cm/s$ ， $Q$ 点速度为 $3 cm/s$ ，当 $Q$ 到达 $A$ 点后掉头向 $C$ 点运动， $Q$ 点在向 $C$ 的运动过程中经过 $B$ 点时，速度变为 $4 cm/s$ ， $P$ ， $Q$ 两点中有一点到达 $C$ 点时，全部停止运动，那么经过 $s$ 后 $P Q$ 的距离为 $0.5 cm$ ．

查看试题解析

三、解答题

17. 如图，C，D，E是线段 $A B$ 上的点， $A C = 5$ ， $D B = 3$ ，点C，E分别是线段 $A D$ ， $B D$ 的中点，求 $C E$ 的长．

查看试题解析
18. 如图， $A B = 12 cm$ ，点C是线段 $A B$ 的中点，D、E分别是线段 $A C$ 、 $C B$ 上的点， $A D = \frac{1}{3} A C$ ， $D E = 8 cm$ ，求线段 $C E$ 的长.

查看试题解析
19. 如图，线段AB=2cm．按要求画出图形，并解答下面的问题：延长线段AB至点C，使BC=2AB，取线段AC的中点G．求线段BG的长．

查看试题解析
20. 如图，在数轴上有A，B两点，其中点A在点B的左侧，已知点B对应的数为4，点A对应的数为a.

(1)、若a＝ $\frac{7}{6} \times (\frac{1}{6} - \frac{1}{3}) \times \frac{3}{14} \div \frac{3}{5}$ ×72，则线段AB的长为（直接写出结果）.

(2)、若点C在射线AB上（不与A，B重合），且2AC-3BC＝6，求点C对应的数（结果用含a的式子表示）.

(3)、若点M在线段AB之间，点N在点A的左侧（M、N均不与A、B重合），且AM-BM＝2.当 $\frac{A M}{A N}$ ＝3，BN＝6BM时.求a的值.

查看试题解析
21. 补全解题过程：
已知：如图，点 $C$ 在线段 $A B$ 上，且 $A C = 6 c m$ ，点 $E$ 和点 $F$ 分别是线段 $A B$ 、 $A C$ 的中点， $E F = 5 c m$ ．
求线段 $A B$ 的长．
解： $∵$ 点 $F$ 是线段 $A C$ 的中点， $A C = 6 c m$ ，
$∴ C F =$   ▲   $=$   ▲   $c m$ ．
$∵ E F = 5 c m$ ，
$∴ C E = E F - C F = 2 c m$ ．
$∴ A E =$   ▲   $+ C E =$   ▲   $c m$ ．
$∵$ 点 $E$ 是线段 $A B$ 的中点，
$∴ A B = 2 A E =$   ▲   $c m$ ．

查看试题解析
22. 已知A，B两地相距a千米，C地在AB的延长线上，且BC= $\frac{a}{3}$ 千米，D是A，C两地的中点．

(1)、求AD的长(结果用含a的代数式表示)．

(2)、若BD=90千米，求a的值．

(3)、甲、乙两车分别从A，D两地同时出发，都沿着直线AC匀速去C地，经4小时甲追上乙．当甲追上乙后甲马上原路返回，甲返回行驶1小时时发现甲车距D地50千米．已知a=600千米，求乙车行驶的平均速度．

查看试题解析
23. 阅读理解：
【探究与发现】在一次数学探究活动中，数学兴趣小组发现可以通过“两数的差”来表示“数轴上两点间的距离”，如图①中三条线段的长度可表示为： $A B = 4 - 2 = 2$ ， $C B = 4 - (- 2) = 6$ ， $D C = - 2 - (- 4) = 2$ ， …结论：数轴上任意两点表示的数分别为a，b（ $b > a$ ），则这两个点间的距离为 $b - a$ （即：用较大的数减去较小的数）．
【理解与应用】

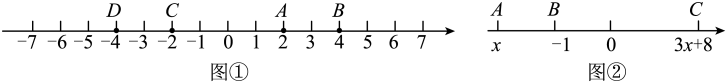(1)、在数轴上分别有点M、N、H，其中M、N表示的数分别为 $- 20$ ， 2020，点H为线段MN的中点，若点H表示的数为m，求m的值；

(2)、如图②，数轴上点A，B，C表示的数分别为x， $- 1$ ， $3 x + 8$ ，且 $A B = \frac{1}{3} B C$ ，求A，C分别表示什么数？

(3)、在（2）的条件下，图②的数轴上是否存在点D，使 $D A + D C = 3 D B$ ？若存在，请直接写出点D表示的数，若不存在，请说明理由．（点D不与点A、B、C重合）．

查看试题解析