(第一次学期同步) 6.3线段的长短比较—2023-2024学年浙教版七年级数学
试卷更新日期:2023-12-04 类型:同步测试
一、选择题
-
1. 把弯曲的道路改直就能缩短路程,下列数学语言解释正确的是( )A、垂线段最短 B、两点确定一条直线 C、两点之间线段最短 D、对顶角相等2. 如图,我们可借助圆规判断线段AB和CD的长短,由图可知( )
 A、AB>CD B、AB=CD C、AB<CD D、无法确定3. 如图,小红将三角形纸片沿虚线剪去一个角,发现剩下的四边形纸片的周长小于原三角形纸片的周长,下列语句能正确解释这一现象的是( )
A、AB>CD B、AB=CD C、AB<CD D、无法确定3. 如图,小红将三角形纸片沿虚线剪去一个角,发现剩下的四边形纸片的周长小于原三角形纸片的周长,下列语句能正确解释这一现象的是( ) A、四边形的周长小于三角形周长 B、两点确定一条直线 C、折线比线段长 D、两点之间线段最短4. 下列说法中不正确的是( )A、若点C在线段AB的延长线上,则AC>AB B、若点C在线段AB上,则AC<AB C、若点C在直线AB上,则AC>AB D、若A,B,C三点不在一条直线上,可能AC=AB5. 如图所示,某同学的家在P处,他想尽快赶到附近C处搭顺风车,他选择第②条路线,用几何知识解释其道理正确的是( )
A、四边形的周长小于三角形周长 B、两点确定一条直线 C、折线比线段长 D、两点之间线段最短4. 下列说法中不正确的是( )A、若点C在线段AB的延长线上,则AC>AB B、若点C在线段AB上,则AC<AB C、若点C在直线AB上,则AC>AB D、若A,B,C三点不在一条直线上,可能AC=AB5. 如图所示,某同学的家在P处,他想尽快赶到附近C处搭顺风车,他选择第②条路线,用几何知识解释其道理正确的是( ) A、两点确定一条直线 B、两点之间,直线最短 C、两点之间,线段最短 D、经过一点有无数条直线6. 按语句“画出线段PQ的反向延长线”画图正确的是( )A、
A、两点确定一条直线 B、两点之间,直线最短 C、两点之间,线段最短 D、经过一点有无数条直线6. 按语句“画出线段PQ的反向延长线”画图正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 下列几何图形与相应语言描述相符的有( )
7. 下列几何图形与相应语言描述相符的有( )如图 , 直线、相交于点 如图 , 直线与线段没有公共点如图 , 延长线段 如图 , 直线经过点
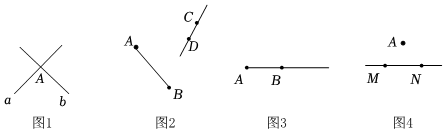 A、个 B、个 C、个 D、个8. 题目;已知:线段a,b.求作:线段AB,使得AB=a+2b.
A、个 B、个 C、个 D、个8. 题目;已知:线段a,b.求作:线段AB,使得AB=a+2b.
小明给出了四个步骤
①在射线AM上画线段AP=a;
②则线段AB=a+2b;
③在射线PM上画PQ=b,QB=b;
④画射线AM.
你认为顺序正确的是( )
A、①②③④ B、④①③② C、④③①② D、④②①③9. 如图,已知∠O ,点 P 为其内一定点,分别在∠O 的两边上找点 A 、 B ,使△ PAB 周长最小的是( )A、.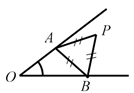 B、
B、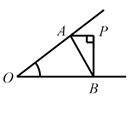 C、
C、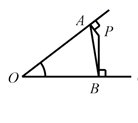 D、
D、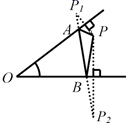 10. 当式子|x+1|+|x﹣6|取得最小值时,x的取值范围为( )A、﹣1≤x<6 B、﹣1≤x≤6 C、x=﹣1或x=6 D、﹣1<x≤6
10. 当式子|x+1|+|x﹣6|取得最小值时,x的取值范围为( )A、﹣1≤x<6 B、﹣1≤x≤6 C、x=﹣1或x=6 D、﹣1<x≤6二、填空题
-
11. 山西省省委,省政府已将“运三高铁”列入山西省“十四五”铁路建设规划,“运三高铁”是穿越中条山的高速铁路,大大减少了人们从运城到三门峡的时间,建造直隧道的目的可以用数学知识解释为12. 下列图中AB<CD的有个
 13. 如图,数轴上点A,B,C表示的数分别为1,﹣ ,﹣3,点D为数轴上一点,则点D到点A,B,C三点距离之和的最小值为 .
13. 如图,数轴上点A,B,C表示的数分别为1,﹣ ,﹣3,点D为数轴上一点,则点D到点A,B,C三点距离之和的最小值为 . 14. 一条笔直的公路上有A,B,C,D四个车站,张大爷要在公路上找到一个位置摆摊,要求摊位到这四个车站距离之和最小,这样的位置可以找到个.
14. 一条笔直的公路上有A,B,C,D四个车站,张大爷要在公路上找到一个位置摆摊,要求摊位到这四个车站距离之和最小,这样的位置可以找到个. 15. 如图所示,AB+CDAC+BD.(填“<”,“>”或“=”)
15. 如图所示,AB+CDAC+BD.(填“<”,“>”或“=”)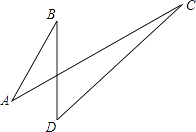 16. 如图,有一种电子游戏,电子屏幕上有一条直线,在直线上有A,B,C,D四点.点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P最多有个.
16. 如图,有一种电子游戏,电子屏幕上有一条直线,在直线上有A,B,C,D四点.点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P最多有个.
三、解答题
-
17. 在图中“O”内标上字母A,B,C,使AC<AB<BC.
 18. 如图1所示,两个村庄A,B在河流l的两侧,现要在河边修建一个水泵站,同时向A、B两村供水,要使所铺设的管道最短,水泵站Р应该建在什么位置?
18. 如图1所示,两个村庄A,B在河流l的两侧,现要在河边修建一个水泵站,同时向A、B两村供水,要使所铺设的管道最短,水泵站Р应该建在什么位置?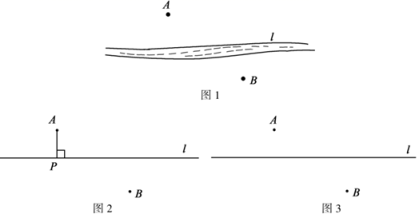
把河流近似看作直线 , 如图2所示.小明提出了这样的方案:过点A作直线的垂线段AP,则点P为水泵站的位置.你同意小明的方案吗?若同意,请说明理由.若不同意,那么你认为水泵站Р应该建在什么位置?请在图3中作出来,并说明依据.
19.(1)、画出数轴,并表示下列有理数:-2, , 1.5;(2)、在(1)的条件下,点O表示0,点A表示-2,点B表示 , 点C表示1.5,点D表示数a,-1<a<0,下列结论:①AO>DO;②BO>DO;③CO>DO.其中一定正确的是(只需填写结论序号).20. 如图,已知平面上有四点 . 用圆规和直尺完成下列作图(不写作法,保留作图痕迹). (1)、连接;并在线段上取一点M , 使点M到点的距离之和最小;(2)、画射线 , 并在射线上取一点N , 使 .21. 如图,已知直线 , 射线 , 线段.
(1)、连接;并在线段上取一点M , 使点M到点的距离之和最小;(2)、画射线 , 并在射线上取一点N , 使 .21. 如图,已知直线 , 射线 , 线段. (1)、用无刻度的直尺和圆规作图:延长到点D,使 , 连接.(2)、比较与的大小,并说明理由.22.
(1)、用无刻度的直尺和圆规作图:延长到点D,使 , 连接.(2)、比较与的大小,并说明理由.22.如图,
(1)一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点B,怎样爬行路线最短?
(2)如果要爬行到顶点C呢?说出你的理由.
 23. 阅读材料.
23. 阅读材料.点M,N在数轴上分别表示数m和n,我们把m,n之差的绝对值叫做点M,N之间的距离,即MN=|m﹣n|.如图,在数轴上,点A,B,O,C,D的位置如图所示,则DC=|3﹣1|=|2|=2;CO=|1﹣0|=|1|=1;BC=|(﹣2)﹣1|=|﹣3|=3;AB=|(﹣4)﹣(﹣2)|=|﹣2|=2.
 (1)、BD=(2)、数轴上表示数x和数-3两点之间的距离可表示为(3)、直接写出方程的解是(4)、小明发现代数式有最小值,最小值是。此时x的值是24. 已知点 都在数轴上,点 为原点,点 对应的数为11,点 对应的数为 , 点 在点 右侧,长度为3个单位的线段 在数轴上移动.
(1)、BD=(2)、数轴上表示数x和数-3两点之间的距离可表示为(3)、直接写出方程的解是(4)、小明发现代数式有最小值,最小值是。此时x的值是24. 已知点 都在数轴上,点 为原点,点 对应的数为11,点 对应的数为 , 点 在点 右侧,长度为3个单位的线段 在数轴上移动. (1)、如图1,当线段 在 两点之间移动到某一位置时,恰好满足线段 , 求此时 的值;(2)、若线段 位于点 的左侧,且在数轴上沿射线 方向移动,当 时,求 的值.
(1)、如图1,当线段 在 两点之间移动到某一位置时,恰好满足线段 , 求此时 的值;(2)、若线段 位于点 的左侧,且在数轴上沿射线 方向移动,当 时,求 的值.