浙江省温州市洞头区2023-2024学年九年级上学期期中数学试卷

试卷更新日期：2023-12-04 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分.每小题只有一个选项是正确的）

1. 已知 $⊙ O$ 的半径为4cm，点P在 $⊙ O$ 上，则 $O P$ 的长为（）

A、2cm B、4cm C、5cm D、8cm

查看试题解析
2. 如图，A是某景区的入口，B，C，D，E是四个不同的出口，小红从A处进入景区，游玩后任选一个出口离开，则她从D出口离开的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
3. 抛物线y=（x﹣2）²+3的顶点坐标是（）

A、（﹣2，3） B、（2，3） C、（﹣2，﹣3） D、（2，﹣3）

查看试题解析
4. 如图，⊙O的半径为10，弦长AB＝16，弦心距OC的长为（）

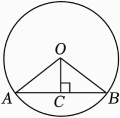A、5 B、6 C、7 D、8

查看试题解析
5. 下列事件中，属于必然事件的是（）

A、在一个只装有黑球的箱子里摸到白球 B、蒙上眼睛射击正中靶心 C、打开电视机，正在播放综艺节目 D、在1个标准大气压下，水加热到100摄氏度沸腾

查看试题解析
6. 在平面直角坐标系中，将二次函数y＝（x-1）²+1的图象向左平移1个单位长度，再向下平移2个单位长度，所得函数的解析式为（）

A、y＝（x-2）²-1 B、y＝（x-2）²+3 C、y＝x²+1 D、y＝x²-1

查看试题解析
7. 如图，AB是⊙O的直径，CD是弦，若∠ABD＝55°，则∠BCD等于（）

A、55° B、45° C、35° D、25°

查看试题解析
8. 已知二次函数y＝-2x²+8x+c的图象位于x轴下方，则c满足的条件是（）

A、c≥8 B、c≥-8 C、c＜8 D、c＜-8

查看试题解析
9. 如图，四边形ABCD内接于⊙O，∠ABC＝∠ADC，BD平分∠ABC．若AB＝3，BC＝4，BD的长为（）

A、4 B、 $\frac{7 \sqrt{2}}{2}$ C、 $\frac{5 \sqrt{3}}{2}$ D、 $\frac{9}{2}$

查看试题解析
10. 已知二次函数y＝﹣（x﹣1）²+10，当m≤x≤n，且mn＜0时，y的最小值为2m，y的最大值为2n，则 $m + n$ 的值为（）

A、3 B、 $\frac{5}{2}$ C、2 D、 $\frac{3}{2}$

查看试题解析

二、填空题（本题有8小题，每小题3分，共24分）

11. 任意抛掷一枚均匀的骰子，骰子各个面的点数分别为1，2，3，4，5，6，则朝上的点数是偶数的概率是．

查看试题解析
12. 二次函数y＝x²﹣2x+3图象与y轴的交点坐标是.

查看试题解析
13. 在一个有2万人的小镇，随意调查了1000人，其中有200人看中央电视台的早间新闻，则该小镇约有人看早间新闻．

查看试题解析
14. 若扇形的圆心角为 $120 °$ ，半径为 $2$ ，则该扇形的面积是（结果保留 $π$ ）．

查看试题解析
15. 已知二次函数y＝ax²+bx+c（a≠0）的部分对应值列表如表：
x
…
-3
0
3
5
…
y
…
7
-8
-5
7
…
则一元二次方程的y＝ax²+bx+c（a≠0）的对称轴为．

查看试题解析
16. 如图，正五边形ABCDE内接于⊙O，则∠ABD＝．

查看试题解析
17. 图1是洞头深门大桥，其桥底呈抛物线，以O为原点，OA所在直线为x轴建立平面直角坐标系（如图2所示），桥面CB∥OA，其抛物线解析式为 $y = - \frac{1}{320} {(x - 80)}^{2} + 20$ ，抛物线上点A离桥面距离AB＝22米，若存在一点E使得 $C E = \frac{3}{8} C B$ ，则点E到抛物线的距离ED＝米．

查看试题解析
18. 图1是某游乐园的摩天轮，A，B两位同学坐在摩天轮上的示意图如图2，摩天轮半径OA为9米，两同学的直线距离AB为6米，当两位同学旋转到同一高度时（A在B的右侧），A同学距离地面的高度为米，当A同学旋转到最高位置，此时两位同学的高度差为米．

查看试题解析

三、解答题（本题有6小题，共46分，解答需写出必要的文字说明、演算步骤或证明过程）

19. 一个不透明的布袋中装有4个只有颜色不同的球，其中有1个黄球、1个白球、2个红球．

(1)、任意摸出1个球，记下颜色后不放回，再任意摸出1个球．求两次摸出的球恰好都是红球的概率（要求画树状图或列表）；

(2)、现再将n个黄球放入布袋，搅匀后，使任意摸出1个球是黄球的概率为 $\frac{1}{2}$ ，求n的值．

查看试题解析
20. 如图，在6×6的正方形网格中，△ABC三个顶点都在格点上，请按要求作图：

(1)、在图1中，将△ABC以点B为旋转中心顺时针旋转90°，得到△DBE．

(2)、在图2中，画一个∠BFC，使得∠BFC＝45°．

查看试题解析
21. 已知抛物线y＝x²-2ax+b经过点A（-2，0），B（0，-8）．

(1)、求抛物线的函数表达式和对称轴：

(2)、抛物线的图象经过点（x₁ ， y₁），（x₂ ， y₂），且x₁＜1，x₁+x₂＞2，求y₁ ， y₂的大小关系．

查看试题解析
22. 如图，以△ABC的一边AB为直径作⊙O交AC于点E，AB＝AC，⊙O与BC边的交点恰好为BC的中点D，连结DE．

(1)、求证：DE＝DC．

(2)、若∠BAC＝45°，AB＝6，求 $\overset{⌢}{D E}$ 的长．

查看试题解析
23. 根据以下素材，探索完成任务，
素材1  图1是中国传统建筑——凉亭，其截面为两个成轴对称的抛物线的一部分（如图2）．凉亭外延水平宽度EC为6米，亭高AO＝4米，在抛物线最低处由一根高为3.1米的柱子支撑，柱子离亭正中心O点距离为2.4米；
素材2  为了美观，拟在凉亭右侧抛物线内悬挂一盏上下长度为0.5米，左右宽度为0.2米的灯笼（如图3），要使得整个灯笼处于右侧且保持离地至少3米的安全距离（灯笼挂钩G位于其中间最上端）.

(1)、任务1  确定凉亭右侧形状：在图2中建立合适的直角坐标系，求凉亭右侧抛物线的函数表达式；

(2)、任务2  探究悬挂位置：在你建立的坐标系中，在安全的前提下，确定灯笼的悬挂水平位置范围.

查看试题解析
24. 如图，
在△ABC中，AB＝BC，∠ABC＝90°，D是AB上一动点，连接CD，以CD为直径的⊙O交AC于点E，连接BO并延长交AC于点F，交⊙O于点G，连接BE，EG．

(1)、求证：BE＝EG．

(2)、当CD平分∠BCA时，求证：△BEF为等腰三角形．

(3)、当BD＝CF，请直接写出△COF和△BOD的面积之比为．

查看试题解析

x	…	-3	0	3	5	…
y	…	7	-8	-5	7	…