浙江省杭州市拱墅区2023-2024学年五校联考八年级上学期期中数学试卷
试卷更新日期：2023-12-04 类型：期中考试
一、选择题（本题有10小题，每小题3分，共30分，每个小题给出的四个选项中只有一个是符合题目要求的）
-
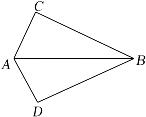
1. 下列数学符号中，是轴对称图形的是（ ）A、∥ B、⊥ C、≌ D、≠2. 对于命题“若a＞b，则|a|＞|b|”，能说明它是假命题的反例是（ ）A、a＝3，b＝2 B、a＝3，b＝4 C、a＝-3，b＝-2 D、a＝2，b＝-23. 如图，∠CAB＝∠DAB，那么添加下列一个条件后，仍无法判定△ABC≌△ABD的是（ ）
A、∠ABC＝∠ABD B、BC＝BD C、∠C＝∠D D、AC＝AD4. 若x＜3，则（ ）A、x-2＞0 B、2x＞-1 C、2x＜3 D、18-3x＞05. 已知等腰三角形的两边长为x、y，且满足|x-4|+（x-y+4）2＝0，则三角形的周长为（ ）A、12 B、16 C、20 D、16或206. 在△ABC中，它的三边分别为a，b，c，下列条件：①∠A+∠B＝∠C；②∠A＝∠B＝2∠C；③∠A：∠B：∠C＝3：4：5；④a：b：c＝1：：；其中，能确定△ABC是直角三角形的条件有（ ）A、1个 B、2个 C、3个 D、4个7. 若不等式组的解集为1＜x＜2，则（m+n）2022的值为（ ）A、-1 B、0 C、1 D、28. 如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，E为对角线AC的中点，连接BE，ED，BD，若∠BAD＝58°，则∠EBD的度数为（ ）度.
A、29 B、32 C、45 D、649. 如图，在△ABC中，∠ACB＝90°，AC＜BC.分别以点A、B为圆心，大于AB的长为半径画弧，两弧交于D，E两点，直线DE交BC于点F，连接AF.以点A为圆心，AF为半径画弧，交BC延长线于点H，连接AH.若BC＝4，则△AFH的周长为（ ）
A、8 B、6 C、4 D、10. 如图，在 中， ， ，D，E分别为线段AB，AC上一点，且 ，连接BE、CD交于点G，延长AG交BC于点F.以下四个结论正确的是（ ）
① ；②若 ，则 ；③若BE平分 ，则 ；④连结EF，若 ，则 .
A、①②③ B、③④ C、①②④ D、①②③④二、填空题（本题有6小题，每小题4分，共24分）
-
11. 若m与7的和是正数，则可列出不等式 .12. 已知直角三角形的两边的长分别是3和4，则第三边长为 ．13. 不等式组的解集为x＞2，则a的取值范围是 ．14. 在同一平面内，有相互平行的三条直线a，b，c，且a，b之间的距离为1，b，c之间的距离是2，若等腰Rt△ABC的三个顶点恰好各在这三条平行直线上，如图所示，∠BAC＝90°，在△ABC的面积是.
15. 如图，在△ABC中，∠ACB＝90°，∠B-∠A＝10°，D是AB上一点，将△ACD沿CD翻折后得到△CED，边CE交AB于点F.若△DEF中有两个角相等，则∠ACD＝.
16. 在△ABC中，∠C＝90°，AC＝6，BC＝8，将它的一个锐角翻折，使该锐角顶点落在其对边的中点D处，折痕交另一直角边于点E，交斜边于点F，则DE的长为.三、解答题（共7小题，共66分）
-
17. 解下列一元一次不等式（组）：(1)、5x≥3x+1；(2)、 ， 并把它的解集表示在数轴上．18. 如图，
在边长为1个单位长度的小正方形组成的网格中，点A、B、C在小正方形的顶点上．
(1)、画出与△ABC关于直线l成轴对称的△A′B′C′；(2)、求△ABC的面积．19. 如图，点C、E、B、F在一条直线上，AB⊥CF于B，DE⊥CF于E，AC＝DF，AB＝DE.求证：CE＝BF.
20. 如图，在△ABC中，D为AB上一点，E为AC中点，连接DE并延长至点F，使得EF＝ED，连CF.
(1)、求证：CF∥AB(2)、若∠ABC＝50°，连接BE，BE平分∠ABC，AC平分∠BCF，求∠A的度数.21. 如图，在锐角△ABC中，点E是AB边上一点，BE＝CE，AD⊥BC于点D，AD与EC交于点G．
(1)、若BE＝10，CD＝3，G为CE中点，求AG的长；(2)、求证：△AEG是等腰三角形．22. 如图1，在△ABC中，BO⊥AC于点O，AO＝BO＝3，OC＝1，过点A作AH⊥BC于点H，交BO于点P．
(1)、求线段OP的长度；(2)、连接OH，求证：∠OHP＝45°；(3)、如图2，若点D为AB的中点，点M为线段BO延长线上一动点，连接MD，过点D作DN⊥DM交线段OA延长线于N点，则S△BDM-S△ADN的值是否发生改变，如改变，求出该值的变化范围；若不改变，求该式子的值．