广东省深圳市2023-2024学年八年级上学期数学期中试卷
试卷更新日期:2023-12-04 类型:期中考试
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 下列各数中,是无理数的是( )A、0 B、 C、π D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,小手盖住的点的坐标可能为( )
 A、(5,2) B、(-3,-3) C、(-6,4) D、(2,-5)4. 已知点P(-3,5),则点P到y轴的距离是( )A、5 B、3 C、4 D、-35. 函数y=中,自变量x的取值范围是( )A、x>2 B、1≤x<2 C、1<x<2 D、1<x≤26. 已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件中不能判断△ABC是直角三角形的是( )A、∠A=∠C-∠B B、a2=b2-c2 C、a=3,b=5,c=4 D、a:b:c=2:3:47. 已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2023的值为( )A、0 B、-1 C、1 D、-320238. 如图,圆柱形玻璃杯高为11cm,底面周长为30cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处爬行到内壁B处的最短路线长为(杯壁厚度不计)( )
A、(5,2) B、(-3,-3) C、(-6,4) D、(2,-5)4. 已知点P(-3,5),则点P到y轴的距离是( )A、5 B、3 C、4 D、-35. 函数y=中,自变量x的取值范围是( )A、x>2 B、1≤x<2 C、1<x<2 D、1<x≤26. 已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件中不能判断△ABC是直角三角形的是( )A、∠A=∠C-∠B B、a2=b2-c2 C、a=3,b=5,c=4 D、a:b:c=2:3:47. 已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2023的值为( )A、0 B、-1 C、1 D、-320238. 如图,圆柱形玻璃杯高为11cm,底面周长为30cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处爬行到内壁B处的最短路线长为(杯壁厚度不计)( ) A、12cm B、17cm C、20cm D、25cm9. 一次函数y=kx+k2(k<0)的图象大致是( )A、
A、12cm B、17cm C、20cm D、25cm9. 一次函数y=kx+k2(k<0)的图象大致是( )A、 B、
B、 C、
C、 D、
D、 10. 如图所示,直线y=x+3分别与x轴、y轴交于点A、B,若∠ABC=45°,则直线BC的函数表达式为( )
10. 如图所示,直线y=x+3分别与x轴、y轴交于点A、B,若∠ABC=45°,则直线BC的函数表达式为( )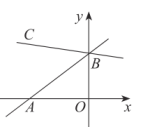 A、y=x+3 B、y=x+3 C、y=x+3 D、y=x+3
A、y=x+3 B、y=x+3 C、y=x+3 D、y=x+3二、填空题(本大题共5小题,每小题3分,共15分)
-
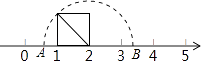
11. 若a,b为两个连续整数,且 , 则.12. y=(m-1)x|m|+3是关于x的一次函数,则m=.13. 如图,以数轴的单位长度线段为边长作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是 .
 14. 对实数a、b,定义“★”运算规则如下:a★b= , 则★(★)= .15. 如图,直线y=x+2与x轴、y轴分别交于点B和点A,点C是线段OA上的一点,若将△ABC沿BC折叠,点A恰好落在x轴上的A'处,则△BOC的面积为.
14. 对实数a、b,定义“★”运算规则如下:a★b= , 则★(★)= .15. 如图,直线y=x+2与x轴、y轴分别交于点B和点A,点C是线段OA上的一点,若将△ABC沿BC折叠,点A恰好落在x轴上的A'处,则△BOC的面积为.
三、解答题(本大题共7小题,共55分)
-
16. 计算:(1)、 ;(2)、 .17. 已知的整数部分是a,小数部分是b.(1)、a= , b= .(2)、试求b2020(a+)2021的值.18. 如图所示,在平面直角坐标系中,已知A(2,2),B(-2,0),C(-1,-2).
 (1)、在平面直角坐标系中画出△ABC;(2)、若点D与点C关于y轴对称,则点D的坐标为(3)、求△ABC的面积;(4)、已知点P为x轴上一点,若S△ABP=6,求点P的坐标.19. 某教育科技公司销售A,B两种多媒体,这两种多媒体的进价与售价如表所示:
(1)、在平面直角坐标系中画出△ABC;(2)、若点D与点C关于y轴对称,则点D的坐标为(3)、求△ABC的面积;(4)、已知点P为x轴上一点,若S△ABP=6,求点P的坐标.19. 某教育科技公司销售A,B两种多媒体,这两种多媒体的进价与售价如表所示:A
B
进价(万元/套)
3
2.4
售价(万元/套)
3.3
2.8
(1)、若该教育科技公司计划购进两种多媒体共50套,共需资金132万元,该教育科技公司计划购进A,B两种多媒体各多少套?(2)、若该教育科技公司计划购进两种多媒体共50套,其中购进A种多媒体m套(10<m<20),当把购进的两种多媒体全部售出,求购进A种多媒体多少套时,能获得最大利润,最大利润是多少万元?20. 将一长方形纸片ABCD折叠,使顶点A与C重合,折痕为EF.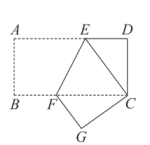 (1)、试说明CE=CF;(2)、若AB=4,BC=8,求DE的长.21. 兄妹俩放学后沿图1中的马路从学校出发,到书吧看书后回家.哥哥步行先出发,途中速度保持不变:妹妹骑车,到书吧前的速度为200米/分.图2中的图象分别表示两人离学校的路程s(米)与哥哥离开学校的时间t(分)的函数关系.
(1)、试说明CE=CF;(2)、若AB=4,BC=8,求DE的长.21. 兄妹俩放学后沿图1中的马路从学校出发,到书吧看书后回家.哥哥步行先出发,途中速度保持不变:妹妹骑车,到书吧前的速度为200米/分.图2中的图象分别表示两人离学校的路程s(米)与哥哥离开学校的时间t(分)的函数关系.
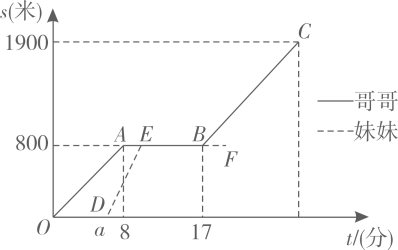 (1)、求哥哥步行的速度.(2)、已知妹妹比哥哥迟2分钟到书吧.
(1)、求哥哥步行的速度.(2)、已知妹妹比哥哥迟2分钟到书吧.
①求图中a的值;
②妹妹在书吧待了10分钟后回家,速度是哥哥的1.6倍,能否在哥哥到家前追上哥哥?若能,求追上时兄妹俩离家还有多远;若不能,说明理由.22. 如图1,在平面直角坐标系xOy中,直线l1:y=x+1与x轴交于点A,直线l2:y=3x-3.与x轴交于点B,与l1相交于点C. (1)、请直接写出点A、点B、点C的坐标:A , B , C(2)、如图2,动直线y=t分别与直线l1 , l2交于P,Q两点.
(1)、请直接写出点A、点B、点C的坐标:A , B , C(2)、如图2,动直线y=t分别与直线l1 , l2交于P,Q两点.①若PQ=3,求t的值.
②若存在S△AQC:S△ABC=3:4,求出此时点Q的坐标;若不存在,请说明理由.