浙江省初中名校发展共同体2023-2024学年八年级上学期数学11月期中试卷

试卷更新日期：2023-12-04 类型：期中考试

进入出卷网下载

一、选择题(本大题共10个小题，每题3分，共30分)

1. 下列图形中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若a<b，则下列结论成立的是（）

A、a+2>b+2 B、-2a<-2b C、3a>3b D、1-a>1-b

查看试题解析
3. 在△ABC中，作BC边上的高(图中虚线)，、下列作法正确的是（）

A、 B、 C、 D、

查看试题解析
4. 下列可以作为命题“若x>y，则x²>y²”是假命题的反例是（）

A、x=-2，y=-1 B、x=2，y=-1 C、x=1，y=-2 D、x=2，y=1

查看试题解析
5. 若等腰三角形的两条边长为2和5，则这个等腰三角形的周长为（）

A、12 B、9 C、12或9 D、7或15

查看试题解析
6. 如图，在△ABC中，在边AB上取一点P，连结CP，在边CP上取一点Q，连结BQ．若△ACP≌△QBP，∠ACP=23°，则∠CBQ的度数为（）

A、23° B、22° C、30° D、32°

查看试题解析
7. 在△ABC中，它的三边分别为a，b，c，下列条件：①∠A= $\frac{1}{2}$ ∠B= $\frac{1}{3}$ ∠C，②∠A=∠B-∠C，③∠A：∠B：∠C=3：4：5，④a：b：c=2：3： $\sqrt{5}$ 其中，能确定△ABC是直角三角形的条件为（）

A、②③④ B、①③④ C、①②④ D、①②③

查看试题解析
8. 如图，已知钝角三角形ABC，按以下步骤尺规作图，并保留作图痕迹．
步骤1：以C为圆心，CB为半径画弧①；
步骤2：以A为圆心，AB为半径画弧②，交弧①于点D；
步骤3：连结BD，交AC的延长线于点E．
下列叙述正确的是（）

A、BC平分∠ABD B、AB=BD C、AE=BD D、BE=DE

查看试题解析
9. 若关于x的不等式组 ${\begin{cases} 2 x - 1 \geq 5 \\ x < 2 a - 1 \end{cases}$ 的整数解共有四个，则a的取值范围是（）

A、3.5<a≤4 B、3.5≤a<4 C、3.5<a<4 D、3.5≤a≤4

查看试题解析
10. 如图1，以直角三角形的各边分别向外作正方形，再把较小的两个正方形按图2的方式放置在大正方形内，记四边形ABCD面积为S₁ ，四边形CDEG的面积为S₂ ，四边形GFKH的面积为S₃ ，四边形CGHP的面积为S₄ ，若知道图中阴影部分的面积，则一定能求出（）

A、S₁ B、S₂ C、S₃ D、S₄

查看试题解析

二、填空题(本大题有6个小题，每题4分，共24分)

11. 命题“直角三角形的两个锐角互余”的逆命题为．

查看试题解析
12. 如图，B、E、C、F四点在同一直线上，且BE=CF，AC=DF，添加一个条件，使△ABC≌△DEF(写出一个即可)．

查看试题解析
13. 已知三角形的三边长分别为3，5和2x-1，则整数x的最大值为.

查看试题解析
14. 如图，Rt△ABC中，∠C=90°，AC=8，BC=6．有一动点P从点C开始沿C→B→A方向以2cm/s的速度运动到点A后停止运动，当运动时间为秒时，△ACP是等腰三角形．

查看试题解析
15. 如图，在△ABC中，AC=8，BC=15，AB=17，AD平分∠CAB，则△ABD的面积为。

查看试题解析
16. 如图，△ABC为等腰直角三角形，∠ABC=90°，点P在AC的延长线上，且AC=CP=4，将△ABC沿AB方向平移得到△A'B'C'，连结PA'，PC'，则△PA'C'的周长的最小值为.

查看试题解析

三、解答题(本大题有8个小题，第17~19每小题6分，第20，21每小题8分，第22，23每小题10分第24题12分，共66分)

17. 解不等式 $\frac{1 + x}{2} \leq \frac{1 + 2 x}{3} + 1$ ，并把解在数轴上表示出来．

查看试题解析
18. 如图，AB与CD相交于点O，AB=CD，∠BAD=∠DCB=90°．求证：OB=OD．

查看试题解析
19. 如图，在8×8的方格纸中，△ABC的三个顶点都在格点上，仅用无刻度的直尺，按要求作图．

(1)、在图1中，画出所有与△ABC全等(不包含△ABC)的△ABP．

(2)、在图2中，过顶点A画一条直线平分△ABC的面积(不写作法，保留作图痕迹)．

查看试题解析
20. 对于任意两个实数a，b，探究a²+b²与2ab的大小关系：

(1)、尝试：(用“>”，“=”或“<”填空)
①3²+5²2×3×5；
②(-3)²+5²2×(-3)×5；
③(-3)²+(-3)²2×(-3)×(-3)；
④( $\frac{3}{2}$ )²+( $\frac{1}{4}$ )²2× $\frac{3}{2}$ × $\frac{1}{4}$

(2)、归纳：对于任意实数a和b，a²+b²与2ab有怎样的大小关系，并说明理由．

查看试题解析
21. 如图，在线段AB的同侧作△PAB和△QAB，PB和QA相交于点O，M、N分别是边AQ、BP的中点，连结PQ，PM，MN，∠APQ=∠ABQ=90°．

(1)、判断△PMN的形状，并说明理由；

(2)、当AQ=26，BP=24时，求MN的长．

查看试题解析
22. 污水治理，保护环境，某市治污公司决定购买A，B两种型号污水处理设备共12台，已知A，B两种型号的设备，每台的价格，月处理污水量如表：

A型
B型
价格(万元/台)
a
b
处理污水量(吨/月)
220
180
经调查：购买一台A型设备比购买一台B型设备多3万元，购买1台A型设备比购买3台B型设备少3万元．

(1)、求a，b的值；

(2)、经预算：市治污公司购买污水处理设备的资金不超过50万元，你认为该公司有哪几种购买方案

(3)、在(2)问的条件下，若每月要求处理的污水量不低于2260吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．

查看试题解析
23. 如图①，在△ABC中，沿∠BAC的平分线AB₁折叠，剪掉重复部分；将余下部分沿∠B₁A₁C的平分线A₁B₂折叠，剪掉重复部分……将余下部分沿∠B_nA_nC的平分线A_nB_n+1折叠，点B_n与点C重合，无论折叠多少次，只要最后一次恰好重合，则称∠BAC是△ABC的好玩角．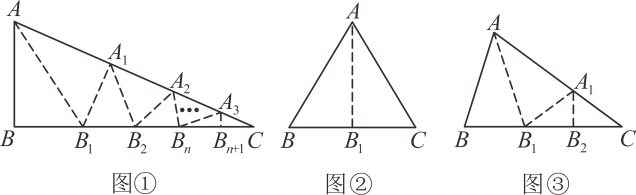
小马展示了确定∠BAC是△ABC的好玩角的两种情形．
情形一：如图②，沿等腰三角形ABC顶角∠BAC的平分线AB₁折叠，点B与点C重合；
情形二：如图③，沿∠BAC的平分线AB₁折叠，剪掉重复部分；将余下部分沿∠B₁A₁C的平分线A₁B₂折叠，此时点B₁与点C重合．

(1)、探究发现：
在△ABC中，∠B=66°，∠B>∠C，经过两次折叠，∠BAC是△ABC的好玩角，求∠C的度数．

(2)、小马经过三次折叠发现了∠BAC是△ABC的好玩角，请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系为．根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好玩角，则∠B与∠C(不妨设∠B>∠C)之间的等量关系为．

(3)、应用提升：
小马找到一个三角形，三个角分别为20°，60°，100°，发现60°和100的两个角都是此三角形的好玩角．请你完成，如果一个三角形的最小角是18°试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好玩角．

查看试题解析
24. 已知，点M为线段AB的中点，点P为线段AB上一动点，过点P作直线l(不与AB重合)，AE⊥l于．点E，BF⊥I于点F．

(1)、如图1，当点P与点M重合时，EM与FM有怎样的数量关系，并说明理由；

(2)、如图2，当点P不与点M重合时，(1)问中的结论是否仍然成立，为什么？

(3)、在等边△ABC中，点M为AB的中点，点P为AB边上一动点，过点P的直线l∥BC，AE⊥I于点E，BF⊥l于点F，连结BE．
①如图3，当AE=BE时，求∠MFE的度数．
②如图4，当∠MFE=45°时，探究PM、PB、PE的数量关系，并说明理由．

查看试题解析

	A型	B型
价格(万元/台)	a	b
处理污水量(吨/月)	220	180