浙江省初中名校发展共同体2023-2024学年九年级上学期数学11月期中试卷

试卷更新日期：2023-12-04 类型：期中考试

进入出卷网下载

一、选择题(本大题共10题，每小题3分，共30分。每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分)

1. 若 $\frac{a}{b} = \frac{4}{3}$ ，则 $\frac{a - b}{b}$ 的值等于（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、 $\frac{7}{3}$ D、 $- \frac{7}{3}$

查看试题解析
2. 已知在Rt△ABC中，∠C=90°，AC=5，BC=12，则△ABC的外接圆直径为（）

A、5 B、12 C、13 D、6.5

查看试题解析
3. 若将函数y=3x²的图象向右平移2个单位，再向上平移4个单位，得到的抛物线表达式为（）

A、y=3(x+2)²-4 B、y=3(x+2)²+4 C、y=3(x-2)²-4 D、y=3(x-2)²+4

查看试题解析
4. 简车是我国古代发明的一种水利灌溉工具，彰显了我国古代劳动人民的智慧，如图1，点P表示简车的一个盛水桶．如图2，当简车工作时，盛水桶的运行路径是以轴心0为圆心，5m为半径的圆，且圆心在水面上方．若圆被水面截得的弦AB长为8m，则简车工作时，盛水桶在水面以下的最大深度为（）m．

A、1 B、2 C、3 D、4

查看试题解析
5. 关于二次函数y=(x+2)²-4，下列说法正确的是（）

A、函数图象的开口向下 B、函数图象的顶点坐标是(2，-4) C、该函数的最大值是-4 D、当x≥-2时，y随x的增大而增大

查看试题解析
6. 如图，△ABC中，∠A=90°，AB=6，BC=10，∠ABC的平分线交AC于点D，与BC的垂线CE相交于点E，过点D作DF⊥BC于点F，则BD：DE为（）

A、3：2 B、5：3 C、4：3 D、2：1

查看试题解析
7. 小舟给出如下题目：二次函数y=ax²+bx+c(a≠0)的图象如图所示，点A坐标为(-1，0)，给出下列结论：①b+2a<0；②b²-4ac<0；③x=3是方程ax²+bx+c=0(a≠0)的其中一个解；④3a+b>0；其中正确的是（）

A、① B、② C、③ D、④

查看试题解析
8. 如图，点A，B，C，D为⊙O上的四个点，AC平分∠BAD，AC交BD于点E，CE=2，CD=3，则AC的长为（）

A、4 B、4.5 C、5 D、5.5

查看试题解析
9. 如图，已知△ABC，O为AC上一点，以OB为半径的圆经过点A，且与BC、OC交于点D、E，设∠A=α，∠C=β，（）

A、若α+β=70°，则 $\overset{⌢}{D E}$ 的度数为20° B、若α+β=70°，则 $\overset{⌢}{D E}$ 的度数为40° C、若α-β=70°，则 $\overset{⌢}{D E}$ 的度数为20° D、若α-β=70°，则 $\overset{⌢}{D E}$ 的度数为40°

查看试题解析
10. 定义平面内任意两点P(x₁ ， y₁)、Q(x₂ ， y₂)之间的距离d_PQ=|x₂-x₁|+|y₂-y₁|称为这两点间的曼哈顿距离(简称为曼距)．例如，在平面直角坐标系中，点P(-3，-2)与点Q(2，2)之间的曼距d_PQ=|-3-2|+|-2-2|=5+4=9，若点A在直线y= $\frac{1}{2}$ x-2上，点B为抛物线y=x²+2x上一点，则曼距d_AB的最小值（）

A、 $\frac{23 \sqrt{5}}{40}$ B、 $\frac{69}{40}$ C、 $\frac{23}{16}$ D、 $\frac{3}{2}$

查看试题解析

二、填空题(本题有6小题，每小题4分，共24分)

11. 请写出一个开口向下并且顶点在y轴上的二次函数表达式．

查看试题解析
12. 生活中到处可见黄金分割的美．如图，在设计人体雕像时，使雕像的腰部以下a与全身b的高度比值接近0.618，可以增加视觉美感．若图中b为4米，则a约为.米．(结果精确到一位小数)

查看试题解析
13. 二次函数y=a(x+5)(x-3)的图象如图所示，当y>0时，x的取值范围是.

查看试题解析
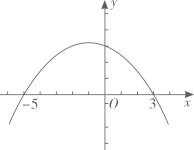14. 如图，在扇形EOF中放置有三个全等的矩形方格，点O为扇形的圆心，格点A、B、C分别在扇形的两条半径和弧上，已知每个矩形方格的长和宽分别为 $\sqrt{3}$ 和1，则阴影部分的面积为.

查看试题解析
15. 如图，矩形纸片ABCD，点E在边AD上，连接BE，点F在线段BE上，且EF= $\frac{1}{3}$ BF，折叠矩形纸片使点C恰好落在点F处，折痕为DG，若AB=4，则折痕DG的长为.

查看试题解析
16. 量角器和三角板是我们平常数学学习中常用的工具．有一天，爱思考的小聪拿着两块工具拼成了如图1的样子，计划让三角板的直角顶点始终在量角器的半圆弧上运动，紧接着小聪根据自己的想法画出了示意图(如图2)。已知点C是量角器半圆弧的中点，点P为三角板的直角顶点，两直角边PE、PF分别过点A、B．连结CP，过点O作OM⊥CP交CP于点M，交AP于点N若AB=8，则NB的最小值为；若点Q为 $\overset{⌢}{B C}$ 的中点，则点P从点Q运动到点B时，N点的运动路径长为.

查看试题解析

三、解答题(本题有8小题，第17~19题每小题6分，第20、21题每小题8分，第22、23题每小题10分，第24题12分，共66分)

17. 已知线段a、b、c满足a：b：c=3：2：4，且a+2b+c=11．

(1)、求a、b、c的值；

(2)、若线段x是线段a、b的比例中项，求x的值．

查看试题解析
18. 如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．

(1)、若∠B=70°，求∠CAD的度数；

(2)、若AB=13，AC=12，求DE的长．

查看试题解析
19. 已知二次函数y=x²-2x+3，当-2≤x≤2时，求函数y的取值范围．
小胡同学的解答如下：
解：当x=-2时，则y=(-2)²-2×(-2)+3=11；
当x=2时，则y=2²-2×2+3=3；
所以函数y的取值范围为3≤y≤11．
小胡的解答正确吗？如果正确，请在方框内打“√”：如果错误，请在方框内打“×”，并写出正确的解答过程．

查看试题解析
20. 请用无刻度的直尺在以下两个图中画出线段BC的垂直平分线(保留作图痕迹，不写作法)

(1)、如图①，等腰△ABC内接于⊙O中，AB=AC；

(2)、如图②，已知四边形ABCD为矩形，点A、D在圆上，AB、CD与⊙O分别交于点E、F．

查看试题解析
21. 杭州亚运会期间，某网店经营亚运会吉祥物“宸宸、琮琮和莲莲”钥匙扣礼盒装，每盒进价为30元，出于营销考虑，要求每盒商品的售价不低于30元且不高于38元，在销售过程中发现该商品每周的销售量y(件)与销售单价x(元)之间满足一次函数关系；当销售单价为32元时，销售量为36件；当销售单价为34元时，销售量为32件，

(1)、请求出y与x的函数关系式；

(2)、设该网店每周销售这种商品所获得的利润为w元，
①写出w与x的函数关系式；
②将该商品销售单价定为多少元时，才能使网店每周销售该商品所获利润最大？最大利润是多少？

查看试题解析
22. 如图1，在正方形ABCD中， $\frac{C E}{D E} = \frac{1}{2}$ ， F为BE上的一点，连结CF并延长交AB于点M，作MN⊥CM交边AD于点N．

(1)、当F为BE中点时，求证：AM=2CE；

(2)、如图2，若 $\frac{E F}{B F} = \frac{2}{3}$ ，求 $\frac{A N}{N D}$ 的值．

查看试题解析

23. 根据以下素材，探索完成任务．

绿化带灌溉车的操作方案

素材1	辆绿化带灌溉车正在作业，水从喷水口喷出，水流的上下两边缘可以抽象为两条抛物线的一部分：喷水口离开地面高1.6米，上边缘抛物线最高点离喷水口的水平距离为3米，高出\|喷水口0.9米，下边缘水流形状与上边缘相同，且喷水口是最高点。
素材2	路边的绿化带宽4米
素材3	绿化带正中间种植了行道树，为了防治病虫害、增加行道树的成活率，园林工人给树木“打针”。针一般打在离地面1.5米到2米的高度(包含端点)。

问题解决

(1)、任务1：确定上边缘水流形状

建立如图所示直角坐标系，求上边缘抛物线的函数表达式．

(2)、任务2：探究灌溉范围

灌溉车行驶过程中喷出的水能浇浓到整个绿化带吗？请说明理由．

(3)、任务3：拟定设计方案

灌溉时，发现水流的上下两边缘冲击力最强，喷到针筒容易造成针筒脱落。那么请问在满足最大灌溉面积的前提下对行道树“打针”是否有影响，并说明理由；若你认为有影响，请给出具体的“打针”范围。

查看试题解析

24. 如图1，△ABC是⊙O内接三角形将△ABC绕点A逆时针旋转至△AED，其中点D在圆上，点E在线段AC上．

(1)、求证：DE=DC；

(2)、如图2，过点B作BF∥CD分别交AC、AD于点M、N，交⊙O于点F，连结AF．求证：AN·DE=AF·BM：

(3)、在(2)的条件下，若 $\frac{A B}{A C} = \frac{1}{3}$ 时，求 $\frac{B F}{B C}$ 的值．

查看试题解析