河北省承德市兴隆县2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-04 类型:期中考试
一、选择题(本大题共16个小题,1-6每小题3分,7-16每小题2分,共38分,在每个小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 已知 , 则下列等式不成立的是( )A、 B、 C、 D、2. 在 中,∠C= ,AB=4, ,则 的长为( )A、3 B、2 C、 D、3. 以为一根的一元二次方程可能是( )A、 B、 C、 D、4. 用配方法解方程 , 则配方正确的是( )A、 B、 C、 D、5. 已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
 A、
A、 B、
B、 C、
C、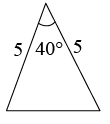 D、
D、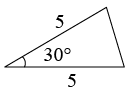 6. 如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则 tan∠ACB的值为 ( )
6. 如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则 tan∠ACB的值为 ( ) A、1 B、 C、 D、7. 下列一元二次方程中,没有实数根的是( )A、 B、 C、 D、8. 根据关于x的一元二次方程 , 可列表如下:则方程的正数解满足( )
A、1 B、 C、 D、7. 下列一元二次方程中,没有实数根的是( )A、 B、 C、 D、8. 根据关于x的一元二次方程 , 可列表如下:则方程的正数解满足( )x
2.5
3
3.1
3.2
3.3
3.4
0.29
0.76
A、解的整数部分是3,十分位是1 B、解的整数部分是3,十分位是2 C、解的整数部分是3,十分位是3 D、解的整数部分是3,十分位是49. 如图, , 那么下列结论正确的是( ) A、 B、 C、 D、10. 关于x的一元二次方程的一个根是1,则另一个根和m的值分别为( )A、 , 3 B、1,3 C、 , 4 D、3,11. 如图,身高的小亮站在某路灯下,发现自己的影长恰好是 , 经测量,此时小亮离路灯底部的距离是 , 则路灯离地面的高度AB是( )
A、 B、 C、 D、10. 关于x的一元二次方程的一个根是1,则另一个根和m的值分别为( )A、 , 3 B、1,3 C、 , 4 D、3,11. 如图,身高的小亮站在某路灯下,发现自己的影长恰好是 , 经测量,此时小亮离路灯底部的距离是 , 则路灯离地面的高度AB是( )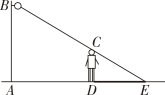 A、 B、 C、 D、12. 如图,P是叶脉AB的黄金分割点(),则( )
A、 B、 C、 D、12. 如图,P是叶脉AB的黄金分割点(),则( )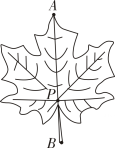 A、 B、 C、 D、13. 如图,一座厂房屋顶人字架的跨度 , 上弦 , , 若用科学计算器求上弦AB的长,则下列按键顺序正确的是( )
A、 B、 C、 D、13. 如图,一座厂房屋顶人字架的跨度 , 上弦 , , 若用科学计算器求上弦AB的长,则下列按键顺序正确的是( ) A、 B、 C、 D、14. 如图,在直角坐标系中,与是位似图形,已知点 , 则位似中心的坐标是( )
A、 B、 C、 D、14. 如图,在直角坐标系中,与是位似图形,已知点 , 则位似中心的坐标是( )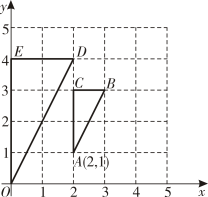 A、 B、 C、 D、15. 为增强同学们的体质,丰富校园文化体育生活,某校八年级举行了篮球比赛,比赛以循环赛的形式进行,即每个班级之间都要比赛一场,共比赛了45场.该校八年级共有( )个班.A、9 B、10 C、5 D、816. 如图,是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是的面积的( )
A、 B、 C、 D、15. 为增强同学们的体质,丰富校园文化体育生活,某校八年级举行了篮球比赛,比赛以循环赛的形式进行,即每个班级之间都要比赛一场,共比赛了45场.该校八年级共有( )个班.A、9 B、10 C、5 D、816. 如图,是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是的面积的( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共3个小题,5个空,每空2分,共10分。)
-
17. 已知关于x的一元二次方程 .
⑴若方程的一个根为 , 则a的值为;
⑵若方程有实数根,则满足条件的正整数a的值为 .
18. 如图所示,在中, , 于D , 下列四个结论中:①;②;③;④ .
其中正确的有 . (填序号)
 19. 如图,河堤横断面迎水坡AB的坡度是 , , 则 , 坡面AB的长度是 .
19. 如图,河堤横断面迎水坡AB的坡度是 , , 则 , 坡面AB的长度是 .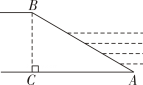
三、解答题(本大题共7个小题,共72分。解答应写出文字说明、证明过程或演算步骤)
-
20. 解方程:(1)、(2)、21. 如图,在等边中,点D、E分别在边BC、AC上, , 若 , , 求DE的长.
 22. 如图,有总长为24米的篱笆,一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的长方形花圃ABCD .
22. 如图,有总长为24米的篱笆,一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的长方形花圃ABCD . (1)、如果设花圃的宽米,则BC长多少米?(用含x的代数式表示)(2)、如果要使花圃的面积为45平方米,那么花圃的宽AB应为多少米?23. 如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是 , 朝大树方向下坡走8米到达坡底A处,在A处测得大树顶端B的仰角是 , 若坡角 , 求大树的高度(结果保留整数,参考数据: , , , )
(1)、如果设花圃的宽米,则BC长多少米?(用含x的代数式表示)(2)、如果要使花圃的面积为45平方米,那么花圃的宽AB应为多少米?23. 如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是 , 朝大树方向下坡走8米到达坡底A处,在A处测得大树顶端B的仰角是 , 若坡角 , 求大树的高度(结果保留整数,参考数据: , , , ) 24. 我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用.例如:已知可取任何实数,试求二次三项式的最小值.
24. 我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用.例如:已知可取任何实数,试求二次三项式的最小值.解:;
∵无论x取何实数,都有 ,
∴ , 即的最小值为2.
(1)、【尝试应用】请直接写出的最小值;(2)、【拓展应用】试说明:无论x取何实数,二次根式都有意义;(3)、【创新应用】如图,在四边形ABCD中, , 若 , 求四边形ABCD的面积最大值. 25. 某超市于今年年初以每件25元的进价购进一批商品当商品售价为40元时,一月份销售256件二、三月该商品十分畅销销售量持续走高在售价不变的基础上,三月底的销售量达到400件设二、三这两个月的月平均增长率不变.(1)、求二、三这两个月的月平均增长率;(2)、从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价1元,销售量增加5件,当商品降价多少元时,商场获利4250元?26. 如图1和图2,平面上,四边形ABCD中, , , , , , 点M在AD上,且 . 将线段MA绕点M顺时针旋转到 . 的平分线MP所在的直线交折线于点P , 设点P在该折线上运动的路径长为 , 连接 .
25. 某超市于今年年初以每件25元的进价购进一批商品当商品售价为40元时,一月份销售256件二、三月该商品十分畅销销售量持续走高在售价不变的基础上,三月底的销售量达到400件设二、三这两个月的月平均增长率不变.(1)、求二、三这两个月的月平均增长率;(2)、从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价1元,销售量增加5件,当商品降价多少元时,商场获利4250元?26. 如图1和图2,平面上,四边形ABCD中, , , , , , 点M在AD上,且 . 将线段MA绕点M顺时针旋转到 . 的平分线MP所在的直线交折线于点P , 设点P在该折线上运动的路径长为 , 连接 .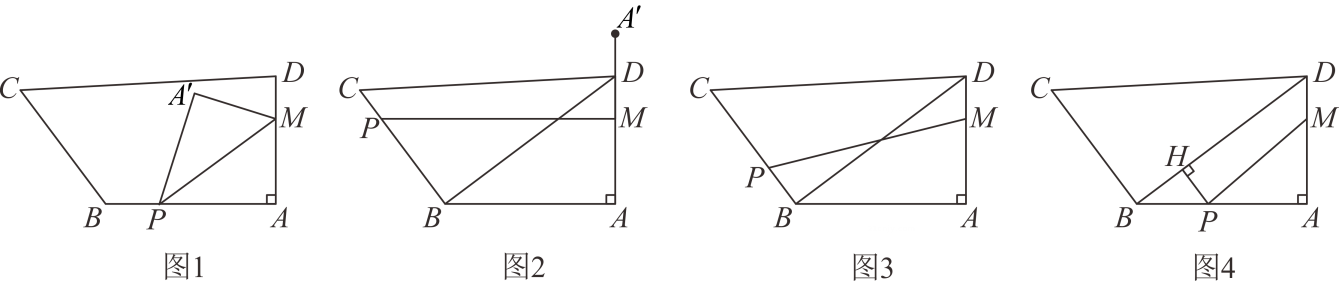 (1)、若点P在AB上,求证:;(2)、如图2,连接BD , 求的度数,并直接写出时,x的值;(3)、如图3和图4,若点P到BD的距离为2,求的值.
(1)、若点P在AB上,求证:;(2)、如图2,连接BD , 求的度数,并直接写出时,x的值;(3)、如图3和图4,若点P到BD的距离为2,求的值.