安徽省合肥市庐江县2023-2024学年九年级上学期期中数学试题（11月）
试卷更新日期：2023-12-04 类型：期中考试
一、选择题（本题共10小题，每小题4分，满分40分）
-
1. 下列函数中，y是x的二次函数的是（ ）A、y= B、y=x2-1 C、y=3x+1 D、y=(x-1)2-x22. 志愿服务，传递爱心，下列志愿服务标志图案为中心对称图形的是（ ）A、
B、
C、
D、
3. 已知x=1是一元二次方程 x2+mx+2=0 的一个解，则m的是（ ）A、-3 B、3 C、0 D、0或34. 用配方法解方程2x2-4x-7=0，下列变形结果正确的是（ ）A、(x-1)2= B、(x-1)2= C、(x-2)2=3 D、(x-1/2)2=75. 若点（0，y1），（1，y2），（3，y3）都在抛物线y=-x2+2x+c上，则y1、y2、y3的大小关系是（ ）A、y2<y1<y3 B、y3<y2<y1 C、y3>y2>y1 D、y3<y1<y26. 如图，将ΔABC绕点C顺时针旋转得到ΔDEC，当点B的对应点E恰好落在边AC上时，连接AD，若∠ACB=30°，则∠DAC的度数是（ ）
A、60° B、65° C、70° D、75°7. 如图，正五边形ABCDE内接于OO，点F是上的动点，则∠AFC的度数为（ ）
A、60° B、72° C、144° D、随着点F的变化而变化8. 定义运算：m☆n=n2-mn-1，例如： 5☆3=32-5×3-1=-7，则方程2☆x=6的根的情况为（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根9. 一次函数 y=kx+k 和二次函数y=-kx2+4x+4（k是常数，且k≠0)在同一平面直角坐标系中的图象可能是（ ）A、
B、
C、
D、
10. 过点P（0，p）的直线与抛物线y=x2交于A，B两点，已知A（a，b）， B(c，a)且a<c，则下列说法正确的是（ ）A、ac>0，若a+c=1，则p有最小值 B、ac>0，若a+c=1，则p有最大值 C、ac<0，若c-a=1，则p有最小值 D、ac<0，若c-a=1，则p有最大值二、填空题（共4小题，每小题5分，满分20分）
-
11. 请写出一个两根分别是1，-2的一元二次方程.（用一般式表示）12. 抛物线y=ax2+bx+c的对称轴是直线x=1，关于x的一元二次方程 ax2+bx+c=0的一个根为x=4，则另一个根为 .13. 如图，在正方形ABCD中，将边BC绕点B逆时针旋转至BC’，连接CC’， DC'，若∠CC'D=90° ， AB=5，则线段C＇D的长度为 .
14. 如图1，E是等边ΔABC的边BC上一点（不与点B，C重合），连接AE，以AE为边向右作等边ΔAEF，连接CF.已知ΔECF的面积S与BE的长x之间的函数关系图象是如图2所示的抛物线，且点P为抛物线的顶点．
(1)、请根据抛物线的对称性，判断当ΔECF的面积最大时，∠FEC=°.(2)、等边ΔABC的边长为 ．三、（本题共2小题，每小题8分，满分16分）
-
15. 解方程：2(x-1)2=18.16. 如图，在平面直角坐标系中，每个小正方形的边长均为1个单位长度，点O和ΔABC的顶点均在小正方形的格点上，请完成下列问题：
⑴画出ΔABC关于点O的中心对称图形ΔA1B1C1；
⑵画出ΔABC绕点B逆时针旋转90°得到的ΔA2BC2 .
四、（本题共2小题，每题8分，满分16分）
-
17. 某公司今年销售一种产品，1月份获得利润20万元，由于产品畅销，利润逐月增加，3月份的利润比2月份的利润增加4.8万元，假设该产品利润每月的增长率相同、求3月份的利润是多少万元？18. 如图是用棋子摆成的图案．根据图中棋子的排列规律解决下列问题：
(1)、第4个图中有颗棋子，第5个图中有颗棋子；(2)、写出你猜想的第n个图中棋子的颗数（用含n的式子表示）是(3)、请求出第几个图形中棋子的个数是274个．五、（本题共2小题，每题10分，满分20分）
-
19. 如图，AB是⊙O 的直径，CD是⊙O的一条弦，且CD⊥AB 于点E．
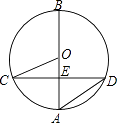(1)、求证：∠BCO=∠D；(2)、若CD=4 ，OE=1，求⊙O的半径．20. 某加工厂要加工一种抛物线型钢材构件，如图所示，该抛物线型构件的底部宽度OM=12米，顶点P到底部OM的距离为9米．将该抛物线放入平面直角坐标系中，点M在x轴上.其内部支架有两个符合要求的设计方案：
方案一：“川”字形内部支架（由线段AB，PN，DC构成），点B，N，C在OM上，且OB=BN=NC=CM，点A，D在抛物线上，AB，PN，DC均垂直于OM；
方案二：“H ”形内部支架（由线段A＇B＇，D＇C＇，EF构成），点B＇，C’在OM上，且OB'=B'C'=C'M，点A＇，D＇在抛物线上，A＇B＇，D＇C＇均垂直于OM，E，F分别是A＇B＇，D＇C＇的中点.
(1)、求该抛物线的函数表达式；(2)、该加工厂要用某一规格的钢材来加工这种构件，那么哪一个方案的内部支架节省材料？请说明理由.六、（本题满分12分）
-
21. 如图1，在ΔABC中，BA=BC，D、E是AC边上的两点，且满足∠DBE=∠ABC ，以点B为旋转中心，将ΔCBE按逆时针方向旋转得到ΔABF，连接DF.
(1)、求证：DF=DE；(2)、如图2，若AB⊥BC，其他条件不变，探究AD，DE，EC之间的关系，并证明.七、（本题满分12分）
-
22. 我们可以用一元二次方程知识研究下面关于“减半”矩形的问题，即：任意给定一个矩形ABCD，是否存在另一个矩形A＇B＇C＇D的周长和面积分别是矩形ABCD周长和面积的一半.(1)、阅读探究过程并完成填空；
当已知矩形ABCD的边长分别是7和1时．
设所求矩形的一边长是x，则另一边长为( - x)，
根据题意，得x( - x)= ，
整理，得2x2-8x+7=0：
∵Δ=64-56=8>0，
∴x1= ； x2= ；
∴满足要求的矩形A＇B＇C＇D＇存在；
(2)、请你继续解决下列问题：①如果已知矩形ABCD的边长分别是2和1，请你仿照上述方法研究是否存在满足要求的矩形A＇B＇C＇D＇；
②如果矩形ABCD的边长为m，n，请你研究满足什么条件时，矩形A＇B＇C＇D＇存在？
八、（本题满分14分）
-
23. 抛物线y=ax2+bx-4(a≠0)与x轴交于点A（-2，0）和B（4，0）．
(1)、求该抛物线的解析式；(2)、若抛物线与y轴交于点C，连接BC．点P是线段BC下方抛物线上的一个动点（不与点B，C重合），过点P作y轴的平行线交BC于M，交x轴于N，设点P的横坐标为t.①求PM的最大值及此时点M的坐标；
②过点C作CH⊥PN于点H，若SΔBMN=9SΔCHM ， 求点P的坐标.
-
-