安徽省皖北片区2023-2024学年九年级上学期期中数学试题

试卷更新日期：2023-12-04 类型：期中考试

进入出卷网下载

一、选择题（共10小题，每题4分，共计40分）

1. 抛物线 $y = - 9 (x - 7)^{2}$ 的顶点坐标是（）

A、 $(9 ， 0)$ B、 $(- 9 ， 7)$ C、 $(9 ， - 7)$ D、 $(7 ， 0)$

查看试题解析
2. 已知 $\frac{a}{b} = \frac{3}{4}$ ，则下列式子中正确的是（）

A、 $a ： b = 9 ： 16$ B、 $a ： b = 6 ： 8$ C、 $a ： b = (a + 3) ： (b + 3)$ D、 $a ： b = 4 ： 3$

查看试题解析
3. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ，直尺的一边与 $B C$ 重合，另一边分别交 $A B$ ， $A C$ 于点 $D$ ， $E .$ 点 $B$ ， $C$ ， $D$ 、 $E$ 处的读数分别为 $15$ ， $12$ ， $0$ ， $1$ ，若直尺宽 $B D = 1 c m$ ，则 $A D$ 的长为（）

A、 $\frac{1}{3} c m$ B、 $\frac{1}{2} c m$ C、 $1 c m$ D、 $\frac{3}{2} c m$

查看试题解析
4. 反比例函数 $y = \frac{6}{x}$ 图象上有三个点 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ， $(x_{3} ， y_{3})$ ，其中 $y_{1} < y_{2} < 0 < y_{3}$ ，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是（）

A、 $x_{1} < x_{2} < x_{3}$ B、 $x_{3} < x_{1} < x_{2}$ C、 $x_{2} < x_{1} < x_{3}$ D、 $x_{3} < x_{2} < x_{1}$

查看试题解析
5. 反比例函数 $y = \frac{k}{x}$ 与二次函数 $y = - k x^{2} + k (k \neq 0)$ 在同一平面直角坐标系中的大致图象是（）

A、 B、 C、 D、

查看试题解析
6. 某班计划在劳动实践基地内种植蔬菜，班长买回来10米长的围栏，准备围成两边靠墙（两墙垂直且足够长）的菜园，为了让菜园面积尽可能大，同学们提出了围成矩形、等腰直角三角形（两直角边靠墙）、扇形这三种方案，如图所示．最佳方案是（）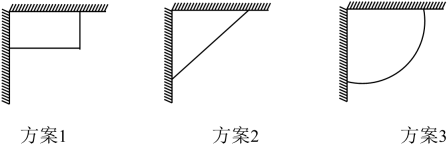

A、方案1 B、方案2 C、方案1或方案2 D、方案3

查看试题解析
7. 如图，在正方形ABCD中，点E在AB边上，AF⊥DE于点G，交BC于点F，若AE=15，BE=5 ，则△AEG的面积与四边形BFGE的面积之比是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{9}{16}$

查看试题解析
8. 如图，在正方形 $A B C D$ 中， $△ B P C$ 是等边三角形， $B P$ 、 $C P$ 的延长线分别交 $A D$ 于点 $E$ ， $F$ ，连接 $B D$ 、 $D P$ ， $B D$ 与 $C F$ 相交于点 $H$ ，给出下列结论：① $∠ D P C = 75 °$ ；② $C F = 2 A E$ ；③ $\frac{D F}{B C} = \frac{2}{3}$ ；④ $△ F P D ∽ △ P H B$ ；⑤ $A F^{2} = E F \cdot E B$ ．其中正确结论的个数是（）

A、5 B、4 C、3 D、2

查看试题解析
9. 已知二次函数 $y = (x - 1) (x - 2)$ ，若关于 $x$ 的方程 $(x - 1) (x - 2) = m (m < 0)$ 的实数根为 $α$ ， $β$ ，且 $α < β$ ，则下列不等式正确的是（）

A、 $α < 1$ ， $β < 2$ B、 $1 < α < β < 2$ C、 $1 < α < 2 < β$ D、 $α < 1 < β < 2$

查看试题解析
10. 如图，在正方形ABCD中，点G是BC上一点，且 $\frac{G C}{B G} = \frac{1}{2}$ ，连接DG交对角线AC于F点，过D点作DE⊥DG交CA的延长线于点E，若AE=3，则DF的长为（）

A、 $2 \sqrt{2}$ B、 $\frac{4 \sqrt{5}}{3}$ C、 $\frac{9}{2}$ D、 $\frac{3 \sqrt{5}}{2}$

查看试题解析

二、填空题（共4小题，每题5分，共计20分）

11. 如图，校园里一片小小的树叶， $P$ 为 $A B$ 的黄金分割点 $(A P > P B)$ ，如果 $A B$ 的长度为 $10 c m$ ，那么 $A P$ 的长度为 $c m$ ．

查看试题解析
12. 从地面竖直向上抛出一小球，小球的高度 $h$ （米）与小球的运动时间（秒）之间的关系式是 $h = 30 t - 5 t^{2} (0 \leq t \leq 6)$ ，若抛出小球1秒钟后再抛出同样的第二个小球．则第二个小球抛出秒时，两个小球在空中的高度相同．

查看试题解析
13. 如图，在函数 $y_{1} = \frac{- 1}{x} (x < 0)$ 和 $y_{2} = \frac{9}{x} (x > 0)$ 的图象上，分别有 $A$ 、 $B$ 两点，若 $A B ∥ x$ 轴，交 $y$ 轴于点 $C$ 且 $O A ⊥ O B$ ，则线段 $A B$ 的长度为．

查看试题解析
14. 如图，在四边形 $A B C D$ 中， $A D = C D = 4$ ， $A B = B C = 3$ ， $D A ⊥ A B$ ， $D C ⊥ B C$ ， $E$ ， $F$ 分别为 $A B$ ， $A D$ 上的点．连结 $C F$ ， $D E$ ， $C F ⊥ D E$ ．

(1)、当点 $E$ 与点 $B$ 重合时， $C F =$ ．

(2)、若点 $E$ 不与点 $A$ ， $B$ 重合，则 $\frac{A F}{B E} =$ ．

查看试题解析

三、解答题（共9小题，15-18每题8分，19-20每题10分，21-22每题12分，23题14分）

15. 已知 $\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = 2$ ，且 $b + d + f \neq 0$ ．

(1)、求 $\frac{a + c + e}{b + d + f}$ 的值；

(2)、若 $b - 2 d + 3 f = 5$ ，求 $a - 2 c + 3 e$ 的值．

查看试题解析
16. 如图，等边三角形△ACB的边长为3，点P为BC上的一点，点D为AC上的一点，连接AP、PD，∠APD=60°．

(1)、求证：△ABP∽△PCD；

(2)、若PC=2，求CD的长．

查看试题解析
17. 如图，在平面直角坐标系中，已知 $△ A B C$ 的三个顶点的坐标分别为 $A (- 4 ， 3)$ ， $B (- 3 ， 1)$ ， $C (- 1 ， 3)$ ，请按下列要求画图：
⑴将 $△ A B C$ 先向右平移4个单位长度、再向下平移5个单位长度，得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ，并写出点 $B_{1}$ 的坐标；
⑵以点 $A$ 为位似中心将 $△ A B C$ 放大2倍，得到 $△ A_{2} B_{2} C_{2}$ ，画出 $△ A_{2} B_{2} C_{2}$ 并写出点 $B_{2}$ 的坐标．

查看试题解析
18. 如图，一次函数 $y_{1} = k x + b (k \neq 0)$ 与函数为 $y_{2} = \frac{m}{x} (x > 0)$ 的图象交于 $A (4 ， 1)$ ， $B (\frac{1}{2} ， a)$ 两点．

(1)、求这两个函数的解析式；

(2)、根据图象，直接写出满足 $y_{1} - y_{2} > 0$ 时 $x$ 的取值范围；

(3)、点 $P$ 在线段 $A B$ 上，过点 $P$ 作 $x$ 轴的垂线，垂足为 $M$ ，交函数 $y_{2}$ 的图象于点 $Q$ ，若 $△ P O Q$ 的面积为3，求点 $P$ 的坐标．

查看试题解析
19. 如图，在足够大的空地上有一段长为40米的旧墙 $M N$ ，某人利用旧墙和木栏围成一个矩形菜园 $A B C D$ ，其中 $A D \leq M N$ ，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．设矩形 $A B C D$ 中，边 $A D$ 为 $x$ 米，面积为 $y$ 平方米．

(1)、求 $y$ 与 $x$ 之间的函数关系式，并写出自变量 $x$ 的取值范围；

(2)、求矩形菜园 $A B C D$ 面积的最大值．

查看试题解析
20. 已知：如图，点 $D$ 、 $E$ 分别在 $△ A B C$ 的边 $A B$ 、 $A C$ 上， $∠ A D E = ∠ B$ ，点 $F$ 在 $A D$ 上，且 $E F ∥ C D$ ．求证：

(1)、 $△ D E F ∽ △ B C D$ ；

(2)、 $A D^{2} = A F \cdot A B$ ．

查看试题解析
21. 如图， $A B ⊥ B D$ ， $C D ⊥ B D$ ， $A B = 6$ ， $C D = 4$ ， $B D = 14$ ，点 $P$ 在 $B D$ 上移动，以 $P$ ， $C$ ， $D$ 为顶点的三角形与 $△ A B P$ 相似时，求 $P B$ 的长．

查看试题解析

22. 某商店销售某种商品的进价为每件30元，这种商品在近60天中的日销售价与日销售量的相关信息如下表：

	时间：第x（天）
	$1 \leq x \leq 30$	$31 \leq x \leq 60$
日销售价（元/件）	$0.5 x + 35$	50
日销售量（件）	$124 - 2 x$

（ $1 \leq x \leq 60$ ， x为整数）

设该商品的日销售利润为w元．

(1)、直接写出w与x的函数关系式；

(2)、该商品在第几天的日销售利润最大？最大日销售利润是多少？

查看试题解析

23. 在四边形 $A B C D$ 中， $∠ A B C = 90 °$ ， $A B = B C$ ，对角线 $A C$ 、 $B D$ 相交于点 $E$ ，过点 $C$ 作 $C F$ 垂直于 $B D$ ，垂足为 $F$ ，且 $C F = D F$ ．
图1 图2

(1)、求证： $△ A C D ∽ △ B C F$ ；

(2)、如图2，连接 $A F$ ，点 $P$ 、 $M$ 、 $N$ 分别为线段 $A B$ 、 $A F$ 、 $D F$ 的中点，连接 $P M$ 、 $M N$ 、 $P N$ ．
①求证： $∠ P M N = 135 °$ ；
②若 $A D = 2 \sqrt{2}$ ，求 $△ P M N$ 的面积．

查看试题解析