安徽省芜湖市2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-04 类型:期中考试
一、选择题:每小题给出的四个选项中,其中只有一个是正确的。请把正确选项的代号写在下面的答题表内(本大题共10小题,每题4分,共40分)
-
1. 将一元二次方程化成一般形式后,它的二次项系数是2,则一次项系数是( ).A、 B、3 C、 D、12. 一元二次方程有一根是 , 则另一根是( )A、 B、 C、 D、3. 点关于原点对称的点的坐标为( ).A、 B、 C、 D、4. 方程根的情况是( ).A、有两个不相等的实数根 B、有两个相等的实数根 C、有一个实数根 D、没有实数根5. 将抛物线向上平移6个单位,再向右平移9个单位,得到的抛物线的解析式为( ).A、 B、 C、 D、6. 2023年杭州第19届亚运会羽毛球比赛共产生7枚金牌,比赛中某次羽毛球的运动路线可以看作是如图所示的抛物线图象的一部分,其中出球点离地面点的距离是1米,则球落地点到点的距离是( ).
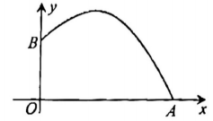 A、1米 B、3米 C、4米 D、米7. 如图,在中, , 将绕点逆时针旋转角度()得到 , 若 , 则的值为( )
A、1米 B、3米 C、4米 D、米7. 如图,在中, , 将绕点逆时针旋转角度()得到 , 若 , 则的值为( ) A、 B、 C、 D、8. 二次函数 与一次函数 的图象交于点 和点 ,要使 ,则x的取值范围是( )A、 B、 C、 D、 或9. 已知函数 , 下列结论错误的是( ).A、当时,随的增大而增大 B、当时,函数图象的顶点坐标是 C、当时,若 , 则随的增大而减小 D、无论取何值,函数图象不经过同一个点10. 如图,点是等边三角形边的中点,点是直线上一动点,连接 , 并绕点逆时针旋转 , 得到线段 , 连接 . 若运动过程中的最小值为 , 则长为( ).
A、 B、 C、 D、8. 二次函数 与一次函数 的图象交于点 和点 ,要使 ,则x的取值范围是( )A、 B、 C、 D、 或9. 已知函数 , 下列结论错误的是( ).A、当时,随的增大而增大 B、当时,函数图象的顶点坐标是 C、当时,若 , 则随的增大而减小 D、无论取何值,函数图象不经过同一个点10. 如图,点是等边三角形边的中点,点是直线上一动点,连接 , 并绕点逆时针旋转 , 得到线段 , 连接 . 若运动过程中的最小值为 , 则长为( ).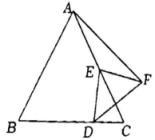 A、2 B、 C、 D、4
A、2 B、 C、 D、4二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 如图,在中, , 点在上,且 , 将点绕着点顺时针方向旋转,使得点的对应点恰好落在边上,则的长为 .
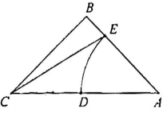 12. 如图,抛物线交轴的负半轴于点 , 点是轴的正半轴上一点,点关于点的对称点恰好落在抛物线上.过点作轴的平行线交抛物线于另一点 , 则点的坐标为 .
12. 如图,抛物线交轴的负半轴于点 , 点是轴的正半轴上一点,点关于点的对称点恰好落在抛物线上.过点作轴的平行线交抛物线于另一点 , 则点的坐标为 . 13. 若实数满足 , 则的值是 .14. 已知抛物线 , 经过点 .(1)、若时, , 则此抛物线的对称轴为;(2)、当且时,都有 , 则的取值范围为 .
13. 若实数满足 , 则的值是 .14. 已知抛物线 , 经过点 .(1)、若时, , 则此抛物线的对称轴为;(2)、当且时,都有 , 则的取值范围为 .三、(本大题共2小题,每小题8分,满分16分)
-
15. 解方程: .16. 如图,在正方形网格中,每个小正方形的边长为1,格点(顶点在网格线的交点上)的顶点的坐标分别为
 (1)、在网格所在的平面内,请画出平面直角坐标系;(2)、将绕着原点顺时针旋转得 , 画出 .
(1)、在网格所在的平面内,请画出平面直角坐标系;(2)、将绕着原点顺时针旋转得 , 画出 .四、(本大题共2小题,每小题8分,满分16分)
-
17. “呵护一抹绿色,成就城市清新”.某市为改善城市容貌,绿化环境,计划经过两年时间,使绿地面积增加 , 求该市这两年平均每年绿地面积的增长率.18. 如图,下列图形是由边长为1个单位长度的小正方形按照一定规律摆放的“”形图形,观察图形:
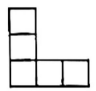

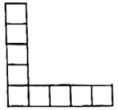
图1 图2 图3
(1)、按此规律,图4中小正方形的数量是个;(2)、我们把图1中小正方形个数记作 , 图2中小正方形图个数记作 , 图中小正方形个数记作 , 若 , 求的值.五、(本大题共2小题,每小题10分,满分20分)
-
19. 已知函数的图象与轴有交点,求的取值范围.20. 已知二次函数的图象顶点为 .
 (1)、请直接写出点的坐标;(2)、请通过列表描点,画出该二次函数的大致图象;(3)、当时,则的取值范围是 . (直接写出结果)
(1)、请直接写出点的坐标;(2)、请通过列表描点,画出该二次函数的大致图象;(3)、当时,则的取值范围是 . (直接写出结果)六、(本题满分12分)
-
21. 某商场将进货价为45元的某种服装以65元售出,平均每天可售30件.为了尽快减少库存,商场决定采取适当的降价措施,调查发现:每件降价1元,则每天可多售5件.如果每天要盈利800元,每件应降价多少元.
七、(本题满分12分)