四川省眉山市仁寿县2023-2024学年八年级上学期数学期中考试试卷

试卷更新日期：2023-12-04 类型：期中考试

进入出卷网下载

一、选择题：（每小题4分，共12小题，共计48分）

1. 下列计算正确的是（）

A、 $\sqrt{(- 3)^{2}} = - 3$ B、 $\sqrt{36} = \pm 6$ C、 $\sqrt[3]{9} = 3$ D、 $- \sqrt[3]{- 8} = 2$

查看试题解析
2. 下列运算正确的是（）

A、 $a_{}^{2} \cdot a_{}^{3} = a_{}^{5}$ B、 $a + 2 a = 3 a_{}^{2}$ C、 $(a b)_{}^{3} = a b_{}^{3}$ D、 $(- a_{}^{3})_{}^{2} = - a_{}^{6}$

查看试题解析
3. 下面式子从左边到右边的变形是因式分解的是（）

A、 $x_{}^{2} - 4 y_{}^{2} = (x + y) (x - 4 y)$ B、 $(x + 4) (x - 4) = x_{}^{2} - 16$ C、 $x_{}^{2} - 2 x + 1 = (x - 1)_{}^{2}$ D、 $x_{}^{2} - 8 x + 9 = (x - 4)_{}^{2} - 7$

查看试题解析
4. 计算 $(- \frac{2}{3})_{}^{2023} \times (\frac{3}{2})_{}^{2022}$ 的结果是（）

A、 $- \frac{3}{2}$ B、 $- \frac{2}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{2}$

查看试题解析
5. 一个三角形的面积为（x³y）² ，它的一条边长为（2xy）² ，那么这条边上的高为（　　）

A、 $\frac{1}{2} x^{4}$ B、 $\frac{1}{4} x^{4}$ C、 $\frac{1}{2} x^{4} y$ D、 $\frac{1}{2} x^{2}$

查看试题解析
6. 下列命题真命题的个数有（）
①过一点有且只有一条直线与已知直线平行；
②直线外一点与直线上各点连接的所有线段中，垂线段最短；
③若 $a > b$ ，则 $c - a > c - b$ ；
④无理数都是无限小数；
⑤平方根等于本身的数是 $0$ 和 $1$ ．

A、 $4$ 个 B、 $3$ 个 C、 $2$ 个 D、 $1$ 个

查看试题解析
7. 已知实数 $a$ ， $b$ 在数轴上的对应点如图，则化简 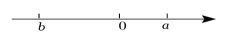$\sqrt{(a + b)_{}^{2}} - \sqrt{(a - b)_{}^{2}} - \sqrt{a_{}^{2}}$ 得（）

A、 $- 3 a$ B、 $- a + 2 b$ C、 $- 2 a$ D、 $a - b$

查看试题解析
8. 如图，大正方形与小正方形的面积之差是50，则阴影部分的面积是（）

A、12.5 B、25 C、50 D、100

查看试题解析
9. 多项式 $x^{2} + x - 6$ 可因式分解成 $(x + a) (x + b)$ ，其中 $a$ ， $b$ 均为整数，则 ${(a + b)}^{2023}$ 的值为（）

A、 $- 1$ B、1 C、 $- 2023$ D、2023

查看试题解析
10. 设 $a$ ， $b$ 是实数，定义一种新运算： $a * b = (a - b)_{}^{2}$ ．下面有四个推断：① $a * b = b * a$ ， ② $(a * b)_{}^{2} = a_{}^{2} * b_{}^{2}$ ， ③ $a * (b - c) = (b - c) * a$ ， ④ $a * (b + c) = a * b + a * c$ ，其中所有正确推断的序号是（）

A、①②③④ B、①③④ C、①③ D、①②

查看试题解析
11. 对于五个整式， $A$ ： $2 x_{}^{2}$ ； $B$ ： $x + 1$ ； $C$ ： $- 2 x$ ； $D$ ： $y_{}^{2}$ ； $E$ ： $2 x - y$ 有以下几个结论：①若 $y$ 为正整数，则多项式 $B \cdot C + A + D + E$ 的值一定是正数；
②存在有理数 $x$ ， $y$ ，使得 $A + D + 2 E$ 的值为 $- 2$ ；
③若关于 $x$ 的多项式 $M = 3 (A - B) + m B \cdot C$ （ $m$ 为常数）不含 $x$ 的一次项，则该多项式 $M$ 的值一定大于 $- 3$ ．上述结论中，正确的个数是（）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看试题解析
12. 已知 $a_{}^{2} + b_{}^{2} = 9$ ，则ab-b+a的最大值为（）

A、3 B、5 C、 $\frac{9}{2}$ D、 $\frac{25}{4}$

查看试题解析

二、填空题（每题4分，共6题，共计24分）

13. 若a^x=2，a^y=3，则a^x+y=.

查看试题解析
14. 已知 $a + 1$ 的平方根是 $\pm 2$ ， $2 a + b - 2$ 的立方根是 $2$ ，则 $a_{}^{2} + b_{}^{2}$ 的算术平方根是

查看试题解析
15. 当 $4 x_{}^{2} + 2 k x + 25$ 是一个完全平方式，则 $k$ 的值是

查看试题解析
16. 若 $m - n = 4$ ， $m n = - 3$ ，则 $(m_{}^{2} - 4) (n_{}^{2} - 4)$ 的值等于

查看试题解析
17. 若 $\sqrt{a^{2} - 3 a + 1} + b^{2} + 2 b + 1 = 0$ ，则 $a^{2} + \frac{1}{a^{2}} - | b |$ =.

查看试题解析
18. 已知 $a = \sqrt{17} - 1$ ，则 $a_{}^{5} + 2 a_{}^{4} - 17 a_{}^{3} - a_{}^{2} + 18 a - 17$ 的值等于

查看试题解析

三、解答题：（共8题，共计78分）

19. 计算：

(1)、 $(\sqrt{2})_{}^{2} - | 1 - \sqrt{3} | + \sqrt{(- 3)_{}^{2}} + \sqrt{81}$

(2)、 $(x - 2 y)_{}^{2} - (x + 2 y + 3) (x + 2 y - 3)$

查看试题解析
20. 因式分解：

(1)、 $- 10 x y_{}^{2} + y_{}^{3} + 25 x_{}^{2} y$

(2)、 $a_{}^{3} + a_{}^{2} b - a b_{}^{2} - b_{}^{3}$

查看试题解析
21. 已知 $x$ ， $y$ 满足 $(x - 2)_{}^{2} + | y - 3 | = 0$ ．
先化简，再求值： $[(x - 2 y) (x + 2 y) - (x - y)_{}^{2} + y (y + 2 x)] \div (- 2 y)$ ．

查看试题解析
22. 【材料】： $∵$ $\sqrt{4} < \sqrt{6} < \sqrt{9}$
∴ $2 < \sqrt{6} < 3$
∴ $\sqrt{6}$ 的整数部分是 $2$ ，小数部分是 $\sqrt{6} - 2$ ．

(1)、【应用】：
$\sqrt{30}$ 的整数部分是，小数部分是．

(2)、已知 $6 + \sqrt{15}$ 的整数部分是 $x$ ， $6 - \sqrt{15}$ 的小数部分是 $y$ ，求 $x + y$ 的值．

(3)、【拓展】：已知 $a$ ， $b$ 为有理数，且 $(a + \sqrt{3})_{}^{2} = b - 8 \sqrt{3}$ ，求 $a - b$ 的值.

查看试题解析
23. 若 $(x_{}^{2} + a x - \frac{1}{3}) (x_{}^{2} - 3 x + b)$ 的积中不含 $x$ 项与 $x_{}^{3}$ 项，

(1)、求 $a$ 、 $b$ 的值；

(2)、求代数式 $(- 2 a_{}^{2} b)_{}^{2} + 3 a b$ 的值.

查看试题解析
24. 如图，学校操场主席台前计划修建一块凹字形花坛．（单位：米）

(1)、用含 $a$ ， $b$ 的整式表示花坛的面积；

(2)、若 $a = 2$ ， $b = 1$ ，工程费为 $500$ 元/平方米，求建花坛的总工程费为多少元?

查看试题解析
25. 我们知道，分解因式与整式乘法是互逆的运算.在分解因式的练习中我们也会遇到下面的问题，请你根据情况解答：

(1)、已知 $a$ ， $b$ ， $c$ 是 $Δ A B C$ 的三边，且满足 $a_{}^{2} + 2 b_{}^{2} = 2 b (a + c) - c_{}^{2}$ .
判断 $Δ A B C$ 的形状；

(2)、两位同学将一个二次三项式 $a x_{}^{2} + b x + c$ 分解因式时，其中一位同学因看错了一次项系数而分解成 $3 (x - 1) (x + 2)$ ，另一位同学因看错了常数项而分解成 $3 (x + 2) (x - 3)$ ，请你求出原来的多项式并将原式分解因式.

查看试题解析
26. 【知识生成】我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式．例如图 $1$ 可以得到 $(a + b)_{}^{2} = a_{}^{2} + 2 a b + b_{}^{2}$ ，基于此，请解答下列问题：

(1)、【直接应用】若 $x + y = 3$ ， $x_{}^{2} + y_{}^{2} = 5$ ，求 $x y$ 的值；

(2)、【类比应用】①若 $(x - 3) (x - 4) = 1$ ，则 $(x - 3)_{}^{2} + (x - 4)_{}^{2}$ = ；
②若 $x$ 满足 $(3 - 4 x) (2 x - 5) = \frac{9}{2}$ ，求 $(3 - 4 x)_{}^{2} + 4 (2 x - 5)_{}^{2}$ 的值；
③若 $x$ 满足 $(2023 - x)^{2} + (2020 - x)^{2} = 2023$ ，求 $(2023 - x) (2020 - x)$ 的值；

(3)、【知识迁移】两块全等的特制直角三角板（ $∠ A O B = ∠ C O D = 90 °$ ）如图 $2$ 所示放置，其中 $A$ ， $O$ ， $D$ 在一直线上，连接 $A C$ ， $B D$ ．若 $A D = 16$ ， $S_{Δ A O C}^{} + S_{Δ B O D}^{} = 68$ ，求一块直角三角板的面积．

查看试题解析