备考2024年高考数学二轮复习1 统计概率、分布列的综合应用的突破训练
试卷更新日期:2023-12-04 类型:二轮复习
一、解答题
-
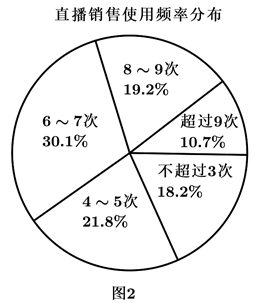
1. 直播带货是扶贫助农的一种新模式,这种模式是利用主流媒体的公信力,聚合销售主播的力量助力打通农产品产销链条,切实助力贫困地区农民脱贫增收.某贫困地区有统计数据显示,2020年该地利用网络直播形式销售农产品的销售主播年龄等级分布如图1所示,一周内使用直播销售的频率分布扇形图如图2所示.若将销售主播按照年龄分为“年轻人”(20岁~39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的称为“经常使用直播销售用户”,使用次数为5次或不足5次的称为“不常使用直播销售用户”,则“经常使用直播销售用户”中有 是“年轻人”.

参考数据:独立性检验临界值表
0.15
0.10
0.050
0.025
0.010
2.072
2.706
30841
5.024
6.635
其中, .
(1)、现对该地相关居民进行“经常使用网络直播销售与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,完成 列联表,并根据列联表判断是否有85%的把握认为经常使用网络直播销售与年龄有关?使用直播销售情况与年龄列联表
年轻人
非年轻人
合计
经常使用直播销售用户
不常使用直播销售用户
合计
(2)、某投资公司在2021年年初准备将1000万元投资到“销售该地区农产品”的项目上,现有两种销售方案供选择:方案一:线下销售.根据市场调研,利用传统的线下销售,到年底可能获利30%,可能亏损15%,也可能不赔不赚,且这三种情况发生的概率分别为 ;
方案二:线上直播销售.根据市场调研,利用线上直播销售,到年底可能获利50%,可能亏损30%,也可能不赔不赚,且这三种情况发生的概率分别为 .
针对以上两种销售方案,请你从期望和方差的角度为投资公司选择一个合理的方案,并说明理由.
2. 篮球职业联赛通常分为常规赛和季后赛两个阶段.常规赛采用循环赛,胜率高或者积分高的球队进入季后赛,季后赛是淘汰赛,采用三局两胜制进行淘汰,最终决出总冠军.三局两胜制是指当比赛一方先赢得两局比赛时该方获胜,比赛结束.附:
0.100
0.050
0.010
2.706
3.841
6.635
(1)、下表是甲队在常规赛80场比赛中的比赛结果记录表,由表中信息,依据的独立性检验,分析“主场”是否会增加胜率(计算结果保留两位小数).月份
比赛次数
主场次数
获胜次数
主场获胜次数
10月
8
3
6
3
11月
15
10
8
8
12月
14
7
8
5
1月
13
4
11
3
2月
11
7
6
5
3月
14
6
7
3
4月
5
3
4
3
(2)、甲队和乙队在季后赛中相遇,经过统计甲队在主场获胜的概率为 , 客场获胜的概率为.每场比赛场地为上一场比赛的获胜方的场地.(i)若第一场比赛在甲队的主场进行,设整个比赛的进行的局数为 , 求的分布列及数学期望;
(ii)设选择第一场为甲队的主场的概率为 , 问当为何值时,无论第一场比赛的场地在哪里,甲队最终获胜的概率相同,并求出此时甲队获胜的概率.
3. 如图,是一块高尔顿板的示意图,在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入编号为的球槽内.用X表示小球经过第7层通过的空隙编号(从左向右的空隙编号依次为),用Y表示小球最后落入球槽的号码.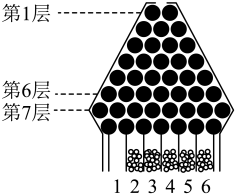 (1)、若进行一次高尔顿板试验,求小球落入第7层第3个空隙处的概率;(2)、若放入80个小球,求落入1号球槽的小球个数Z的均值与方差.4. 某同学进行投篮训练,已知该同学每次投中的概率均为0.5.
(1)、若进行一次高尔顿板试验,求小球落入第7层第3个空隙处的概率;(2)、若放入80个小球,求落入1号球槽的小球个数Z的均值与方差.4. 某同学进行投篮训练,已知该同学每次投中的概率均为0.5.附:若表示投篮的次数,表示投中的次数,则投中的频率为;若 , 则.
(1)、若该同学进行三次投篮,第一次投中得1分,第二次投中得1分,第三次投中得2分,记为三次总得分,求的分布列及数学期望;(2)、已知当随机变量服从二项分布时,若充分大,则随机变量服从标准正态分布.若保证投中的频率在0.4与0.6之间的概率不低于 , 求该同学至少要投多少次.5. 为迎接“五一小长假”的到来,某商场开展一项促销活动,凡在商场消费金额满200元的顾客可以免费抽奖一次,抽奖规则如下:在不透明箱子中装有除颜色外其他都相同的10个小球,其中,红球2个,白球3个,黄球5个,顾客从箱子中依次不放回地摸出2个球,根据摸出球的颜色情况分别进行兑奖.将顾客摸出的2个球的颜色分成以下四种情况::1个红球1个白球,:2个红球,:2个白球,:至少一个黄球.若四种情况按发生的概率从小到大的顺序分别对应一等奖,二等奖,三等奖,不中奖.(1)、求顾客在某次抽奖中,第二个球摸到为红球的概率(2)、求顾客分别获一、二、三等奖时对应的概率;(3)、若三名顾客每人抽奖一次,且彼此是否中奖相互独立.记中奖的人数为 , 求的分布列和期望.6. 某手机APP公司对喜欢使用该APP的用户年龄情况进行调查,随机抽取了100名喜欢使用该APP的用户,年龄均在周岁内,按照年龄分组得到如下所示的样本频率分布直方图: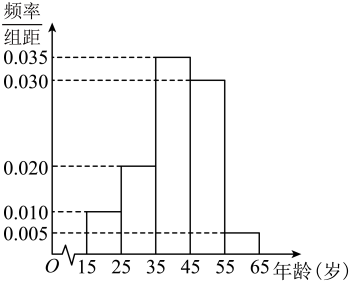
附:若随机变量服从正态分布 , 则:
(1)、根据频率分布直方图,估计使用该视频APP用户的平均年龄的第分位数(小数点后保留2位);(2)、若所有用户年龄近似服从正态分布 , 其中为样本平均数的估计值, , 试估计喜欢使用该APP且年龄大于61周岁的人数占所有喜欢使用该APP的比例;(3)、用样本的频率估计概率,从所有喜欢使用该APP的用户中随机抽取8名用户,用表示这8名用户中恰有名用户的年龄在区间岁的概率,求取最大值时对应的的值;7. 羽毛球运动具有拼搏、进步、积极向上的意义,同时还要求运动员具备细心和迅速的敏锐性.某大学羽毛球运动协会为了了解本校学生对羽毛球运动是否有兴趣,从该校学生中随机抽取了300人进行调查,男女人数之比是2:1,其中女生对羽毛球运动有兴趣的占80%,而男生有30人表示对羽毛球运动没有兴趣.附表: , 其中.
a
0.50
0.40
0.25
0.150
0.100
0.050
0.455
0.780
1.323
2.072
2.706
3.841
(1)、完成2×2列联表,根据小概率值的独立性检验,能否认为“对羽毛球运动是否有兴趣与性别有关”?有兴趣
没兴趣
合计
男
女
合计
(2)、为了提高同学们对羽毛球运动的参与度,该校举行一次羽毛球比赛.比赛分两个阶段进行,第一阶段的比赛赛制采取单循环方式,每场比赛采取三局二胜制,然后由积分的多少选出进入第二阶段比赛的同学,每场积分规则如下:比赛中以2:0取胜的同学积3分,负的同学积0分;以2:1取胜的同学积2分,负的同学积1分.其中,小强同学和小明同学的比赛倍受关注,设每局小强同学取胜的概率为 , 记小强同学所得积分为X,求X的分布列和期望.8. 甲、乙两名围棋学员进行围棋比赛,规定每局比赛胜者得1分,负者得0分,平局双方均得0分,比赛一直进行到一方比另一方多两分为止,多得两分的一方赢得比赛.已知每局比赛中,甲获胜的概率为α,乙获胜的概率为β,两人平局的概率为 , 且每局比赛结果相互独立.(1)、若 , , , 求进行4局比赛后甲学员赢得比赛的概率;(2)、当时,(i)若比赛最多进行5局,求比赛结束时比赛局数X的分布列及期望E(X)的最大值;
(ii)若比赛不限制局数,写出“甲学员赢得比赛”的概率(用α,β表示),无需写出过程.
9. 某服装公司经过多年发展,在全国布局了3500余家规模相当的销售门店.该公司每年都会设计生产春季新款服装并投放到全国各个门店销售.公司为了了解2022年春季新款服装在各个销售门店的销售情况,市场部随机调查了20个销售门店的年销售额(单位:万元,不考虑门店之间的其它差异),统计结果如下:门店编号
1
2
3
4
5
6
7
8
9
10
销售额
45
33
30
44
28
22
37
21
19
24
门店编号
11
12
13
14
15
16
17
18
19
20
销售额
34
41
23
20
37
31
29
32
36
42
(1)、从以上20个门店中随机抽取3个,求抽取的3个门店中至少有2个的年销售额超过40万元的概率;(2)、以样本频率估计概率,现从全国销售门店中随机抽取3个,记该年春季新款的年销售额超过40万元的销售门店的个数为 , 求的分布列及数学期望.10. 天宫空间站是我国建成的国家级太空实验室,由天和核心舱、问天实验舱和梦天实验舱组成,已经开启长期有人驻留模式,结合空间站的相关知识,某职业学校的老师设计了以空间站为主题的编程训练,训练内容由“太空发射”、“自定义漫游”、“全尺寸太阳能”、“空间运输”等10个相互独立的编程题目组成,训练要求每个学生必须选择两个不同的题目进行编程练习,并且学生间的选择互不影响,老师将班级学生分成四组,指定甲、乙、丙、丁为组长.(1)、求甲、乙、丙、丁这四个人中至少有一人选择“太空发射”的概率;(2)、记X为这四个人中选择“太空发射”的人数,求X的分布列及数学期望;(3)、如果班级有n个学生参与编程训练(其中n是能被5整除的正整数),则这n个学生中选择“太空发射”的人数最有可能是多少人?11. 某市为了传承发展中华优秀传统文化,组织该市中学生进行了一次文化知识有奖竞赛,竞赛奖励规则如下:得分在内的学生获三等奖,得分在内的学生获二等奖,得分在内的学生获一等奖,其他学生不得奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了如图所示的样本频率分布直方图.
附:若随机变量服从正态分布 , 则 , , .
(1)、现从该样本中随机抽取2名学生的竞赛成绩,求这2名学生中恰有1名学生获奖的概率;(2)、估计这100名学生的竞赛成绩的平均数(同一组中的数据用该组区间的中点值作代表);(3)、若该市共有10000名学生参加了竞赛,所有参赛学生的成绩近似服从正态分布 , 其中 , 为样本平均数的估计值,试估计参赛学生中成绩超过78分的学生人数(结果四舍五入到整数).12. 随着春季学期开学,某市市场监管局加强了对学校食堂食品安全管理,助力推广校园文明餐桌行动,培养广大师生文明餐桌新理念,以“小餐桌”带动“大文明”,同时践行绿色发展理念.该市某中学有A,B两个餐厅为老师与学生们提供午餐与晚餐服务,王同学、张老师两人每天午餐和晚餐都在学校就餐,近一个月(30天)选择餐厅就餐情况统计如下:选择餐厅情况(午餐,晚餐)
王同学
9天
6天
12天
3天
张老师
6天
6天
6天
12天
假设王同学、张老师选择餐厅相互独立,用频率估计概率.
(1)、估计一天中王同学午餐和晚餐选择不同餐厅就餐的概率;(2)、记X为王同学、张老师在一天中就餐餐厅的个数,求X的分布列和数学期望;(3)、假设M表示事件“A餐厅推出优惠套餐”,N表示事件“某学生去A餐厅就餐”, , 已知推出优惠套餐的情况下学生去该餐厅就餐的概率会比不推出优惠套餐的情况下去该餐厅就餐的概率要大,证明: .13. 2022年10月16日至10月22日,中国共产党第二十次全国代表大会在北京召开,此次大会是在全党全国各族人民迈上全面建设社会主义现代化国家新征程、向第二个百年奋斗目标进军的关键时刻召开的一次十分重要的大会.在树人中学团委的组织下,高二年级各班团支部举行了“学习二十大,做有为青年”的知识竞赛活动,经过激烈竞争,高二(1)班(以下简称一班)和高二(3)班(以下简称三班)进入了最后的年级决赛,决赛规定:共进行5轮比赛,每轮比赛每个班可以从A,B两个题库中任选1题作答,在前两轮比赛中每个班的题目必须来自同一题库,后三轮比赛中每个班的题目必须来自同一题库,A题库每题20分,B题库每题30分,一班能正确回答A、B题库每题的概率分别为、 , 三班能正确回答A、B题库每题的概率均为 , 且每轮答题结果互不影响.(1)、若一班前两轮选A题库,后三轮选B题库,求其总分不少于100分的概率;(2)、若一班和三班在前两轮比赛中均选了B题库,而且一班两轮得分60分,三班两轮得分30分,一班后三轮换成A题库,三班后三轮不更换题库,设一班最后的总分为X,求X的分布列,并从每班总分的均值来判断,哪个班赢下这场比赛?