浙江省丽水市龙泉市2023-2024学年九年级第一学期数学期中考试试卷

试卷更新日期：2023-12-01 类型：期中考试

进入出卷网下载

一、选择题(本题有10小题,每小题3分,共30分)

1. 下列函数是二次函数的是（）

A、y＝2x＋1 B、y＝－2x＋1 C、y＝ $\frac{1}{2}$ x－2 D、y＝x²＋2

查看试题解析
2. 下列事件中，随机事件是（）

A、6-5=1 B、打开电视机正在播报新闻 C、水中捞月 D、太阳从西边升起

查看试题解析
3. 任意抛掷一枚硬币，出现正面朝上的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、1

查看试题解析
4. 二次函数y＝(x－2)²－3的顶点坐标是（）

A、(－2，－3) B、(－2，3) C、(2，3) D、(2，－3)

查看试题解析
5. 如图，已知A，B均为⊙O上一点，若∠AOB＝80°，则∠ACB＝（）

A、40° B、80° C、60° D、70°

查看试题解析
6. 二次函数y＝ax²(a≠0)的图象经过点(1，2)，则a的值是（）

A、 B、 C、2 D、4

查看试题解析
7. 如图，AB为⊙O的直径，C，D为⊙O上两点，若∠CAB＝35°，则∠D＝（）

A、35° B、55° C、65° D、70°

查看试题解析
8. 设A(－5，y₁)，B(1，y₂)，C(2，y₃)是抛物线y＝－(x＋1)²＋3上的三点，则y₁ ， y₂ ， y₃的大小关系为（）

A、y₂＞y₃＞y₁ B、y₁＞y₃＞y₂ C、y₃＞y₂＞y₁ D、y₃＞y₁＞y₂

查看试题解析
9. 如图，⊙O的半径是3，点P是弦AB延长线上的一点，连结OP，若OP＝4，∠APO＝30°，则弦AB的长为（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、2 $\sqrt{3}$ D、2 $\sqrt{5}$

查看试题解析
10. 若b≤x≤b＋3时，二次函数y＝x²＋bx＋b²的最小值为15，则b的值为（）

A、-或 $\frac{- 3 + \sqrt{17}}{2}$ B、或 $\frac{- 3 - \sqrt{17}}{2}$ C、2或 $\frac{- 3 + \sqrt{17}}{2}$ D、-2或

查看试题解析

二、填空题(本题有6小题,每小题4分,共24分)

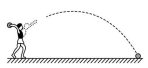
11. 20瓶饮料有3瓶已过保质期，从20瓶饮料中任取1瓶，取到已过保质期的饮料的概率是.

查看试题解析
12. 已知⊙O的半径为5，点P在⊙O上，则OP的长为.

查看试题解析
13. 将抛物线y＝－x²向上平移2个单位，得到抛物线的解析式是.

查看试题解析
14. 正五边形的一个外角的度数是°.

查看试题解析
15. 在中考体育训练期间，小宇对自己某次实心球训练的录像进行分析，发现实心球飞行高度y（米）与水平距离x（米）之间的关系式为y=- $\frac{1}{10}$ x²+ $\frac{3}{5}$ x+ $\frac{8}{5}$ ，由此可知小宇此次实心球训练的成绩为米.

查看试题解析
16. 如图，AB是半圆O的直径，点C在半圆O上，AB＝4，∠CAB＝60°，P是弧BC上的一个动点，连结AP，过点C点作CD⊥AP于点D，连结BD，在点P移动的过程中.

(1)、AC＝；

(2)、BD的最小值是.

查看试题解析

三、解答题(本题有8小题,第17～19题每题6分,第20,21题每题8分,第22,23题每题10分,第24题12分,共66分,各小题都必须写出解答过程)

17. 已知二次函数y＝x²＋bx＋c经过点A(0，3)，点B(1，2).

(1)、求b，c的值；

(2)、求该二次函数的对称轴.

查看试题解析
18. 一个布袋里装有3个只有颜色不同的球，其中2个红球，1个白球.

(1)、摸出一个球是红球的概率；

(2)、从布袋里摸出1个球，记下颜色后放回，搅匀，再摸出1个球.求两次都摸到红球的概率.

查看试题解析
19. 已知：如图，在△ABC中，AB=AC，以边AB为直径作半圆O，分别交BC，AC于点D，E.

(1)、求证：BD＝DC；

(2)、若∠BAC＝40°，求弧DE的度数.

查看试题解析
20. 请按要求作图，并保留作图痕迹.

(1)、如图1，AB是圆的一条弦，用直尺（无刻度）和圆规在图中作圆的一条直径；

(2)、如图2，正五边形ABCDE内接于圆，仅用直尺（无刻度）作出一条直径.

查看试题解析

21.

测算石拱桥拱圈的半径
素材1	在日常生活中，如果没有带测量工具，那么我们可以用身体的“尺子”来测量，比如前臂长(包括手掌、手指)称为1肘(如图1)，现利用该方法测得一块矩形花岗岩的长和高(如图2)．
素材2	某数学兴趣小组测算一座石拱桥拱圈的半径(如图3)，石拱桥由以上矩形的花岗岩叠砌而成，上、下的花岗岩错缝连结(花岗岩的各个顶点落在上、下花岗各边的中点，如图3所示).
素材3	通过观察发现A，B两个点都在拱圈上.A是拱圈的最高点，且在两块花岗岩连结顶点处，B是花岗岩的顶点(如图4).
问题解决
任务1	获取数据	通过观察、计算A，B两点之间的水平距离及铅垂距离(高度差).
任务2	分析计算	通过观察、计算石拱桥拱圈的半径.

注：测量、计算时，都以“肘”为单位.

查看试题解析

22. 某书店销售儿童期刊，一天可售出20套，每套盈利30元.为了扩大销售，增加盈利，尽快减少库存，书店决定采取降价措施.若一套书每降价1元，平均每天可多售出2套.设每套书降价x元时，书店一天可获利润y元.

(1)、求y关于x的函数表达式；

(2)、若书店每天要盈利750元，则需降价多少元？

(3)、当每套书降价多少元时，书店可获最大利润？最大利润是多少？

查看试题解析
23. 已知关于x的二次函数y＝ax²－2ax＋3a－2(a≠0)，经过点A(x₁ ， y₁)，B(x₂ ， y₂).

(1)、若此函数图象过点(2，4)，求这个二次函数的表达式；

(2)、若x₁＝3x₂时，y₁＝y₂＝7时，求x₂的值；

(3)、若0＜a＜3，当x₁＜x₂ ，且x₁＋x₂＝a－1时，求证：y₁＞y₂.

查看试题解析
24. 如图，AB是⊙O的直径，AB＝4，点E为弧AC的中点，连结AC，BE交于点D，过点A作AF⊥AB交BE的延长线于点F，AF＝3.

(1)、求证：AD=AF；

(2)、求△ABD的周长；

(3)、若点P为⊙O上一点，当△AEP为等腰三角形时，求AP的长.

查看试题解析