浙江省丽水市龙泉市2023-2024学年八年级第一学期数学期中考试试卷
试卷更新日期：2023-12-01 类型：期中考试
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 下列标志中，属于轴对称图形的是（ ）A、
B、
C、
D、
2. 下列各组线段能组成三角形的是（ ）A、1，2，3 B、5，5，11 C、5，6，11 D、6，8，133. 如图所示，在数轴上表示不等式正确的是（ ）
A、 B、 C、 D、4. 下列能说明命题“任何偶数都是4的倍数”是假命题的反例是（ ）A、8 B、7 C、6 D、45. 如图，在△ABC中，已知∠ACB=90°，点D为AB的中点，AB=6，则CD=（ ）
A、3.5 B、3 C、4 D、66. 如图，在△ABC中，∠C=90°，BD平分∠ABC，CD=3，则D到AB的距离是（ ）
A、2 B、3 C、4 D、57. 若等腰三角形的两边长分别是4和6，则它的周长是（ ）A、14 B、15 C、16 D、14或168. 若关于x的一元一次不等式(m－2)x≥m－2的解为x≤1，则m的取值范围是（ ）A、m＜2 B、m≤2 C、m＞2 D、m≥29. 如图，在△ABC中，AB＝AC，D为BC上一点，且DA＝DC，BD＝BA，则∠B的大小为（ ）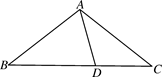
A、40° B、36° C、30° D、25°10. 如图，在Rt△ABC中，∠B=90°，AB=2，BC=1.5，延长BC至E，使得CE=BC，将△ABC沿AC翻折，使点B落点D处，连结DE，则DE的长为（ ）
A、 B、 C、 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 在△ABC中，∠A=40°，∠B=75°，则∠C=.12. “x的3倍与5的差大于9”用不等式可表示为.13. 如图，已知OA=OB，请你添加一个条件 ， 使得△AOC≌△BOD（添一个即可）.
14. 已知a＜b，则2a－22b－2.（用“＞”、“＜或＝”填空）15. 已知关于x的不等式0.5x＞3a－2.5x.若不等式的最小负整数解为x=－7，则a的取值范围是.16. 如图，已知等边△ABC的边长是12，AD⊥BC.
(1)、BD=；(2)、若点P在线段AD上运动，则AP+BP的最小值是.三、解答题（本题有8小题,第17～19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分,各小题都必须写出解答过程）
-
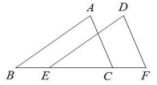
17. 解下列不等式（组）：(1)、3x－2≤2x(2)、18. 如图，点B，E，C，F在同一直线上，且AB=DE，AC=DF，BE=CF.
求证：△ABC≌△DEF
19. 如图，已知Rt△ABC中，∠ACB=90°，以BC为边作等边△BCD.
(1)、用无刻度的直尺和圆规作AB边上的中线(保留作图痕迹)；(2)、仅用无刻度的直尺作∠BDC的角平分线.20. 如图，在△ABC中，已知∠ABC和∠ACB的平分线相交于点O.过点O作DE∥BC交AB，AC于点D，点E.
(1)、求证：△BOD为等腰三角形；(2)、若BD=6，DE=11，求EC的长.21. 如图，△ABC中，∠ACB=90°，AC=BC，点C在直线l上，分别过点A，点B作AD⊥l于点D，BE⊥l于点E.
(1)、求证：BE=CD；(2)、延长AB交直线l于点F，若BF=BC，AD=3，求CF的长.22. 某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求，决定增设篮球、足球两门选修课程，需要购进一批篮球和足球.已知篮球的单价比足球的单价多30元，购买1个篮球和1个足球共需费用210元.(1)、求篮球和足球的单价分别是多少元；(2)、学校计划采购篮球、足球共50个，并要求篮球不少于30个，且总费用不超过5500元.那么有哪几种购买方案.23. 背景材料：在学习全等三角形知识时，数学兴趣小组发现这样一个模型，它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时，始终存在一对全等三角形.通过资料查询，这种模型称为“手拉手”模型.现规定：将两个等腰三角形的底角顶点连结起来的两条线段叫做“兄弟”线段.
例如：如图1，两个等腰三角形△ABC和△ADE，∠BAC=∠DAE，AB=AC，AD=AE，证得△ADB≌△AEC.此时线段DB和线段EC就是一对“兄弟”线段.
(1)、[材料理解]请判断上例中“兄弟”线段DB和EC的大小关系，并说明理由；(2)、[深入探究]如图2，△ABC和△DCE都是等腰直角三角形，且∠ACB=∠DCE=90°.连接AD，若AC=2，AD=1，∠DAC=45°，求AE的长；(3)、[延伸应用]如图3，△ABC是等腰直角三角形，∠ACB=90°，P是△ACB外一点，∠APC=75°，PC=4 ， AP=8，求线段BP的长.24. 如图，△ABC中，BA=BC，CO⊥AB于点O，AO=4，BO=6.
(1)、求BC，AC的长；(2)、若点D是射线OB上的一个动点，作直线DE⊥AC于点E，直线DE与直线BC交于点F.①如图1，当点D在线段OB上时，求证：△BDF是等腰三角形；
②连结OF，CD，若S△OBF：S△OBC=1：2，求CD的长.