广东省深圳市坪山区2023-2024学年八年级上学期数学期中试卷
试卷更新日期:2023-12-01 类型:期中考试
一、选择题。(本题共10小题,每小题3分,共30分。每小题给出4个选项,其中只有一个是正确的)
-
1. 25的算术平方根是( )A、5 B、 C、-5 D、±52. 下面各组数中,勾股数是( )A、0.3,0.4,0.5 B、1,1, C、5,12,13 D、1, , 23. 若 , 则估计m的值所在范围是( )A、1<m<2 B、2<m<3 C、3<m<4 D、4<m<54. 下列各点中,在第二象限的点是( )A、(2,3) B、(2,-3) C、(-2,3) D、(0,-2)5. 下列曲线中不能表示y是x的函数的是( )A、
 B、
B、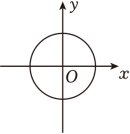 C、
C、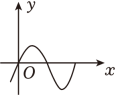 D、
D、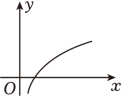 6. 下列计算正确的是( )A、=-2 B、4-3=1 C、+= D、2=7. 在平面直角坐标系中,将函数y=3x +2的图象向下平移3个单位长度,所得的函数的解析式是( )A、y=3x+5 B、y=3x﹣5 C、y=3x+1 D、y=3x﹣18. 如图,根据图中的标注和作图痕迹可知,在数轴上的点A所表示的数为( )
6. 下列计算正确的是( )A、=-2 B、4-3=1 C、+= D、2=7. 在平面直角坐标系中,将函数y=3x +2的图象向下平移3个单位长度,所得的函数的解析式是( )A、y=3x+5 B、y=3x﹣5 C、y=3x+1 D、y=3x﹣18. 如图,根据图中的标注和作图痕迹可知,在数轴上的点A所表示的数为( ) A、-1- B、-1+ C、 D、19. 如图,阴影部分表示以Rt△ABC的各边为直径的三个半圆所组成的两个新月形,面积分别记作S1和S2 . 若AC=6,BC=8,则阴影部分面积S1+S2是( )
A、-1- B、-1+ C、 D、19. 如图,阴影部分表示以Rt△ABC的各边为直径的三个半圆所组成的两个新月形,面积分别记作S1和S2 . 若AC=6,BC=8,则阴影部分面积S1+S2是( )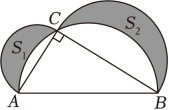 A、9π B、12.5π C、14 D、2410. 在同一平面直角坐标系中,一次函数的与的图象可能是( )A、
A、9π B、12.5π C、14 D、2410. 在同一平面直角坐标系中,一次函数的与的图象可能是( )A、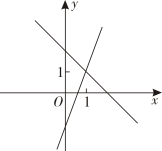 B、
B、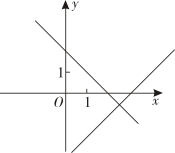 C、
C、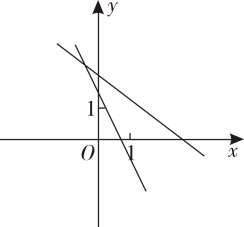 D、
D、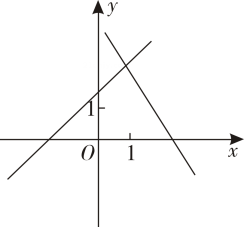
二、填空题。(本题共5小题,每小题3分,共15分)
-
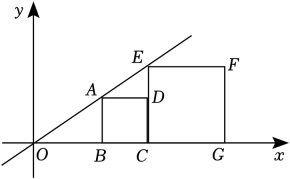
11. 实数-1的相反数是 .12. 已知平面直角坐标系中,点(2,a)和点(-2,3)关于原点对称,则a= .13. 若 , 则yx= .14. 如图,正方形ABCD , CEFG边在x轴的正半轴上,定点A、E在直线上,如果正方形ABCD边长是1,那么点F的坐标是 .
 15. 如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.若PA=AB=5米,点P到AD的距离是3米,有一只蚂蚁要从点P爬到点B , 它的最短行程是米.
15. 如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.若PA=AB=5米,点P到AD的距离是3米,有一只蚂蚁要从点P爬到点B , 它的最短行程是米.
三、解答题。(本题共7小题,其中第16题12分,第17题6分,第18题6分,第19题6分,第20题6分,第21题9分,第22题10分,共55分)
-
16. 计算:(1)、;(2)、;(3)、;(4)、 .17. 如图,在平面直角坐标系中,已知A(1,5),B(-3,0),C(-4,3).
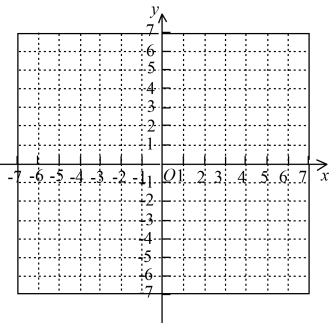 (1)、在图中作出△ABC以及关于y轴的对称图形△A1B1C1 , 并写出点A1 , B1 , C1的坐标;(2)、求△ABC的面积.18. 如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC、DB , 且CD=4,BD=3.
(1)、在图中作出△ABC以及关于y轴的对称图形△A1B1C1 , 并写出点A1 , B1 , C1的坐标;(2)、求△ABC的面积.18. 如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC、DB , 且CD=4,BD=3.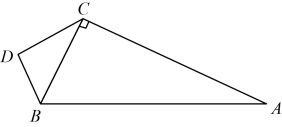 (1)、求BC的长;(2)、求证:△BCD是直角三角形.19. 如图,已知一次函数y=kx-3图象经过点M(-2,1),且与x轴交于点A,与y轴交于点B.
(1)、求BC的长;(2)、求证:△BCD是直角三角形.19. 如图,已知一次函数y=kx-3图象经过点M(-2,1),且与x轴交于点A,与y轴交于点B.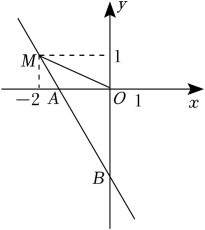 (1)、求k的值:(2)、求△AOB的面积.20. 当a=2023时,求的值.如图是小亮和小芳的解答过程:
(1)、求k的值:(2)、求△AOB的面积.20. 当a=2023时,求的值.如图是小亮和小芳的解答过程:小亮
解:原式=a+
=a+1-a=1
小芳
解:原式
=a+a-1=2a-1.
当a=2023时,原式=4045
(1)、的解法是错误的;(2)、当a=2时.求的值.21. 阅读下列一段文字,回答问题.【材料阅读】平面内两点M(x1 , y1),N(x2 , y2),则由勾股定理可得,这两点间的距离MN= .
例如.如图1,M(3,1),N(1,-2),则 .
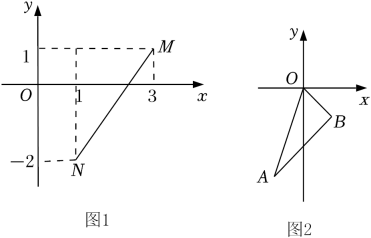
【直接应用】
(1)、已知P(2,-3),Q(-1,3),求P、Q两点间的距离;(2)、如图2,在平面直角坐标系中的两点A(-1,3),B(4,1),P为x轴上任一点,求PA+PB的最小值;(3)、利用上述两点间的距离公式,求代数式的最小值是 .22. 如图1,已知直线与直线AC:y=-2x+b交于点A(1,2),两直线与x轴分别交于点B和点C.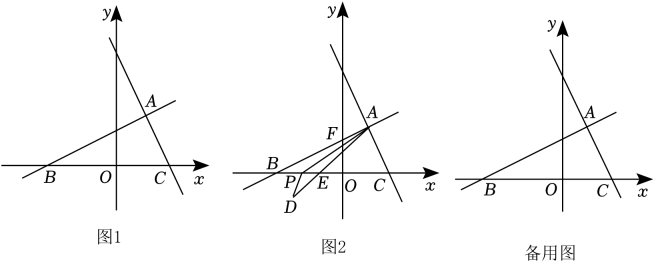 (1)、求直线AB和AC的函数表达式;(2)、求四边形AFOC的面积;(3)、如图2,点P为线段BC上一动点,将△ABP沿直线AP翻折得到△APD , 线段AD交x轴于点E.当△DPE为直角三角形时,请直接写出点P的坐标.
(1)、求直线AB和AC的函数表达式;(2)、求四边形AFOC的面积;(3)、如图2,点P为线段BC上一动点,将△ABP沿直线AP翻折得到△APD , 线段AD交x轴于点E.当△DPE为直角三角形时,请直接写出点P的坐标.