湖北省荆门市沙洋县教联体2023-2024学年九年级上学期期中考试数学试题

试卷更新日期：2023-12-01 类型：期中考试

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）

1. 若a为方程x²+2x-4＝0的解，则3a²+6a-8的值为（）

A、4 B、2 C、-4 D、-12

查看试题解析
2. 下列二次函数中，其图象的顶点坐标是(2，-1)的是（）

A、 $y = {(x - 2)}^{2} + 1$ B、 $y = {(x + 2)}^{2} + 1$ C、 $y = {(x - 2)}^{2} - 1$ D、 $y = {(x + 2)}^{2} - 1$

查看试题解析
3. 用配方法解方程x²+6x+2＝0时，配方结果正确的是（）

A、（x+3）²＝7 B、（x+3）²＝11 C、（x-3）²＝7 D、（x-3）²＝11

查看试题解析
4. 将抛物线y=x²-1先向上平移2个单位，再向右平移1个单位后所得的抛物线是（）

A、y=(x-1)²+1 B、y=(x+1)²+2 C、y=(x-2)² D、y=(x+2)²+1

查看试题解析
5. 某银行经过最近两次降息，使一年期存款的年利率由2.25%降至1.98%，设平均每次降息的百分率为x，则可列方程为（）

A、2×2.25%(1-x)=1.98% B、2.25%(1-2x)=1.98% C、1.98%(1+x)²=2.25% D、2.25%(1-x)²=1.98%

查看试题解析
6. 某大桥的桥拱可以用抛物线的一部分表示，函数关系为 $y = - \frac{1}{25} x^{2}$ ，当水面宽度AB为20m时，水面与桥拱顶的高度CO等于（）

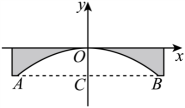A、2m B、4m C、10m D、16m

查看试题解析
7. 已知抛物线 $y = x^{2} + 2 x + 4$ 上有一点 $P (a ， b)$ ，当 $- 2 \leq a < 3$ 时，则P点纵坐标b的取值范围为（）

A、4≤b﹤19 B、-1≤b≤4 C、3≤b﹤19 D、4﹤b≤19

查看试题解析
8. 若5x²-10x+4y²=0，则x²+y²的最大值为（）

A、 $\frac{25}{4}$ B、4 C、5 D、 $\frac{25}{2}$

查看试题解析
9. 已知关于x的不等式组 $\{\begin{cases} 3 x ＞ 2 （ x - 2) \\ 3 x - \frac{x + 1}{2} \leq \frac{1}{2} a \end{cases}$ 有且只有4个整数解，且关于x的一元二次方程（a-2）x²+2x+1＝0有实数根的所有满足条件的整数a的和为（）

A、3 B、5 C、9 D、10

查看试题解析
10. 已知抛物线y＝ax²+bx+c（a，b，c为常数，a＜0）经过点（-1，0），其对称轴为直线x＝2，有下列结论：①c＜0；②4a+b＝0；③4a+c＞2b；④若y＞0，则-1＜x＜5；
⑤关于x的方程ax²+bx+c+1＝0有两个不等的实数根；⑥若M（3，y₁）与N（4，y₂）是此抛物线上两点，则y₁＞y₂ ．其中，正确结论的个数是（）

A、6 B、5 C、4 D、3

查看试题解析

二、填空题（共6小题，每小题3分，共18分）

11. 已知关于x的方程 $x^{2} - 5 x + 3 = 0$ 的两实数根分别为m，n，则 $m^{2} + n^{2} =$ .

查看试题解析
12. 从地面竖直向上抛出一小球，小球的高度h（米）与小球的运动时间t（秒）之间的关系式是h＝30t-5t²（0≤t≤6），若抛出小球1秒钟后再抛出同样的第二个小球．则第二个小球抛出秒时，两个小球在空中的高度相同．

查看试题解析
13. 已知关于x的方程a（x+m）²+b＝0（a，b，m均为常数，且a≠0）的两个解是x₁＝3和x₂＝7，则方程a(x+m+2)²⁺b=0的解是．

查看试题解析
14. 已知关于x的方程x²+（m²+1）x+4＝0的两实数根分别为α、β，
则 $α \sqrt{\frac{β}{α}} + β \sqrt{\frac{α}{β}}$ ＝．

查看试题解析
15. 已知关于x的方程kx²+（1-k）x-1=0，有下列说法：①当k=0时，方程无解；②当k=1时，方程有一个实数解；③当k=-1时，方程有两个相等的实数解；④此方程总有实数解．其中正确的是．

查看试题解析
16. 已知函数y＝mx²+3mx+m-1的图象与坐标轴恰有两个公共点，则实数m的值为．

查看试题解析

三、解答题（共8小题，共72分）

17. 解方程：

(1)、3x²-4x-1=0(公式法)

(2)、（x-1）²=2x（1-x）

查看试题解析
18. 已知 $y = a x^{2} + b x + c (a \neq 0)$ ， y与x的部分对应值如下表：
          $x$
…
-2
-1
0
2
…
          $y$
…
-3
-4
-3
5
…

(1)、求二次函数的表达式；

(2)、求该函数图象与x轴的交点坐标；

(3)、直接写出不等式 $a x^{2} + b x + c + 3 > 0$ 的解集.

查看试题解析
19. 如图，
利用一面墙（墙的长度为20米），用34米长的篱笆围成两个鸡场.中间用一道篱笆隔开，每个鸡场均留一道1米宽的门，若两个鸡场总面积为96平方米，

(1)、求AB的长.

(2)、两个鸡场的总面积可以为110平方米吗，若行求出AB的长，若不行请说明理由.

查看试题解析
20. 已知关于x的方程 $x^{2} - (m - 2) x - \frac{m^{2}}{4} = 0$ .

(1)、求证：无论m取什么值，这个方程总有两个相异的实数根.

(2)、若这个方程的两个实根满足 $x_{1} = x_{2} + 2$ ，求m的值及相应的两根.

查看试题解析
21. 已知二次函数图象顶点 $A (2 ， - 3)$ ，且过 $B (3 ， 1)$ .

(1)、求该二次函数解析式；

(2)、P为该抛物线对称轴上一点，且 $△ A B P$ 为等腰三角形，直接写出P点的所有可能坐标.

查看试题解析
22. 已知平行四边形ABCD的两边AB、AD的长是关于x的方程 $x_{}^{2} - m x + \frac{m}{2} - \frac{1}{4} = 0$ 的两实根.

(1)、当m为何值时，四边形ABCD为菱形.

(2)、若（AB-3）(AD-3)= $\frac{25}{4} m_{}^{2}$ ，求m的值

查看试题解析
23. 某商品的进价为每件40元，售价为每件50元，每个月可卖出210件，如果每件商品的售价上涨1元，则每个月少卖10件（每件售价不能高于65元），设每件商品的售价上涨 $x$ 元（ $x$ 为正整数），每个月的销售利润为 $y$ 元，

(1)、求 $y$ 与 $x$ 的函数关系式并直接写出 $x$ 的取值范围；

(2)、每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

(3)、若在销售过程中每一件商品有a（a>2）元的其他费用，商家发现当售价每件不低于58元时，每月的销售利润随 $x$ 的增大而减小，请求出 $a$ 的取值范围.

查看试题解析
24. 如图，已知抛物线 $y = - x^{2} + 2 x + 3$ 与y轴交于点C，与x轴交于A、B两点（点A在点B左边）.

(1)、请直接写出A、B、C三点的坐标；

(2)、点P是第一象限内抛物线上一点，求△PBC面积最大时点P的坐标.

(3)、如图1，已知点M在抛物线上，点N在x轴上，且四边形AMNC为平行四边形，求M点的横坐标；

查看试题解析

$x$	…	-2	-1	0	2	…
$y$	…	-3	-4	-3	5	…