广东省揭阳市榕城区2023-2024学年九年级上学期数学期中试卷

试卷更新日期：2023-12-01 类型：期中考试

进入出卷网下载

一、选择题：（每题3分，共30分）

1. 方程 $x^{2} = 3 x$ 的解是（）

A、 $x = 3$ B、 $x = 0$ C、 $x_{1} = 3$ ， $x_{2} = 0$ D、 $x_{1} = - 3$ ， $x_{2} = 0$

查看试题解析
2. 如图， $E ， F ， G ， H$ 分别是矩形 $A B C D$ 各边的中点， $A B = 6 c m$ ， $B C = 8 c m$ ，则四边形 $E F G H$ 的面积是（）

A、 $48 c m^{2}$ B、 $32 c m^{2}$ C、 $24 c m^{2}$ D、 $12 c m^{2}$

查看试题解析
3. 关于频率和概率的关系，下列说法正确的是（）.

A、频率等于概率 B、当实验次数很大时，频率稳定在概率附近 C、当实验次数很大时，概率稳定在频率附近 D、实验得到的频率与概率不可能相等

查看试题解析
4. 利用配方法解方程2x²- $\frac{4}{3}$ x-2＝0时，应先将其变形为（）

A、 $(x + \frac{1}{3})^{2} = \frac{8}{9}$ B、 $(x - \frac{1}{3})^{2} = \frac{10}{9}$ C、 $(x - \frac{1}{3})^{2} = \frac{8}{9}$ D、 $(x + \frac{1}{3})^{2} = \frac{10}{9}$

查看试题解析
5. 如图，四边形 $A B C D$ 为平行四边形，延长 $A D$ 到 $E$ ，使 $D E = A D$ ，连接 $E B$ ， $E C$ ， $D B$ ，添加一个条件，不能使四边形 $D B C E$ 成为矩形的是（）．

A、 $A B = B E$ B、 $C E ⊥ D E$ C、 $∠ A D B = 90 °$ D、 $B E ⊥ A B$

查看试题解析
6. 已知 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} - x - 10 = 0$ 的两个实根，则 $x_{1}^{3} - 10 x_{1} + x_{2}$ 的值为（）

A、10 B、11 C、12 D、21

查看试题解析
7. 如图，菱形的对角线 $A C$ ， $B D$ 相交于点 $O$ ，过点 $A$ 作 $A E ⊥ B C$ 于点 $E$ ，连接 $O E$ ，若 $O B = 6$ ，菱形 $A B C D$ 的面积为 $54$ ，则 $O E$ 的长为（）

A、 $4.5$ B、 $5$ C、 $8$ D、 $9$

查看试题解析
8. 新冠肺炎是一种传染性极强的疾病，如果有一人患病，经过两轮传染后有64人患病，设每轮传染中平均一个人传染了x个人，下列列式正确的是（）

A、 $x + x (1 + x) = 64$ B、 $1 + x + x^{2} = 64$ C、 $(1 + x)^{2} = 64$ D、 $x (1 + x) = 64$

查看试题解析
9. 在矩形 $A B C D$ 中，以A为圆心， $A D$ 长为半径画弧，交 $A B$ 于F点，以C为圆心， $C D$ 长为半径画弧，交 $A B$ 于E点，若 $A D = 2$ ， $C D = \sqrt{5}$ ，则 $E F =$ （）

A、1 B、 $4 - \sqrt{5}$ C、 $\sqrt{5} - 2$ D、 $3 - \sqrt{5}$

查看试题解析
10. 如图1，在菱形ABCD中，∠A＝60°，动点P从点A出发，沿折线AD→DC→CB方向匀速运动，运动到点B停止．设点P的运动路程为x，△APB的面积为y，y与x的函数图象如图2所示，则AB的长为（）

A、 $\sqrt{3}$ B、2 $\sqrt{3}$ C、3 $\sqrt{3}$ D、4 $\sqrt{3}$

查看试题解析

二、填空题：（每题3分，共15分）

11. 设方程 $x^{2} + x - 2 = 0$ 的两个根为 $α$ ， $β$ ，那么 $(α - 2) (β - 2)$ 的值等于．

查看试题解析
12. 从某玉米种子中抽取6批，在同一条件下进行发芽试验，有关数据如下：
种子粒数 100 400 800 1000 2000 5000
发芽种子粒数 85 318 652 793 1604 4005
发芽频率 0.850 0.795 0.815 0.793 0.802 0.801
根据以上数据可以估计，该玉米种子发芽的概率约为（精确到0.10）．

查看试题解析
13. 如图，在矩形 $A B C D$ 中， $A C$ 交 $B D$ 于点O ，且 $A B = 24 c m$ ， $B C = 10 c m$ ，将 $A C$ 绕点C顺时针旋转 $9 0^{°}$ 至 $C E$ ，连接 $A E$ ，且 $F$ 、 $G$ 分别为 $A E$ 、 $E C$ 的中点，则四边形 $O F G C$ 的面积是．

查看试题解析
14. 某航空公司有若干个飞机场，每两个飞机场之间都开辟一条航线，一共开辟了28条航线，则这个航空公司共有飞机场个．

查看试题解析
15. 如图，在平行四边形ABCD中，对角线AC ， BD相交于点O ，动点E以每秒1个单位长度的速度从点A出发沿AC方向运动，点F同时以每秒1个单位长度的速度从点C出发沿CA方向运动，若AC＝12，BD＝8，则经过秒后，四边形BEDF是矩形．

查看试题解析

三、解答题（一）：本大题共3小题，第16题10分，第17、18题各7分，共24分

16. 利用所学知识完成下列问题：

(1)、用公式法解方程： $x^{2} - 4 x = 7$ ；

(2)、设a是关于x的一元二次方程的二次项系数，b是一次项系数，c是常数项，且满足 $(a - 3)^{4} + \sqrt{b + 2} + | a + b + c | = 0$ ，求满足条件的一元二次方程．

查看试题解析
17. 在菱形 $A B C D$ 中，点E是边 $A B$ 的中点，试分别在下列两个图形中按要求仅使用无刻度的直尺作图．

(1)、在图1中，过点E作线段 $E F ∥ B C$ ，交 $C D$ 于点F ，并说明 $E F ∥ B C$ 的理由；

(2)、在图2中，连接 $B D$ ，在 $B D$ 上找一点 $P$ ，使 $P A + P E$ 的值最小（不需说明理由）．

查看试题解析
18. 如图，一农户要建一个矩形猪舍，猪舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长、宽分别为多少时，猪舍面积为80m²？

查看试题解析

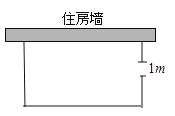
四、解答题（二）：本大题共3小题，每小题9分，共27分．

19. 某博物馆展厅的俯视示意图如图1所示，嘉淇进入展厅后开始自由参观，每走到一个十字道口，她自己可能直行，也可能向左转或向右转，且这三种可能性均相同．

(1)、求嘉淇走到王字道口A向北走的概率是；

(2)、补全图2的树状图；

(3)、借助图2的树状图分析嘉淇经过两个十字道口后向哪个方向参观的概率较大．

查看试题解析
20. 已知关于x的一元二次方程x²+（m+1）x+m＝0．

(1)、不解方程，判断方程根的情况；

(2)、若x为方程的一个根，且满足0＜x＜3，求整数m的值．

查看试题解析
21. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，过点 $C$ 的直线 $M N ∥ A B$ ， $D$ 为 $A B$ 边上一点，过点 $D$ 作 $D E ⊥ B C$ ，交直线 $M N$ 于 $E$ ，垂足为 $F$ ，连接 $C D$ ， $B E$ ．

(1)、求证： $C E = A D$ ；

(2)、当 $D$ 为 $A B$ 的中点时，判断四边形 $B E C D$ 的形状，并说明理由；

(3)、若 $D$ 为 $A B$ 的中点，则当 $∠ A =$ 时，四边形 $B E C D$ 是正方形．

查看试题解析

五、解答题（三）：本大题共2小题，每小题12分，共24分．

22. 今年是我国脱贫胜利年，我国在扶贫方面取得了巨大的成就，技术扶贫也使得我省某县的一个电子器件厂脱贫扭亏为盈．该电子器件厂生产一种电脑显卡，2019年该类电脑显卡的出厂价是200元/个，2020年，2021年连续两年在技术扶贫的帮助下改进技术，降低成本，2021年该电脑显卡的出厂价调整为162元/个．

(1)、这两年此类电脑显卡出厂价下降的百分率相同，则平均每年下降的百分率是；

(2)、 2021年某赛格电脑城以出厂价购进若干个此类电脑显卡，以200元/个销售时，平均每天可销售20个．为了减少库存，商场决定降价销售．经调查发现，单价每降低5元，每天可多售出10个，如果每天盈利1150元，单价应降低多少元？

查看试题解析
23. 如图，正方形ABCD中，E是CD边的中点，F是BC边上一点，∠FAE＝∠DAE ．

(1)、求证：AF＝AD+CF；

(2)、已知正方形ABCD的边长为4．
①求AF之长；
②若P是AE上一点，且△DEP是等腰三角形，则线段EP的长为 ▲ ．

查看试题解析

种子粒数	100	400	800	1000	2000	5000
发芽种子粒数	85	318	652	793	1604	4005
发芽频率	0.850	0.795	0.815	0.793	0.802	0.801