浙江省舟山市2023-2024学年金衢山五校联盟九年级第一学期期中质量监测数学试题卷
试卷更新日期:2023-12-01 类型:期中考试
一、选择题(本题有10小题,每小题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不给分)
-
1. 以下说法合理的是( )A、小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是 B、某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖 C、小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是 D、某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是2. 下列函数中,y是x的二次函数的是( )A、 B、 C、 D、3. 已知⊙O的半径是4,点P在⊙O内,则OP的长可能是( )A、3 B、4 C、4.5 D、54. 二次函数的开口方向、对称轴和顶点坐标分别为( )A、向下、直线、 B、向下、直线、 C、向下、直线、 D、向上、直线、5. 当时,与的图象大致可以是( )A、
 B、
B、 C、
C、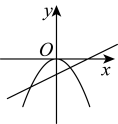 D、
D、 6. 如图,已知中, , , , , , 点D为直线上一动点,将线段绕点C顺时针旋转得到线段 , 连接、 , 点F在直线上且 , 则最小值为( )
6. 如图,已知中, , , , , , 点D为直线上一动点,将线段绕点C顺时针旋转得到线段 , 连接、 , 点F在直线上且 , 则最小值为( )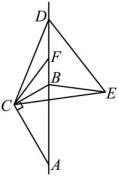 A、1 B、 C、2 D、37. 已知线段 , b,c,如果 , 那么的值是( )A、 B、 C、 D、8. 如图,一位篮球运动员投篮,球的行进路线是沿抛物线( , 的单位都为),然后准确落入篮筐内,已知篮筐的中心离地面的高度为 , 他距篮筐中心的水平距离是 , 则的值为( ).
A、1 B、 C、2 D、37. 已知线段 , b,c,如果 , 那么的值是( )A、 B、 C、 D、8. 如图,一位篮球运动员投篮,球的行进路线是沿抛物线( , 的单位都为),然后准确落入篮筐内,已知篮筐的中心离地面的高度为 , 他距篮筐中心的水平距离是 , 则的值为( ).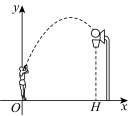 A、 B、 C、 D、9. 如图,点是以为直径的半圆的中点,连接 , 点是直径上一点,连接 , 分别过点、点向作垂线,垂足为和 , 其中, , , , 则的长是( )
A、 B、 C、 D、9. 如图,点是以为直径的半圆的中点,连接 , 点是直径上一点,连接 , 分别过点、点向作垂线,垂足为和 , 其中, , , , 则的长是( )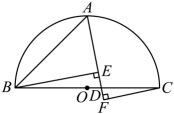 A、10 B、12. C、 D、10. 如图,在中, , , 点为边上一动点不与点、重合 , 垂直交于点 , 垂足为点 , 连接并延长交于点 , 下面结论正确的个数是( )
A、10 B、12. C、 D、10. 如图,在中, , , 点为边上一动点不与点、重合 , 垂直交于点 , 垂足为点 , 连接并延长交于点 , 下面结论正确的个数是( )①若是边上的中线,则;②若平分 , 则;③若 , 则;④的最小值为 .
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 如图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,且分别标有数字,分别转动两个转盘一次,转盘停止时(若指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止),则两个指针所指区域的数字之积为偶数的概率是 .
 12. 如图,在中,D、E分别是和上的点,且 , , , 则 .
12. 如图,在中,D、E分别是和上的点,且 , , , 则 . 13. 在半径为2的中,弦的长为2,则弦所对的圆心角的度数为 .14. 二次函数与一次函数 , 是一次函数图象上一点,是抛物线的顶点,若轴,则线段的长为 .15. 如图,正方形的边长为 , 点O为对角线交点,以各边中点为圆心,为半径依次作圆,连接点O和的中点E,则图中阴影部分的面积为 .
13. 在半径为2的中,弦的长为2,则弦所对的圆心角的度数为 .14. 二次函数与一次函数 , 是一次函数图象上一点,是抛物线的顶点,若轴,则线段的长为 .15. 如图,正方形的边长为 , 点O为对角线交点,以各边中点为圆心,为半径依次作圆,连接点O和的中点E,则图中阴影部分的面积为 . 16. 如图,已知点P是抛物线的顶点,过P作直线分别交x轴正半轴和y轴正半轴于点A、B,交抛物线于点C,且 , 过点C作轴,垂足为D,若的面积是面积的2倍,则m的为 .
16. 如图,已知点P是抛物线的顶点,过P作直线分别交x轴正半轴和y轴正半轴于点A、B,交抛物线于点C,且 , 过点C作轴,垂足为D,若的面积是面积的2倍,则m的为 .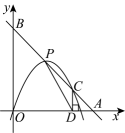
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
-
17. 已知:线段 , 且 .(1)、求的值;(2)、如果线段 , 满足 , 求的值.18. 如图,为的直径,是弦,且于点E.连接、、 .
 (1)、求证:;(2)、若 , 求弦的长.19. 如图在的网格中,的顶点都在格点上,仅用无刻度的直尺在给定的网格中分别按下列要求画图.(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示)
(1)、求证:;(2)、若 , 求弦的长.19. 如图在的网格中,的顶点都在格点上,仅用无刻度的直尺在给定的网格中分别按下列要求画图.(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示) (1)、在图1中,画出的重心G;(2)、在图2中,画线段 , 点E在上,使得;(3)、图3中,在内寻找一格点N,使 , 并标注点N的位置.20. 如图,是的弦,点是优弧的中点,连 .
(1)、在图1中,画出的重心G;(2)、在图2中,画线段 , 点E在上,使得;(3)、图3中,在内寻找一格点N,使 , 并标注点N的位置.20. 如图,是的弦,点是优弧的中点,连 . (1)、求证;(2)、若 , , 求的半径长.21. 我校举行“创建文明城市,从我做起”的征文比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.
(1)、求证;(2)、若 , , 求的半径长.21. 我校举行“创建文明城市,从我做起”的征文比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题. (1)、参加比赛的学生人数共有名,在扇形统计图中,表示“B等级”的扇形的圆心角为度,图中m的值为;(2)、补全条形统计图;(3)、组委会决定从本次比赛中获得A等级的学生中,选出两名去参加市中学生征文比赛,已知A等级中男生有2名,请用画树状图或列表的方法求出所选学生恰是一男一女的概率.22. 某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量(袋)与销售单价(元)之间的关系满足下表,另外每天还需支付其他各项费用100元.(1)、请你从学过的一次函数、二次函数、反比例函数三个模型中确定哪种函数能恰当地表示与的变化规律,并直接写出与之间的函数关系式.(2)、为了在春节前将这批干果销售完,每天的销量不能低于150袋,如果每天获得200元的利润,销售单价为多少元?(3)、若每天的销量不能低于150袋,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?23. 根据以下素材,探索完成任务.
(1)、参加比赛的学生人数共有名,在扇形统计图中,表示“B等级”的扇形的圆心角为度,图中m的值为;(2)、补全条形统计图;(3)、组委会决定从本次比赛中获得A等级的学生中,选出两名去参加市中学生征文比赛,已知A等级中男生有2名,请用画树状图或列表的方法求出所选学生恰是一男一女的概率.22. 某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量(袋)与销售单价(元)之间的关系满足下表,另外每天还需支付其他各项费用100元.(1)、请你从学过的一次函数、二次函数、反比例函数三个模型中确定哪种函数能恰当地表示与的变化规律,并直接写出与之间的函数关系式.(2)、为了在春节前将这批干果销售完,每天的销量不能低于150袋,如果每天获得200元的利润,销售单价为多少元?(3)、若每天的销量不能低于150袋,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?23. 根据以下素材,探索完成任务.
素材1 图1为某公园的抛物线型拱桥,图2是其横截面示意图,测得水面宽度米,拱顶离水面的距离为米.
素材2 拟在公园里投放游船供游客乘坐,载重最少时,游船的横截面如图3所示,漏出水面的船身为矩形,船顶为等腰三角形.测得相关数据如下:米,米,米,米.
素材3 为确保安全,拟在石拱桥下面的P,Q两处设置航行警戒线,要求如下:
①游船底部在P,Q之间通行;
②当载重最少通过时,游船顶部E与拱桥的竖直距离至少为米.
(1)、任务1 确定拱桥形状:在图2中建立合适的直角坐标系,并求这条抛物线的函数表达式.(2)、任务2 设计警戒线之间的宽度:求的最大值.24. (1)、【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明:
(1)、【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明:如图①,在矩形中, , 分别交于点E、F,分别交于点G、H,求证:;
(2)、【结论应用】如图②,将矩形沿折叠,使得点B和点D重合,若 , 求折痕的长;(3)、【拓展运用】如图③,将矩形沿折叠.使得点D落在边上的点G处,点C落在点P处,得到四边形 , 若 , 求的长.