重庆市北碚区西南大学附高2024届高三上学期数学11月月考试卷
试卷更新日期:2023-12-01 类型:月考试卷
一、单项选择题:共8小题,每小题5分,共40分。
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 若复数 , , 则( )A、 B、 C、 D、3. 已知为锐角, , 则( )A、 B、 C、 D、4. 已知 , , ( , ),为其前项和,则( )A、 B、 C、 D、5. 2023年的五一劳动节是疫情后的第一个小长假,公司筹备优秀员工假期免费旅游.除常见的五个旅游热门地北京、上海、广州、深圳、成都外,淄博烧烤火爆全国,则甲、乙、丙、丁四个部门至少有三个部门所选旅游地全不相同的方法种数共有( )A、1800 B、1080 C、720 D、3606. 对于两个函数与 , 若这两个函数值相等时对应的自变量分别为 , , 则的最小值为( )A、 B、 C、 D、7. 已知双曲线:的右焦点为 , 关于原点对称的两点A、B分别在双曲线的左、右两支上, , , 且点C在双曲线上,则双曲线的离心率为( )A、 B、 C、 D、8. 已知曲线与曲线交于点 , 则( )A、 B、 C、 D、
二、多项选择题:共4小题,每小题5分,共20分。
-
9. 已知函数 , 把的图象向左平移个单位长度得到函数的图象,则( )A、是奇函数 B、的图象关于直线对称 C、在上单调递增 D、不等式的解集为10. 袋子中有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取5次,每次取一个球.记录每次取到的数字,统计后发现这5个数字的平均数为2,方差小于1,则( )A、可能取到数字4 B、中位数可能是2 C、极差可能是4 D、众数可能是211. 如图,圆锥的底面圆的直径 , 母线长为 , 点是圆上异于 , 的动点,则下列结论正确的是( )
 A、与底面所成角为45° B、圆锥的表面积为 C、的取值范围是 D、若点为弧的中点,则二面角的平面角大小为45°12. 曲线C是平面内与两个定点 , 的距离的积等于的点P的轨迹,则下列结论正确的是( )A、曲线C关于坐标轴对称 B、点P到原点距离的最大值为 C、周长的最大值为 D、点P到y轴距离的最大值为
A、与底面所成角为45° B、圆锥的表面积为 C、的取值范围是 D、若点为弧的中点,则二面角的平面角大小为45°12. 曲线C是平面内与两个定点 , 的距离的积等于的点P的轨迹,则下列结论正确的是( )A、曲线C关于坐标轴对称 B、点P到原点距离的最大值为 C、周长的最大值为 D、点P到y轴距离的最大值为三、填空题:共4小题,每小题5分,共20分。
-
13. 若 , 则的值为14. 二项式展开式的常数项为.15. 已知数列 , 对任意正整数 , , , 成等差数列,公差为 , 则.16. 设 , 函数 , 若函数恰有3个零点,则实数的取值范围为.
四、解答题:共70分。
-
17. 在中,角A,B,C所对的边分别为a,b,c,且 .
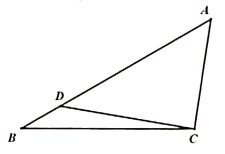 (1)、求B;(2)、已知 , D为边上的一点,若 , , 求的长.18. 已知等比数列的各项均为正数,前n项和为 , 若 , .(1)、求数列的通项公式;(2)、若 , 求数列的前n项和.19. 图1是由正方形和正三角形组成的一个平面图形,将沿折起,使点到达点的位置,为的中点,如图2.
(1)、求B;(2)、已知 , D为边上的一点,若 , , 求的长.18. 已知等比数列的各项均为正数,前n项和为 , 若 , .(1)、求数列的通项公式;(2)、若 , 求数列的前n项和.19. 图1是由正方形和正三角形组成的一个平面图形,将沿折起,使点到达点的位置,为的中点,如图2.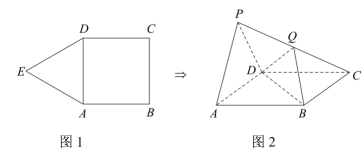 (1)、求证:平面;(2)、若平面平面 , 求平面与平面夹角的余弦值.20. 某校20名学生的数学成绩和知识竞赛成绩如下表:
(1)、求证:平面;(2)、若平面平面 , 求平面与平面夹角的余弦值.20. 某校20名学生的数学成绩和知识竞赛成绩如下表:计算可得数学成绩的平均值是 , 知识竞赛成绩的平均值是 , 并且 , , .
(1)、求这组学生的数学成绩和知识竞赛成绩的样本相关系数(精确到0.01);(2)、设 , 变量和变量的一组样本数据为 , 其中两两不相同,两两不相同.记在中的排名是第位,在中的排名是第位,.定义变量和变量的“斯皮尔曼相关系数”(记为)为变量的排名和变量的排名的样本相关系数.(i)记 , .证明:;
(ii)用(i)的公式求得这组学生的数学成绩和知识竞赛成绩的“斯皮尔曼相关系数”约为0.91,简述“斯皮尔曼相关系数”在分析线性相关性时的优势.
注:参考公式与参考数据.
;;.