云南省昆明市呈贡区西南联大研究院附中2023-2024学年八年级上学期数学期中考试试卷

试卷更新日期：2023-12-01 类型：期中考试

进入出卷网下载

一、单选题（本大题共10小题，共30分。在每小题列出的选项中，选出符合题目的一项）

1. 下列图形中，不是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段，能组成三角形的是（）

A、1、1、2 B、3、4、5 C、1、4、6 D、2、3、7

查看试题解析
3. 如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪的三个顶点的距离相等，凉亭的位置应选在（　　）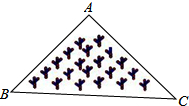

A、△ABC三边的垂直平分线的交点 B、△ABC的三条中线的交点 C、△ABC三条角平分线的交点 D、△ABC三条高所在直线的交点

查看试题解析
4. 下列计算正确的是（　　）

A、a⁹÷a³＝a（a≠0） B、（-2ab²）³＝-6a³b⁶ C、3b³•2b²＝6b⁵ D、2a²-a²＝2

查看试题解析
5. 已知图中的两个三角形全等，则∠1等于（　　）

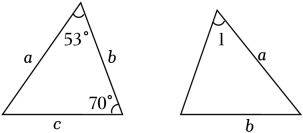A、57° B、53° C、60° D、70°

查看试题解析
6. 如图，三角形纸片ABC，AB=12，BC=8，AC=7，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为（　　）

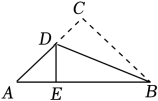A、10 B、11 C、12 D、13

查看试题解析
7. 某人到瓷砖商店去买一种多边形状的瓷砖，用来铺设无缝地板，他购买的瓷砖形状不能是（　　）

A、正三角形 B、正方形 C、正五边形 D、正六边形

查看试题解析
8. 使（x²+mx）（x²-2x+n）的乘积不含x³和x² ，则m、n的值为（　　）

A、m＝0，n＝0 B、m＝-2，n＝-4 C、m＝2，n＝4 D、m＝-2，n＝4

查看试题解析
9. 师傅和徒弟两人每小时一共做40个零件，在相同的时间内，师傅做了300个零件，徒弟做了100个零件．师傅每小时做了多少个零件？若设师傅每小时做了x个零件，则可列方程为（　　）

A、 $\frac{300}{x} = \frac{100}{40 - x}$ B、 $\frac{300}{40 - x} = \frac{100}{x}$ C、 $\frac{300}{x} = \frac{100}{x - 40}$ D、 $\frac{300}{x - 40} = \frac{100}{x}$

查看试题解析
10. 如图，正方形ABCD和长方形AEFG的面积相等，且四边形BEFH也是正方形，欧几里得在《几何原本》中利用该图得到了：BH²=CH×GH．设AB=a，CH=b.若ab=5，则图中阴影部分的周长是（　　）

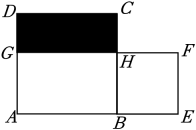A、6 B、8 C、10 D、20

查看试题解析

二、填空题（本大题共6小题，共18分。）

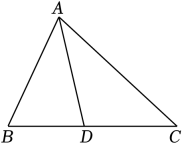
11. 近几年我国芯片产业出现被卡脖子的情况，其实中国半导体的芯片设计能力已经很强，主要问题和难点在制造环节．目前我国只能做到0.000000014米的制程，用科学记数法将0.000000014可表示为．

查看试题解析
12. 若 $m - \frac{1}{m} = 3$ ，则 $m^{2} + \frac{1}{m^{2}} =$ ．

查看试题解析
13. 已知点A（a ， -2）与点B（-3，b）关于x轴对称，则a+b的值为．

查看试题解析
14. 如图，点D是BC的中点，若△ABC的面积为6，则△ADC的面积为．

查看试题解析
15. 如图，将△ABC沿CB边向右平移得到△DFE，DE交AB于点G．已知∠A：∠C：∠ABC=1：2：3，AB=9cm，BF=5cm，AG=5cm，则图中阴影部分的面积为 cm² ．

查看试题解析
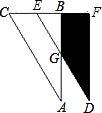16. 如图，四边形ABCD中，∠BCD=90°，∠ABD=∠DBC，AB=5，DC=6，则△ABD的面积为．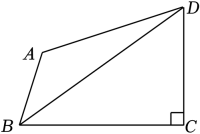

查看试题解析

三、解答题（本大题共8小题，共52分。解答应写出文字说明，证明过程或演算步骤）

17. 因式分解：

(1)、ax²-a；

(2)、6xy²-9x²y-y³ ．

查看试题解析
18. 计算：

(1)、（2a²）³+（-3a³）²；

(2)、（x+3y）（x-y）．

查看试题解析
19. 解方程．

(1)、 $\frac{x}{2 x - 1} + \frac{2}{1 - 2 x} = 3$ ；

(2)、 $\frac{4}{x^{2} - 4} - \frac{1}{x - 2} = 0$ ．

查看试题解析
20. 在如图所示的正方形网格中，每个小正方形的边长都是1，已知△ABC的三个顶点的坐标分别为A（-3，3），B（-1，1），C（-5，-3）．
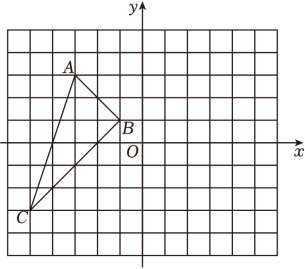
$(1)$ 画出△ABC关于y轴成轴对称的△A₁B₁C₁ ，并写出点A₁的坐标；
$(2)$ 请直接写出△A₁B₁C₁的面积；
$(3)$ 在y轴上找一点P ，使PA＝PB ，并写出点P的坐标．

查看试题解析
21. 如图，在△ABC中，AD是角平分线，∠B=54°，∠C=76°．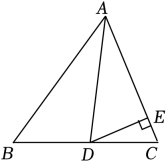

(1)、求∠BAD的度数；

(2)、若DE⊥AC ，求∠EDC的度数．

查看试题解析
22. 如图，点D，E分别在AB，AC上，且AD=AE，∠ADC=∠AEB．求证：BE=CD．

查看试题解析
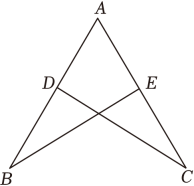23. 昭通苹果和天麻美味可口，小明在昆明某超市购买1市斤昭通苹果和2市斤小草坝天麻需要支付105元，购买3市斤昭通苹果和5市斤小草坝天麻需要265元．

(1)、1市斤昭通苹果和1市斤小草坝天麻的单价分别是多少元？

(2)、昆明到昭通的距离大约350km，以前超市老板都会亲自去往昭通选果，但今年的疫情原因，只能选择专车托运，以前花240元进购的苹果现在要花300元，进货单价比原来贵了1元，原来1市斤苹果进货单价为多少？

查看试题解析
24. 如图（1），AB=4cm，AC⊥AB，BD⊥AB，AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t（s）．

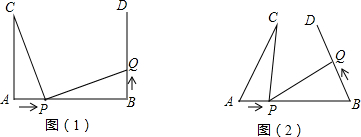(1)、若点Q的运动速度与点P的运动速度相等，当t=1时，△ACP与△BPQ是否全等，请说明理由，并判断此时线段PC和线段PQ的位置关系；

(2)、如图（2），将图（1）中的“AC⊥AB ， BD⊥AB”改为“∠CAB=∠DBA=60°”其他条件不变．设点Q的运动速度为xcm/s ，是否存在实数x ，使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明理由。

查看试题解析