安徽省蚌埠市怀远县2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-01 类型:期中考试
一、选择题(本大题共10小题,每小题4分,满分40分)
-
1. 下列函数解析式中,一定为二次函数的是( )A、 B、 C、 D、2. 下列各点中,在反比例函数的图象上的是( )A、 B、 C、 D、3. 已知点 , , 都在反比例函数的图象上,则( )A、 B、 C、 D、4. 如果两个相似三角形的周长比是1:2 , 那么它们的面积比是( )A、1:2 B、1:4 C、1: D、 :15. 已知二次函数y与自变量x的部分对应值如表:
x
…
0
1
3
4
8
…
y
…
7
0
0
40
…
则二次函数的对称轴是( )
A、 B、 C、 D、6. 主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.如图,若舞台AB长20米,主持人从舞台一侧进人,设他至少走x米时恰好站在舞台的黄金分割点上(BP长为x),则x满足的方程是( ) A、 B、 C、 D、以上都不对7. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( )
A、 B、 C、 D、以上都不对7. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( ) A、 B、1 C、 D、28. 下表列出了函数中自变量x与函数y的部分对应值.根据表中数据,判断一元二次方程的一个解在哪两个相邻的整数之间( )
A、 B、1 C、 D、28. 下表列出了函数中自变量x与函数y的部分对应值.根据表中数据,判断一元二次方程的一个解在哪两个相邻的整数之间( )x
0
1
2
y
1
2
1
A、1与2之间 B、与之间 C、与0之间 D、0与1之间9. 关于x的二次函数的图象与x轴有两个不同的交点,则m的取值范围是( )A、 B、且 C、 D、且10. 已知a,b,c为非零实数,且满足 , 则一次函数的图象一定经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 抛物线向左平移3个单位,所得的新抛物线的解析式为 .12. 已知三条线段、、 , 其中 , , 是、的比例中项,则cm.13. 二次函数的图象如图所示,则关于x的方程的一根为 , 则另一根.
 14. 如图,在矩形ABCD中, , 点E为边AD上一点, , F为BE的中点.
14. 如图,在矩形ABCD中, , 点E为边AD上一点, , F为BE的中点. (1)、.(2)、若 , CE,DF相交于点O,则.
(1)、.(2)、若 , CE,DF相交于点O,则.三、(本大题共2小题,每小题8分,满分16分)
-
15. 已知二次函数图象的顶点坐标为 , 且过点.求该二次函数的解析式.16. 已知实数x、y、z满足 ,试求 的值.
四、(本大题共2小题,每小题8分,满分16分)
-
17. 已知抛物线 , 当时,求该函数的最大值.18. 如图,在中, , AD是斜边BC上的高.
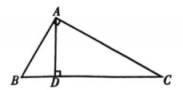 (1)、证明:;(2)、若 , , 求BD的长.
(1)、证明:;(2)、若 , , 求BD的长.五、(本大题共2小题,每小题10分,满分20分)
-
19. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题.
 (1)、写出方程ax2+bx+c=0的根;(2)、写出不等式ax2+bx+c<0的解集;(3)、若方程ax2+bx+c=k无实数根,写出k的取值范围.20. 已知反比例函数的图象经过点.(1)、求k的值;(2)、点 , 均在反比例函数的图象上,若 , 直接写出 , 的大小关系.
(1)、写出方程ax2+bx+c=0的根;(2)、写出不等式ax2+bx+c<0的解集;(3)、若方程ax2+bx+c=k无实数根,写出k的取值范围.20. 已知反比例函数的图象经过点.(1)、求k的值;(2)、点 , 均在反比例函数的图象上,若 , 直接写出 , 的大小关系.六、(本题满分12分)
-
21. 如图,已知二次函数图象经过点和 .
 (1)、求该二次函数的表达式及图象的顶点坐标.(2)、当时,请根据图象直接写出x的取值范围.
(1)、求该二次函数的表达式及图象的顶点坐标.(2)、当时,请根据图象直接写出x的取值范围.七、(本题满分12分)
-
22. 如图,平行四边形ABCD中,点E是AD的中点,连接CE并延长交BA的延长线于点F.
 (1)、求证:;(2)、点G是线段AF上一点,连接CG,满足 , OG交AD于点H,若 , , 求GH的长.
(1)、求证:;(2)、点G是线段AF上一点,连接CG,满足 , OG交AD于点H,若 , , 求GH的长.八、(本题满分14分)
-
23. 如图1所示的某种投石车是古代一种远程攻击的武器,发射出去的石块的运动轨迹是抛物线的一部分,且距离发射点20米时达到最大高度10米.将投石车置于山坡底部O处,山坡上有一点A,点A与点O的水平距离为30米,与地面的竖直距离为3米,AB是高度为3米的防御墙.若以点O为原点,建立如图2所示的平面直角坐标系.
 (1)、求石块运动轨迹所在抛物线的解析式;(2)、试通过计算说明石块能否飞越防御墙AB;(3)、在竖直方向上,试求石块飞行时与坡面OA的最大距离
(1)、求石块运动轨迹所在抛物线的解析式;(2)、试通过计算说明石块能否飞越防御墙AB;(3)、在竖直方向上,试求石块飞行时与坡面OA的最大距离
-
-