安徽省六安市 2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-01 类型:期中考试
一、选择题(本大题共10小题,每小题4分,满分40分)
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 有一个圆的半径为5,则该圆的弦长不可能是( )A、1 B、4 C、10 D、113. 将一元二次方程化成的形式,则( )A、-1 B、-2023 C、1 D、20234. 小区新增了一家快递店,第一天揽件200件,第三天揽件242件,设该快递店揽件日平均增长率为x,根据题意,下面所列方程正确的是( )A、 B、 C、 D、5. 如图,在正方形网格中,将绕某一点旋转某一角度得到 , 则旋转中心是( )
2. 有一个圆的半径为5,则该圆的弦长不可能是( )A、1 B、4 C、10 D、113. 将一元二次方程化成的形式,则( )A、-1 B、-2023 C、1 D、20234. 小区新增了一家快递店,第一天揽件200件,第三天揽件242件,设该快递店揽件日平均增长率为x,根据题意,下面所列方程正确的是( )A、 B、 C、 D、5. 如图,在正方形网格中,将绕某一点旋转某一角度得到 , 则旋转中心是( ) A、点A B、点B C、点C D、点D6. 若直线经过第一、三、四象限,则抛物线的顶点必在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 已知关于x的一元二次方程有一个非零实数根c , 则的值为( )A、1 B、-1 C、0 D、28. 已知点 , , 都在抛物线上, , 下列选项正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则9. 如图,AB为的直径,点D是的中点,过点D作于点E , 延长DE交于点F . 若 , , 则的直径长为( )
A、点A B、点B C、点C D、点D6. 若直线经过第一、三、四象限,则抛物线的顶点必在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 已知关于x的一元二次方程有一个非零实数根c , 则的值为( )A、1 B、-1 C、0 D、28. 已知点 , , 都在抛物线上, , 下列选项正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则9. 如图,AB为的直径,点D是的中点,过点D作于点E , 延长DE交于点F . 若 , , 则的直径长为( ) A、 B、8 C、10 D、10. 如图,等边的边长为4,直线l经过点A且直线 , 直线l从点A出发沿A-C以1cm/s的速度向点C移动,直到经过点C即停止,直线l分别与AB或BC交于点M , 与AC交于点N , 若的面积为y(cm),直线l的移动时间为x(s),则下面最能反映y与x之间函数关系的大致图象是( )
A、 B、8 C、10 D、10. 如图,等边的边长为4,直线l经过点A且直线 , 直线l从点A出发沿A-C以1cm/s的速度向点C移动,直到经过点C即停止,直线l分别与AB或BC交于点M , 与AC交于点N , 若的面积为y(cm),直线l的移动时间为x(s),则下面最能反映y与x之间函数关系的大致图象是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 关于x的方程的一个根为-2,则另一个根是 .12. 已知和关于原点对称,则a+b= .13. 如图1是某地公园的一座抛物线型拱桥,按如图2所示建立坐标系,得到函数 , 在正常水位时水面宽米,当水位上升5米时,则水面宽米.

图1 图2
14. 如图,在⊙O中,已知AB是直径,P为AB上一点(P不与A , B两点重合),弦MN过点P , . (1)、若 , , 则MN的长为;(2)、当点P在AB上运动时(保持不变),则 .
(1)、若 , , 则MN的长为;(2)、当点P在AB上运动时(保持不变),则 .三、(本大题共2小题,每小题8分,满分16分)
-
15. 解方程:(1)、;(2)、 .16. 已知抛物线的顶点是 , 且经过点 , 求该抛物线的函数解析式.
四、(本大题共2小题,每小题8分,满分16分)
-
17. 如图, , 是的两条弦,且 , , D为弦所对优弧上一点,求的度数.
 18. 如图,在中, , 将逆时针旋转后得到 , C点落在BD边上, , 求的度数.
18. 如图,在中, , 将逆时针旋转后得到 , C点落在BD边上, , 求的度数.
五、(本大题共2小题,每小题10分,满分20分)
-
19. 如图,AB为的弦,点C在AB上, , , 交于点D , 求CD的长.
 20. 我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.(1)、求抛物线与x轴的“和谐值”;(2)、求抛物线与直线的“和谐值”.
20. 我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.(1)、求抛物线与x轴的“和谐值”;(2)、求抛物线与直线的“和谐值”.六、(本题满分12分)
-
21. 如图,用一段77米的篱笆围成三个一边靠墙、大小相同的矩形羊圈,每个矩形都有一个l米的门,墙的最大可用长度为30米.
 (1)、如果羊圈的总面积为300平方米,求边AB的长;(2)、羊圈的总面积能为500平方米吗?若能,请求出边AB的长;若不能,请说明理由.
(1)、如果羊圈的总面积为300平方米,求边AB的长;(2)、羊圈的总面积能为500平方米吗?若能,请求出边AB的长;若不能,请说明理由.七、(本题满分12分)
-
22. 第31届世界大学生夏季运动会将于2023年7月28日至8月8日在成都举行,大熊猫是成都最具特色的对外传播标识物和“品牌图腾”,是天府之国享有极高知名度的个性名片.此次成都大运会吉祥物“蓉宝”(如图1)便是以熊猫基地真实的大熊猫“芝麻”为原型创作的.某商店销售“蓉宝”的公仔毛绒玩具,进价为30元/件,经市场调查发现:该商品的月销售量y(件)与销售价x(元/件)之间的关系如图2所示.

图1 图2
(1)、求y关于x的函数解析式;(2)、由于某种原因,该商品进价提高了a元/件(),如果规定该玩具售价不超过40元/件,该商品在今后的销售中,月销售量与销售价仍然满足(1)中的函数关系,若该商品的月销售最大利润是2400元,求a的值.八、(本题满分14分)
-
23. 如图,等腰内接于 , AC的垂直平分线交边BC于点E , 交于F , 垂足为D , 连接AF并延长交BC的延长线于点P .
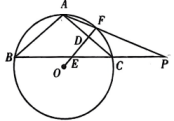 (1)、求证:;(2)、若 , 求的度数.
(1)、求证:;(2)、若 , 求的度数.
-
-