安徽省淮南市东部地区2023-2024学年八年级上学期期中数学试题
试卷更新日期:2023-12-01 类型:期中考试
一、选择题(本大题共10小题,每题4分,共40分)
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 将下列长度的三根木棒首尾顺次连接,不能组成三角形的是( )A、4、5、6 B、3、4、5 C、2、3、4 D、1、2、33. 一个多边形的内角和是外角和的2倍,这个多边形是( )A、四边形 B、五边形 C、六边形 D、八边形4. 下列各图中,作△ABC边AC上的高,正确的是( )A、
2. 将下列长度的三根木棒首尾顺次连接,不能组成三角形的是( )A、4、5、6 B、3、4、5 C、2、3、4 D、1、2、33. 一个多边形的内角和是外角和的2倍,这个多边形是( )A、四边形 B、五边形 C、六边形 D、八边形4. 下列各图中,作△ABC边AC上的高,正确的是( )A、 B、
B、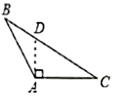 C、
C、 D、
D、 5. 将一副三角尺按如图所示的方式摆放,则∠α的大小为( )
5. 将一副三角尺按如图所示的方式摆放,则∠α的大小为( )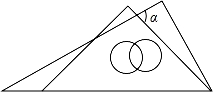 A、85° B、75° C、65° D、60°6. 工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA , OB上分别取OM=ON , 移动角尺,使角尺两边相同的刻度分别与点M , N正合,过角尺顶点C连OC . 可知△OMC≌△ONC , OC便是∠AOB的平分线.则△OMC≌△ONC的理由是( )
A、85° B、75° C、65° D、60°6. 工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA , OB上分别取OM=ON , 移动角尺,使角尺两边相同的刻度分别与点M , N正合,过角尺顶点C连OC . 可知△OMC≌△ONC , OC便是∠AOB的平分线.则△OMC≌△ONC的理由是( ) A、SSS B、SAS C、AAS D、HL7. 如图,已知AO=CO,那么添加下列一个条件后,仍无法判定△ABO ≌△CDO 的是( )
A、SSS B、SAS C、AAS D、HL7. 如图,已知AO=CO,那么添加下列一个条件后,仍无法判定△ABO ≌△CDO 的是( ) A、∠A=∠C B、BO=DO C、AB=CD D、∠B=∠D8. 下列说法中,正确的个数有( )
A、∠A=∠C B、BO=DO C、AB=CD D、∠B=∠D8. 下列说法中,正确的个数有( )①若一个多边形的外角和等于360°,则这个多边形的边数为4;
②三角形的高相交于三角形的内部;
③三角形的一个外角大于任意一个内角;
④一个多边形的边数每增加一条,这个多边形的内角和就增加 ;
⑤对角线共有5条的多边形是五边形.
A、1个 B、2个 C、3个 D、4个9. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )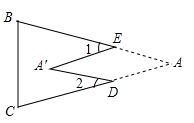 A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2(∠1+∠2)10. 如图,在△AOB和△COD中,OA=OB , OC=OD , OA<OC , ∠AOB=∠COD=36°.连接AC , BD交于点M , 连接OM . 下列结论:
A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2(∠1+∠2)10. 如图,在△AOB和△COD中,OA=OB , OC=OD , OA<OC , ∠AOB=∠COD=36°.连接AC , BD交于点M , 连接OM . 下列结论:①∠AMB=36°,②AC=BD , ③OM平分∠AOD , ④MO平分∠AMD . 其中正确的结论个数有( )个.
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题(本大题共6小题,每题4分,共24分)
-
11. 若一扇窗户打开后,用窗钩将其固定,主要运用的几何原理是 .12. 如图所示的方格中,∠1+∠2+∠3=度.
 13. 如图,在中, , 的垂直平分线交于M , 交于E , 的垂直平分线交于N , 交于F , 则的周长为 cm.
13. 如图,在中, , 的垂直平分线交于M , 交于E , 的垂直平分线交于N , 交于F , 则的周长为 cm.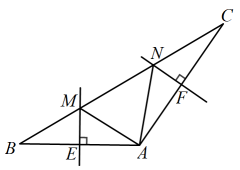 14. 如图,已知△ABC的周长是10,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=1,则△ABC的面积是 .
14. 如图,已知△ABC的周长是10,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=1,则△ABC的面积是 .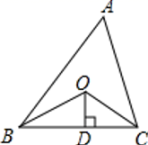 15. 如图,在中, , 和的平分线交于点 , 得 , 和的平分线交于点 , 得 , 则度.
15. 如图,在中, , 和的平分线交于点 , 得 , 和的平分线交于点 , 得 , 则度. 16. 如图,中,、的角平分线、交于点 , 延长、 , 于 , 于 , 则下列结论:①平分;②;③;④ . 其中正确结论序号是 .
16. 如图,中,、的角平分线、交于点 , 延长、 , 于 , 于 , 则下列结论:①平分;②;③;④ . 其中正确结论序号是 .
三、解答题(本大题共6小题,共56分)
-
17. 如图,已知OA和OB是两条公路,C , D是两个村庄,建立一个车站M , 使车站到两个村庄距离相等,即MC=MD , 且M到OA , OB两条公路的距离相等.请用尺规作图法作出点M的位置.(保留作图痕迹,不写作法)
 18. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D。
18. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D。 19. 如图所示,在△ABC中,AE是角平分线,AD是高,∠BAC=80°,∠EAD=10°,求∠B的度数
19. 如图所示,在△ABC中,AE是角平分线,AD是高,∠BAC=80°,∠EAD=10°,求∠B的度数 20. △ABC在平面直角坐标系中的位置如图所示(每个小正方形的边长为1).
20. △ABC在平面直角坐标系中的位置如图所示(每个小正方形的边长为1). (1)、作出△ABC关于y轴对称的△A1B1C1;(2)、直接写出点C1的坐标;(3)、若P(a,a-1)是△ABC内部一点,点P关于y轴对称点为P',且PP’=6,求点P'的坐标.
(1)、作出△ABC关于y轴对称的△A1B1C1;(2)、直接写出点C1的坐标;(3)、若P(a,a-1)是△ABC内部一点,点P关于y轴对称点为P',且PP’=6,求点P'的坐标.

