(第一次学期同步) 6.1几何图形—2023-2024学年浙教版七年级数学
试卷更新日期:2023-11-30 类型:同步测试
一、选择题
-
1. 围成下列这些立体图形的各个面中,都是平的面为( )A、
 B、
B、 C、
C、 D、
D、 2. 下列几何体中,不是柱体的是( )A、
2. 下列几何体中,不是柱体的是( )A、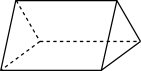 B、
B、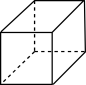 C、
C、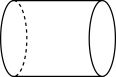 D、
D、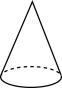 3. 如图所示的平面图形绕直线I旋转一周,可以得到的立体图形是( )
3. 如图所示的平面图形绕直线I旋转一周,可以得到的立体图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. “力箭一号”(ZK-1A)运载火箭在酒泉卫星发射中心采用“一箭六星”的方式,成功将六颗卫星送入预定轨道,则卫星在预定轨道飞行留下的痕迹体现了( )A、点动成线 B、线动成面 C、面动成体 D、面面相交成线5. 周末,小明和小亮相约去某公园游玩,中途两人口渴了,于是小明提议通过在地面旋转硬币的方法决定谁去买水,在旋转硬币时小明发现:当硬币在地面某位置快速旋转时,形成了一个几何体,则这个几何体是( )A、圆锥 B、圆柱 C、球 D、正方体6. 下列各图中表示立体图形的是( )A、
4. “力箭一号”(ZK-1A)运载火箭在酒泉卫星发射中心采用“一箭六星”的方式,成功将六颗卫星送入预定轨道,则卫星在预定轨道飞行留下的痕迹体现了( )A、点动成线 B、线动成面 C、面动成体 D、面面相交成线5. 周末,小明和小亮相约去某公园游玩,中途两人口渴了,于是小明提议通过在地面旋转硬币的方法决定谁去买水,在旋转硬币时小明发现:当硬币在地面某位置快速旋转时,形成了一个几何体,则这个几何体是( )A、圆锥 B、圆柱 C、球 D、正方体6. 下列各图中表示立体图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,用一个平面去截圆锥,得到的截面是( )
7. 如图,用一个平面去截圆锥,得到的截面是( ) A、
A、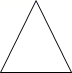 B、
B、 C、
C、 D、
D、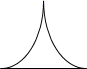 8. 如图所示的长方形(长为7,宽为4)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( )
8. 如图所示的长方形(长为7,宽为4)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( ) A、22 B、5 C、7 D、119. 已知一不透明的正方体的六个面上分别写着至六个数字,如图是我们能看到三种情况,那么和的对面数字分别是( )
A、22 B、5 C、7 D、119. 已知一不透明的正方体的六个面上分别写着至六个数字,如图是我们能看到三种情况,那么和的对面数字分别是( )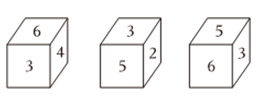 A、 , B、 , C、 , D、 ,10.
A、 , B、 , C、 , D、 ,10.如图所示,则图中三角形的个数一共是( )
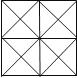 A、16 B、32 C、40 D、44
A、16 B、32 C、40 D、44二、填空题
-
11. 流星划过夜空,会留下一条长长的“尾巴”,用数学知识解释这一现象:.12. 下列儿何体中,属于棱柱的有(填序号).
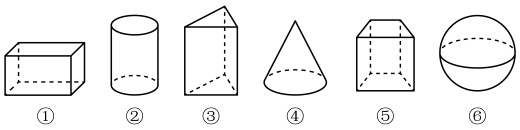 13. 将一个直角三角形ABC绕它的一边旋转,旋转后所得的几何体可能是下面图中的哪个 .
13. 将一个直角三角形ABC绕它的一边旋转,旋转后所得的几何体可能是下面图中的哪个 . 14. 用一个平面去截长方体,三棱柱,圆柱,和圆锥,其中不能截出三角形的几何体.15. 如图,模块①由15个棱长为1的小正方体构成,模块②一⑥均由4个棱长为1的小正方体构成,现在从模块②一⑥中选出三个模块放到模块①上,与模块①组成一个棱长为3的大正方体,则符合上述要求的三个模块序号是 .
14. 用一个平面去截长方体,三棱柱,圆柱,和圆锥,其中不能截出三角形的几何体.15. 如图,模块①由15个棱长为1的小正方体构成,模块②一⑥均由4个棱长为1的小正方体构成,现在从模块②一⑥中选出三个模块放到模块①上,与模块①组成一个棱长为3的大正方体,则符合上述要求的三个模块序号是 .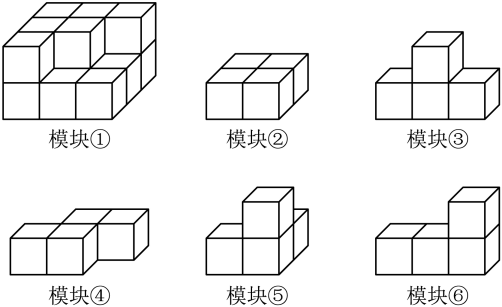 16. 用棱长是1cm的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是cm2.
16. 用棱长是1cm的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是cm2.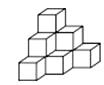
三、解答题
-
17. 找出与下面立体图形的实物,用线连起来.
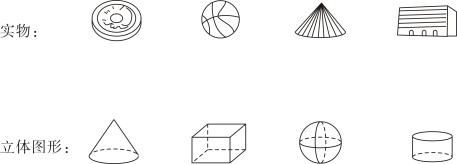 18. 如图,将第一行中的每个图形分别绕虚线旋转一周,便能形成第二行中相应的一个几何体,请你把有对应关系的图形用线连一连.
18. 如图,将第一行中的每个图形分别绕虚线旋转一周,便能形成第二行中相应的一个几何体,请你把有对应关系的图形用线连一连. 19. 一块长方形铁皮,长25厘米,宽15厘米,从四个角分别剪去边长2厘米的小正方形,然后把四周折起来,做成没有盖子的铁盒,铁盒的容积是多少升?
19. 一块长方形铁皮,长25厘米,宽15厘米,从四个角分别剪去边长2厘米的小正方形,然后把四周折起来,做成没有盖子的铁盒,铁盒的容积是多少升?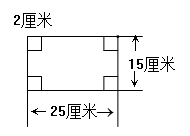 20.
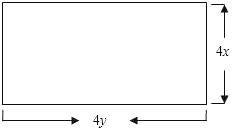
20.人人争当小小设计师.一个工程队为建设一项重点工程,要在一块长方形荒地上建造几套简易住房,每一套简易住房的平面是由长4y、宽4x构成,要求建成:两室、一厅、一厨、一卫.其中客厅面积为6xy;两个卧室的面积和为8xy;厨房面积为xy;卫生间面积为xy.请你根据所学知识,在所给图中设计其中一套住房的平面结构示意图.
 21.
21.将一个正方体木块涂成红色,然后如图把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体.观察并回答下列问题:
(1)其中三面涂色的小正方体有 个,两面涂色的小正方体有 个,各面都没有涂色的小正方体有 个;
(2)如果将这个正方体的棱n等分,所得的小正方体中三面涂色的有 个,各面都没有涂色的有 个;
(3)如果要得到各面都没有涂色的小正方体100个,那么至少应该将此正方体的棱 等分.
 22. 从棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体,得到一个如图的零件,求:
22. 从棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体,得到一个如图的零件,求: (1)、这个零件的表面积(包括底面);
(1)、这个零件的表面积(包括底面);
(2)、这个零件的体积.23. 如图1,现有一个棱长为20cm的立方体水槽放在桌面上,水槽内水的高度为acm,往水槽里放入棱长为10cm的立方体铁块. (1)、求下列两种情况下a的值.
(1)、求下列两种情况下a的值.①若放入铁块后水面恰好在铁块的上表面,则a=cm;②若放入铁块后水槽恰好盛满(无溢出),则a=cm;
(2)、若0≤a≤7.5,放入铁块后水槽内水面的高度为cm,(用含a的代数式表示).(3)、如图2,在水槽旁用管子连通一个底面在桌面上的圆柱形容器,内部底面积为50cm2 , 管口底部A离水槽内底面的高度为hcm (h>a),水槽内放入铁块,水溢入圆柱形容器后,容器内水面与水槽内水面的高度差为4cm,若 a=15,求h的值.(水槽和容器的壁及底面厚度相同)