（第一次学期同步） 5.4一元一次方程的应用—2023-2024学年浙教版七年级数学

试卷更新日期：2023-11-30 类型：同步测试

进入出卷网下载

一、选择题

1. 如果 $5 （ x - 2 ）$ 与 $2 （ x - 3 ）$ 互为相反数，那么x的值是（）

A、 $\frac{16}{7}$ B、 $\frac{7}{16}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
2. 根据下面所给条件，能列出方程的是（）

A、一个数的 $\frac{1}{3}$ 是6 B、x与1的差的 $\frac{1}{4}$ C、甲数的2倍与乙数的 $\frac{1}{3}$ D、a与b的和的60%

查看试题解析
3. 如图，数轴上的点O和点A分别表示0和10，点P是线段 $O A$ 上一动点．点P从点O出发沿 $O \to A$ 的方向以每秒2个单位的速度向A运动，B是线段 $O A$ 的中点，设点P运动时间为t秒（t不超过5秒）．若点P在运动过程中，当 $P B = 2$ 时，则运动时间t的值为____．

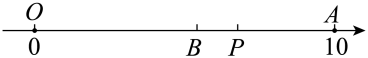A、 $\frac{7}{2}$ 秒 B、 $\frac{3}{2}$ 秒 C、3秒或7秒 D、 $\frac{3}{2}$ 秒或 $\frac{7}{2}$ 秒

查看试题解析
4. 把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本.若设这个班有x名学生，可列出的方程为（）

A、 $3 x + 20 = 4 x - 25$ B、 $3 (x + 20) = 4 (x - 25)$ C、 $3 x - 25 = 4 x + 20$ D、 $3 x - 20 = 4 x + 25$

查看试题解析
5. 我国古代数学著作《孙子算经》卷中记载“多人共车”问题，原文如下：“今有三人共车，二车空；二人共车，九人步，问人与车各几何？”意思是：今有若干人乘车，每3人乘1车，最终剩余2辆车；若每2人共乘1车，最终剩余9个人无车可乘，问有多少人，多少辆车？设有x个人，根据题意列方程正确的是（）

A、 $\frac{x}{3} + 2 = \frac{x}{2} + 9$ B、 $\frac{x}{3} + 2 = \frac{x - 9}{2}$ C、 $\frac{x - 2}{3} = \frac{x - 9}{2}$ D、 $\frac{x - 2}{3} = \frac{x}{2} + 9$

查看试题解析
6. 一项工程，甲独做3天完成，乙独做7天完成，两人共同合作，需x天完成，可列方程（）

A、3x+7x=1 B、 $\frac{x}{3} + \frac{x}{7}$ =1 C、( $\frac{1}{3} - \frac{1}{7}$ )x=1 D、x=( $\frac{1}{3} - \frac{1}{7}$ )-1

查看试题解析
7. 王先生到银行存了一笔三年期的定期存款，年利率是4.25%，若到期后取出得到本息和(本金+利息)33825元．设王先生存入的本金为x元，则下面所列方程正确的是（）

A、x+3×4.25%x=33 825 B、x+4.25%x=33 825 C、3×4.25%x=33825 D、3(x+4.25%x)=33 825

查看试题解析
8. 幻方是相当古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫图.将数字1，2，3，4，5，6，7，8，9分别填入如图所示的幻方中，要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15，则 $m$ 的值为（    ）



   3

   8

   5

   m

A、6 B、2 C、1 D、4

查看试题解析
9. 如图，大长方形是由5个完全相同的小长方形和一个边长为 $1.5 c m$ 的正方形拼成，则大长方形的面积是（）

A、 $2.25 c m^{2}$ B、 $4 c m^{2}$ C、 $6 c m^{2}$ D、 $10 c m^{2}$

查看试题解析
10. 如图，每个圆纸片的面积都是30，圆纸片A与B，B与C，C与A的重叠面积分别为6，8，5，三个圆纸片覆盖的总面积为73，则图中阴影部分的面积为（）

A、54 B、56 C、58 D、69

查看试题解析

二、填空题

11. 根据“ $x$ 的2倍与3的和比 $x$ 的二分之一少4”可列方程：.

查看试题解析
12. $A$ ， $B$ 两地相距 $450$ 千米，甲、乙两车分别从 $A$ ， $B$ 两地同时出发，相向而行，已知甲速度为 $120$ 千米/时，乙速度为 $80$ 千米/时， $t$ 小时后两车相距 $50$ 千米， $t$ 满足的方程是.

查看试题解析
13. 某种商品的标价为200元，为了吸引顾客，按九折出售，这时仍要盈利20%，则这种商品的进价是元．

查看试题解析
14. 小云的爸爸现在的年龄比小云大25岁，5年后小云爸爸的年龄是小云的2倍少10岁，小云现在岁.

查看试题解析
15. 阳光小学组织安全意识知识竞赛，共 $20$ 题，评分规则是答对一题得 $10$ 分，答错一题扣 $5$ 分，弃权不扣分也不得分，芳芳小组弃权两题，得了 $120$ 分，他们答对了题 $.$

查看试题解析

16. 下表是某市居民出行方式以及收费标准：（不足1千米按1千米算）

打车方式	出租车	3千米以内8元；超过3千米的部分2.4元/千米
打车方式	滴滴快车	路程：1.4元/千米；时间：0.6元/分钟
说明	打车的平均车速40千米/时

假设乘坐8千米，耗时：8÷40×60＝12分钟；出租车收费：8＋（8－3）×2.4＝20元；滴滴快车收费：8×1.4＋12×0.6＝18.4元．

为了提升市场竞争力，出租车公司推出行使里程超过10千米立减4.8元活动．小聪乘坐出租车从甲地到达乙地支付车费22.4元，若改乘滴滴快车从甲地到乙地，则需支付元．

查看试题解析

三、解答题

17. 用方程解答：x的3倍与1之和的二分之一等于x的四倍与1之差的三分之一，求x．

查看试题解析
18. 为庆祝“建党100周年”，某学校组织“学党史”知识竞赛，共设20道选择题，每题必答，答对1题得5分，答错1题扣1分，参赛者小红得88分，则她答对几道题？

查看试题解析
19. 某车间有28名工人，生产一种螺栓和螺帽，平均每人每小时能生产螺栓12个或螺帽18个，一个螺栓配两个螺帽，应分配多少人生产螺栓，多少人生产螺帽，才能使生产的螺栓和螺帽刚好配套？

查看试题解析
20. 植树节，小明种树棵数是小聪种树棵数的1.2倍，小慧种树棵数是小明种树棵数的一半少5棵，三人一共种树23棵.设小聪种了x棵树.

(1)、小明种树棵，小慧种树棵（用含x的代数式表示）.

(2)、请求出小聪种树的棵树.

查看试题解析
21. 一列匀速前进的火车，通过列车隧道.

(1)、如果通过一个长300米的隧道AB，从车头进入隧道到车尾离开隧道，共用15秒的时间（如图1），又知其间在隧道顶部的一盏固定的灯发出的一束光垂直照射火车2.5秒，求这列火车的长度；

图一

(2)、如果火车以相同的速度通过了另一个隧道CD，从火车车尾全部进入隧道到火车车头刚好到达隧道出口（如图2），其间共用20秒时间，求这个隧道CD的长.

图二

查看试题解析

22. 一家电信公司推出手机话费套餐活动，具体资费标准见下表：

套餐月租费（元/月）	套餐内容		套餐外资费
套餐月租费（元/月）	主叫限定时间（分钟）	被叫	主叫超时费（元/分钟）
58	50	免费	0.25
88	150		0.20
118	350		0.15
说明：①主叫：主动打电话给别人；被叫：接听别人打进来的电话 ②若办理的是月租费为58元的套餐，主叫时间不超过50分钟时，当月话费即为58元；若主叫时间为60分钟，则当月话费为58+0.25×(60-50)=60.5元．其他套餐计费方法类似

(1)、已知小聪办理的是月租费为88元的套餐，小明办理的是月租费为118元的套餐，他们某个月的主叫时间都为m分钟(m> 360)．

①请用含m的代数式分别表示该月他们的话费，化简后填空：小聪该月的话费为 ▲ 元；小明该月的话费为 ▲ 元．

②若该月小聪比小明的话费还要多14元，求他们的通话时间．

(2)、若小慧的两个手机号码分别办理了58元、88元套餐．该月她的两个号码主叫时间共为220分钟，总话费为152元，求她两个号的主叫时间分别可能是多少分钟．

查看试题解析

23. 小明在学习了正方体的展开图后，明白了很多几何体都能展开成平面图形．于是他在家用剪刀剪开了一个长方体纸盒，可是一不小心多剪开了一条棱，把纸盒剪成了两部分，如图1、图2所示．请根据你所学的知识，回答下类问题：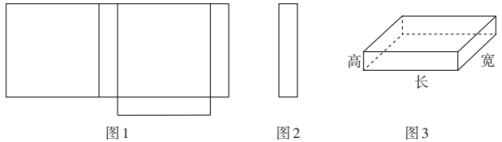
观察判断：
小明共剪开了 ▲ 条棱；
动手操作：
现在小明想将剪断的图2重新粘贴到图1上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒（如图3），请你帮助小明在图1中补全图形：
解决问题：
经过测量，小明发现这个纸盒的底面是一个正方形，其边长是长方体的高的5倍，并且纸盒所有棱长的和是 $880 c m$ ，求这个纸盒的体积．

查看试题解析