（第一次学期同步） 5.3一元一次方程的解法—2023-2024学年浙教版七年级数学

试卷更新日期：2023-11-30 类型：同步测试

进入出卷网下载

一、选择题

1. 解方程1-2(2x-1)=x，以下去括号正确的是（）

A、1-4x-2=x B、1-4x+1=x C、1-4x+2=x D、1-4x+2=-x

查看试题解析
2. 下列解方程的过程中，移项错误的是（）

A、方程2x+6=-3变形为2x=-6+3 B、方程2x-6=-3变形为2x=-3+6 C、方程3x=4-x变形为3x+x=4 D、方程4-x=3x变形为x+3x=4

查看试题解析
3. 一元一次方程x+1=3的解是（）

A、x=2 B、x=-2 C、x=4 D、x=-4

查看试题解析
4. 解方程 $2 (x + 1) - 3 (x - 1) = 6$ 的步骤如图所示，则在每一步变形中，依据“等式的基本性质”有（）

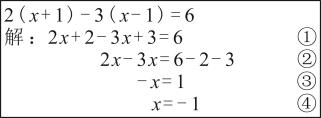A、①② B、②③ C、③④ D、②④

查看试题解析
5. 冉冉解方程 $- 3 (★ - 9) = 5 x - 1$ 时，发现★处一个常数被涂抹了，已知方程的解是 $x = 5$ ，则★处的数字是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 解方程 $\frac{2 x - 1}{3} - \frac{3 x - 4}{4} = 1$ 时，去分母正确的是（）

A、4（2x-1）-9x-12=1 B、8x-4-3（3x-4）=12 C、4（2x-1）-9x+12=1 D、8x-4+3（3x-4）=12

查看试题解析
7. 已知 $x = 1$ 是关于x的一元一次方程 $2 x - a = 0$ 的解，则a的值为（）

A、 $- 1$ B、 $- 2$ C、1 D、2

查看试题解析
8. 若关于 $x$ 的方程 $k x - 2 x = 14$ 的解是正整数，则 $k$ 的整数值有个．（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 若单项式 $\frac{1}{3} a^{m + 1} b^{3}$ 与 $- 2 a^{3} b^{n}$ 的和仍是单项式，则方程 $\frac{x - 7}{n} - \frac{1 + x}{m} = 1$ 的解为（）

A、 $x = - 23$ B、 $x = 23$ C、 $x = - 29$ D、 $x = 29$

查看试题解析
10. 阅读：关于x方程ax=b在不同的条件下解的情况如下：（1）当a≠0时，有唯一解x= $\frac{b}{a}$ ；（2）当a=0，b=0时有无数解；（3）当a=0，b≠0时无解．请你根据以上知识作答：已知关于x的方程 $\frac{x}{3}$ a= $\frac{x}{2}$ ﹣ $\frac{1}{6}$ （x﹣6）无解，则a的值是（）

A、1 B、﹣1 C、±1 D、a≠1

查看试题解析

二、填空题

11. 方程 $4 x = 3 x - 4$ 的解是 $x =$ ．

查看试题解析
12. 如果 $\frac{1}{3} - x = 5$ ，那么 $1 - 3 x =$

查看试题解析
13. 若关于x的方程5x﹣1＝2x+a的解与方程4x+3＝7的解互为相反数，则a＝.

查看试题解析
14. 若m、n互为相反数，且 $m \neq 0$ ，那么关于x的方程 $m x - n = 0$ 的解为；

查看试题解析
15. 如图是一个数表，现用一个矩形在数表中任意框出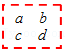4个数，当a+b+c+d＝32时，a＝．

查看试题解析
16. 如表，有 $12$ 个方格，每个方格内都有一个数，若任何相邻三个数的和都是 $18$ ，则 $x$ 的值是．
     $5$
     $A$
     $B$
     $C$
     $D$
     $E$
     $F$
     $x$
     $G$
     $H$
     $P$
          $10$

查看试题解析

三、解答题

17. 解方程．

(1)、 $\frac{2}{3} x \div \frac{1}{4} = 24$

(2)、 $50 % + \frac{1}{3} x = 20$

查看试题解析
18. 当m取何值时，代数式 $\frac{m + 1}{3}$ 的值比 $\frac{3 m + 1}{2}$ 的值小1？

查看试题解析
19. 某同学解方程 $\frac{10 - x}{4} = 1 - \frac{x - y}{3}$ ，在去分母时，忘记把1乘最小公分母，结果求得的解为x=-1，现请你帮他求出正确的解．

查看试题解析
20. 如果两个方程的解相差1，则称解较大的方程为另一个方程的“后移方程”.
例如：方程 $x - 2 = 0$ 是方程 $x - 1 = 0$ 的后移方程.

(1)、判断方程 $2 x + 1 = 0$ 是否为方程 $2 x + 3 = 0$ 的后移方程（填“是”或“否”）；

(2)、若关于x的方程 $3 x + m = 0$ 是关于x的方程 $2 (x - 2) = - 4 (3 + x)$ 的后移方程，求m的值.

查看试题解析
21. 已知(a-1)x²-3(x-1)+m=0是关于x的一元一次方程．

(1)、求a的值．

(2)、若上述方程的解比关于x的方程3x-2m=2x-4的解大2，求m的值．

查看试题解析
22. 数学家欧拉最先把关于x的多项式用记号f（x）来表示.例如：f（x）＝x²+x-1，当x＝a时.多项式的值用f（a）来表示，即f（a）＝a²+a-1.当x＝3时，f（3）＝3²+3-1＝11.

(1)、已知f（x）＝x²-2x+3，求f（1）的值.

(2)、已知f（x）＝mx²-2x-m，当f（-3）＝m-1时，求m的值.

(3)、已知f（x）＝kx²-ax-bk（a.b为常数），对于任意有理数k，总有f（-2）＝-2，求a，b的值.

查看试题解析
23. 定义：如果两个一元一次方程的解之和为1，我们就称这两个方程为“美好方程”.例如：方程 $2 x - 1 = 3$ 和 $x + 1 = 0$ 为“美好方程”.

(1)、方程 $4 x - (x + 5) = 1$ 与方程 $- 2 y - y = 3$ 是“美好方程”吗？请说明理由；

(2)、若关于x的方程 $\frac{x}{2} + m = 0$ 与方程 $3 x - 2 = x + 4$ 是“美好方程”，求m的值；

(3)、若关于x方程 $2 x - n + 3 = 0$ 与 $x + 5 n - 1 = 0$ 是“美好方程”，求n的值.

查看试题解析