（第一次学期同步） 5.2等式的基本性质—2023-2024学年浙教版七年级数学

试卷更新日期：2023-11-30 类型：同步测试

进入出卷网下载

一、选择题

1. 已知等式3a=2b+5，则下列等式中，不一定成立的是（）

A、3a+1=2b+6 B、3a-5=2b C、a= $\frac{2}{3} b + \frac{5}{3}$ D、3= $\frac{2 b}{a} + \frac{5}{a}$

查看试题解析
2. 下列运用等式的性质对等式进行的变形中，不正确的是（）

A、若 $x = y$ ，则 $x - y = 0$ B、若 $a = b$ ，则 $a c = b c$ C、若 $\frac{a}{c} = \frac{b}{c}$ ，则 $a = b$ D、若 $x = y$ ，则 $\frac{x}{y} = 1$

查看试题解析
3. 下列等式不一定成立的是（）

A、若 $a c = b c$ ，则 $a = b$ B、若 $\frac{a}{c} = \frac{b}{c}$ ，则 $a = b$ C、若 $- a = - b$ ，则 $2 - a = 2 - b$ D、若 $(x^{2} + 1) a = (x^{2} + 1) b$ ，则 $a = b$

查看试题解析
4. 方程2x-4=3x+8经移项，可得2x-3x=8+4．这实际上是根据等式的性质，在方程的两边都加上（）

A、-3x+4 B、3x-4 C、-3x-4 D、3x+4

查看试题解析
5. 下列各式中，变形正确的是（）

A、若 $a = b$ ，则 $a + c = b + c$ B、若 $2 x = a$ ，则 $x = a - 2$ C、若 $6 a = 2 b$ ，则 $a = 3 b$ D、若 $a = b + 2$ ，则 $3 a = 3 b + 2$

查看试题解析
6. 等式就像平衡的天平，能与如图的事实具有相同性质的是（）

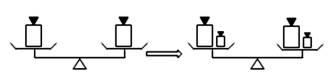A、如果 $a = b$ ，那么 $a c = b c$ B、如果 $a = b$ ，那么 $\frac{a}{c} = \frac{b}{c} (c \neq 0)$ C、如果 $a = b$ ，那么 $a + c = b + c$ D、如果 $a = b$ ，那么 $a^{2} = b^{2}$

查看试题解析
7. 解方程， $1 - \frac{x + 3}{6} = \frac{x}{2}$ 利用等式性质去分母正确的是（）

A、 $1 - x - 3 = 3 x$ B、 $6 - x - 3 = 3 x$ C、 $6 - x + 3 = 3 x$ D、 $1 - x + 3 = 3 x$

查看试题解析
8. 将方程 $\frac{2 x - 1}{2} - \frac{x + 1}{3} = 1$ 去分母后，得到3(2x-1)- 2x+1=6的结果错在（）

A、最简公分母找错 B、去分母时漏乘3项 C、去分母时分子部分没有加括号 D、去分母时各项所乘的数不同

查看试题解析
9. 若 $x = 3 t + 1 ， y = 2 t - 1$ ，用含y的式子表示x的结果是（）

A、 $y = \frac{2 x - 5}{3}$ B、 $x = \frac{3 y + 5}{2}$ C、 $y = \frac{2 x + 5}{3}$ D、 $x = \frac{3 y - 5}{2}$

查看试题解析
10. 下列各对等式，是根据等式的性质进行变形的，其中错误的是（）．

A、4x-1=5x+2→x=-3 B、 $\frac{x}{0.5} - \frac{1.8 - 2 x}{0.7} = 23 \to \frac{10 x}{5} - \frac{18 - 20 x}{7} = 230$ C、 $\frac{0.03 x}{2} + \frac{0.05 - 0.1 x}{4} = 0.23 \to \frac{3}{2} x + \frac{5 - 10 x}{4} = 23$ D、 $\frac{x + 5}{3} - \frac{x - 3}{2} = 1 \to 2 (x + 5) - 3 (x - 3) = 6$

查看试题解析

二、填空题

11. 由3x+5=10，得到3x=10-5的依据是.

查看试题解析
12. 当 $x = 2$ 时，代数式 $a x - 2$ 的值为6，则 $a$ 的值是.

查看试题解析
13. 已知 $2 x^{m - 1}$ +4=0是一元一次方程，则m=.

查看试题解析
14. 当 $a =$ 时， $4 a - 5$ 与 $5 a - 4$ 的值互为相反数.

查看试题解析
15. 已知：如图，这是一种数值转换机的运算程序．存在输入的数x，使第2次输出的数还是x，直接写出所有符合条件x的值．

查看试题解析
16. 我们规定能使等式 $\frac{m}{2} + \frac{n}{4} = \frac{m + n}{2 + 4}$ 成立的一对数（m，n）为“好友数对”.例如当m=2，n=-8 时，能使等式成立，则（2，﹣8）是“好友数对”.若（a，6）是“好友数对”，则a＝.

查看试题解析

三、解答题

17. 解下列方程：

(1)、5x-9=-3x+ 7；

(2)、 $\frac{2 x - 1}{3} = \frac{x + 2}{2} - 2$

查看试题解析
18. 利用等式基本性质，把5+ $\frac{2}{7}$ x=9﹣ $\frac{4}{7}$ y中的x用关于y的代数式表示，再将等式中的y用关于x的代数式表示．

查看试题解析
19. 已知 $\frac{3}{4}$ m﹣1= $\frac{3}{4}$ n，试用等式的性质比较m与n的大小．

查看试题解析
20. 等式(k-2)x²+kx+1=0是关于x的一元一次方程(即x未知),求这个方程的解.

查看试题解析
21. 已知方程 $4 x + 2 m = 3 x + 1$ 和方程 $3 x + 2 m = 6 x + 1$ 的解相同.

(1)、求m的值；

(2)、求代数式 ${(- 2 m)}^{2020} - {(m - \frac{3}{2})}^{2021}$ 的值.

查看试题解析
22. 在数学课上，老师给出了一道题目：“先化简再求值： $(x^{2} + □ x - 1) - 3 (\frac{1}{3} x^{2} - 2 x + 4)$ ，其中 $x = - 1$ ”， $□$ 中的数据被污染，无法解答，只记得 $□$ 中是一个实数，于是老师即兴出题，请同学们回答.

(1)、化简后的代数式中常数项是多少？

(2)、若点点同学把“ $x = - 1$ ”看成了“ $x = 1$ ”，化简求值的结果仍不变，求此时 $□$ 中数的值；

(3)、若圆圆同学把“ $x = - 1$ ”看成了“ $x = 1$ ”，化简求值的结果为-3，求当 $x = - 1$ 时，正确的代数式的值.

查看试题解析
23. 如图，已知数轴上点A表示的数为8，B是数轴上一点，且AB=14．动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．

(1)、写出数轴上点B表示的数，点P表示的数（用含t的代数式表示）；

(2)、动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？

(3)、若点D是数轴上一点，点D表示的数是x，请你探索式子 $| x + 6 | + | x - 8 |$ 是否有最小值？如果有，直接写出最小值；如果没有，说明理由．

查看试题解析