备战2024学年中考数学细点逐一突破真题训练第12章全等三角形
试卷更新日期:2023-11-30 类型:一轮复习
一、一线三等角型
-
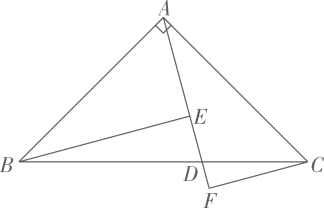
1. 如图,在中, , , 点D为上一点,连接 . 过点B作于点E,过点C作交的延长线于点F.若 , , 则的长度为 .
 2. 如图,是边长为4的等边三角形,点D,E,F分别在边 , , 上运动,满足 .
2. 如图,是边长为4的等边三角形,点D,E,F分别在边 , , 上运动,满足 . (1)、求证:;(2)、设的长为x,的面积为y,求y关于x的函数解析式;(3)、结合(2)所得的函数,描述的面积随的增大如何变化.3.
(1)、求证:;(2)、设的长为x,的面积为y,求y关于x的函数解析式;(3)、结合(2)所得的函数,描述的面积随的增大如何变化.3.

 (1)、操作思考:如图1,在平面直角坐标系中,等腰的直角顶点在原点,若顶点A恰好落在点处,则点的坐标为 .(2)、感悟应用:如图2,一次函数的图像与轴交于点A , 与轴交于点 , 过点作线段且 , 直线交轴于点D .
(1)、操作思考:如图1,在平面直角坐标系中,等腰的直角顶点在原点,若顶点A恰好落在点处,则点的坐标为 .(2)、感悟应用:如图2,一次函数的图像与轴交于点A , 与轴交于点 , 过点作线段且 , 直线交轴于点D .①点A的坐标为 , 点B的坐标为;
②直接写出点C的坐标;
(3)、拓展研究:如图3,在平面直角坐标系中,的顶点分别在轴、轴上,且 , , 若点的坐标为 , 点A的坐标为 , 点在第四象限,请求出点的坐标.4. 如图1,点P是线段AB上与点A,点B不重合的任意一点,在AB的同侧分别以A,P,B为顶点作 ∠1=∠2=∠3,其中∠1与∠3的一边分别是射线AB和射线BA,∠2的两边不在直线AB上,我们规定这三个角互为等联角,点P为等联点,线段AB为等联线.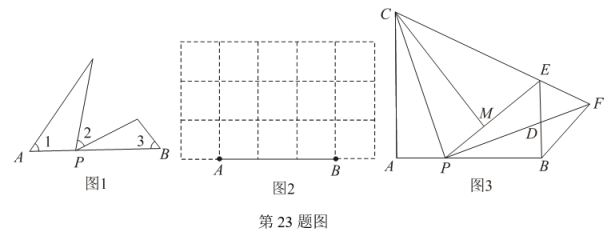 (1)、如图2,在5×3个方格的纸上,小正方形的顶点为格点、边长均为1,AB为端点在格点的已知线段.请用三种不同连接格点的方法,作出以线段AB为等联线、某格点P为等联点的等联角,并标出等联角,保留作图痕迹;(2)、如图3,在Rt△APC中,∠A=90°, , 延长AP至点B,使AB=AC,作∠A的等联角∠CPD和∠PBD.将△APC沿PC折叠,使点A落在点M处,得到△MPC,再延长PM交BD的延长线于E,连接CE并延长交PD的延长线于F,连接BF.
(1)、如图2,在5×3个方格的纸上,小正方形的顶点为格点、边长均为1,AB为端点在格点的已知线段.请用三种不同连接格点的方法,作出以线段AB为等联线、某格点P为等联点的等联角,并标出等联角,保留作图痕迹;(2)、如图3,在Rt△APC中,∠A=90°, , 延长AP至点B,使AB=AC,作∠A的等联角∠CPD和∠PBD.将△APC沿PC折叠,使点A落在点M处,得到△MPC,再延长PM交BD的延长线于E,连接CE并延长交PD的延长线于F,连接BF.①确定△PCF的形状,并说明理由;
②若AP:PB=1:2,BF=k,求等联线AB和线段PE的长(用含k的式子表示).
二、手拉手模型
-
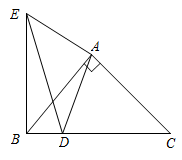
5. 如图,在中, , , . 点在上,且 . 连接 , 将线段绕点顺时针旋转得到线段 , 连接 , . 则的面积是( )
 A、 B、 C、 D、6. 如图,在中, , , 以为边在下方作 , 连接 , 已知 , , 则的最大值为 .
A、 B、 C、 D、6. 如图,在中, , , 以为边在下方作 , 连接 , 已知 , , 则的最大值为 .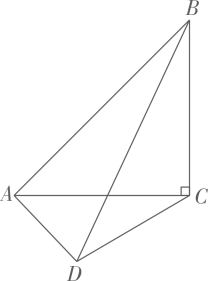 7. 【问题呈现】
7. 【问题呈现】和都是直角三角形, , 连接 , , 探究 , 的位置关系.
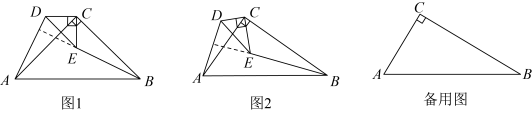 (1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】
(1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】当时,将绕点C旋转,使三点恰好在同一直线上,求的长.
8. 已知和都是等边三角形,分别连接 . (1)、如图1,若 .
(1)、如图1,若 .①求的度数;
②延长交于点F , 求证:;
(2)、如图2,若点D在边上,延长交于点G , 连接 . 求证:平分 .9.(1)、【问题呈现】如图1,和都是等边三角形,连接 . 求证: .
 (2)、【类比探究】
(2)、【类比探究】如图2,和都是等腰直角三角形, . 连接 . 请直接写出的值.
(3)、【拓展提升】如图3,和都是直角三角形, , 且 . 连接 . 延长交于点F,交于点G.求的值.
三、倍长中线型
-
10. “倍长中线法”是解决几何问题的重要方法.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,具体做法是:如图,是的中线,延长到 , 使 , 连接 , 构造出和 . 求证: .
 11. 如图,在中, , 是斜边上的中点,、分别是、边上的点,且
11. 如图,在中, , 是斜边上的中点,、分别是、边上的点,且 (1)、若 , , 求四边形的面积.(2)、求证:.12. 综合与实践
(1)、若 , , 求四边形的面积.(2)、求证:.12. 综合与实践小明遇到这样一个问题,如图1,中, , , 点D为的中点,求的取值范围.
小明发现老师讲过的“倍长中线法”可以解决这个问题,所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法,他的做法是:如图2,延长到E,使 , 连接 , 构造 , 经过推理和计算使问题得到解决
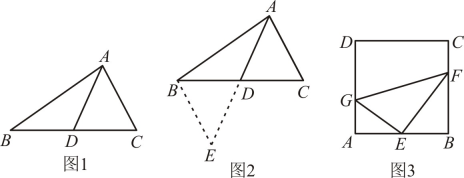
请回答:
(1)、小明证明用到的判定定理是:____;(填入你选择的选项字母)A、 B、 C、 D、(2)、的取值范围是.(3)、小明还发现:倍长中线法最重要的一点就是延长中线一倍,完成全等三角形模型的构造.
参考小明思考问题的方法,解决问题:
如图3,在正方形中,E为边的中点,G、F分别为 , 边上的点,若 , , , 求的长.13. 在中, , F是的中点,作于点E,垂足E在线段上(不与A、B重合),连接、 . (1)、如图1,若 , 求的度数;(2)、求证:;(3)、如图2,若E为的中点,请直接写出与的关系.14. 在等腰直角中, , , 将直角边AC绕点A顺时针旋转得到AP,旋转角为 , 连接CP,PB.
(1)、如图1,若 , 求的度数;(2)、求证:;(3)、如图2,若E为的中点,请直接写出与的关系.14. 在等腰直角中, , , 将直角边AC绕点A顺时针旋转得到AP,旋转角为 , 连接CP,PB.

 (1)、如图1,当时,求BP的长;(2)、如图2,若 , 且D为AB中点,连接PD,猜想CP和DP的数量关系,并说明理由;(3)、在旋转过程中,当时,求旋转角的度数.
(1)、如图1,当时,求BP的长;(2)、如图2,若 , 且D为AB中点,连接PD,猜想CP和DP的数量关系,并说明理由;(3)、在旋转过程中,当时,求旋转角的度数.四、半角模型(45°,60°,120°)
-
15. 如图,在正方形中,点 , 分别在 , 上,连接 , , , . 若 , 则一定等于( )
 A、 B、 C、 D、16.
A、 B、 C、 D、16.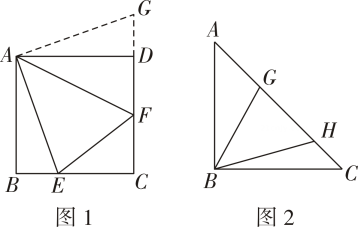 (1)、建立模型:如图 , 在正方形中, , 分别是 , 上的点,且 , 探究图中线段 , , 之间的数量关系小王同学探究此问题的方法是将绕点逆时针旋转使得与重合,连接 , 由此得到 ,再证明≌ ,可得出线段 , , 之间的数量关系为 .(2)、拓展延伸:如图 , 在等腰直角三角形中, , , 点 , 在边上,且 , 写出图中线段 , , 之间的数量关系并证明.17.(1)、如图①,在正方形中,E,F分别是 , 边上的动点,且 , 将绕点D逆时针旋转90°,得到 , 可以证明 , 进一步推出 , , 之间的数量关系为;
(1)、建立模型:如图 , 在正方形中, , 分别是 , 上的点,且 , 探究图中线段 , , 之间的数量关系小王同学探究此问题的方法是将绕点逆时针旋转使得与重合,连接 , 由此得到 ,再证明≌ ,可得出线段 , , 之间的数量关系为 .(2)、拓展延伸:如图 , 在等腰直角三角形中, , , 点 , 在边上,且 , 写出图中线段 , , 之间的数量关系并证明.17.(1)、如图①,在正方形中,E,F分别是 , 边上的动点,且 , 将绕点D逆时针旋转90°,得到 , 可以证明 , 进一步推出 , , 之间的数量关系为;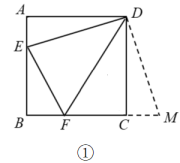 (2)、在图①中,连接分别交和于P,Q两点, 求证:;(3)、如图②,在菱形中, , 点E,F分别是边 , 上的动点(不与端点重合),且 , 连接分别与边 , 交于M,N.当时,猜想 , , 之间存在什么样的数量关系,并证明你的结论.
(2)、在图①中,连接分别交和于P,Q两点, 求证:;(3)、如图②,在菱形中, , 点E,F分别是边 , 上的动点(不与端点重合),且 , 连接分别与边 , 交于M,N.当时,猜想 , , 之间存在什么样的数量关系,并证明你的结论.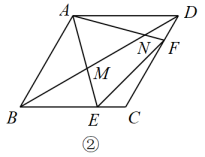
五、截长补短模型
-
18. 如图,在中, , , 过点作 , 且 , 过点作交于点 , 连接 .
 (1)、如图1,若 , 且 , 求的度数;(2)、如图2,若 , 求证: .19. 如图,四边形是正方形,M是边上的一点,E是的中点,平分 .
(1)、如图1,若 , 且 , 求的度数;(2)、如图2,若 , 求证: .19. 如图,四边形是正方形,M是边上的一点,E是的中点,平分 . (1)、判断与的数量关系,并说明理由;(2)、求证:;(3)、若 , 求的长.20.
(1)、判断与的数量关系,并说明理由;(2)、求证:;(3)、若 , 求的长.20.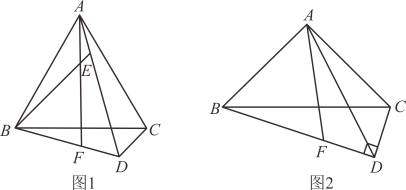 (1)、【模型建立】如图1,和都是等边三角形,点关于的对称点在边上.
(1)、【模型建立】如图1,和都是等边三角形,点关于的对称点在边上.①求证:;
②用等式写出线段 , , 的数量关系,并说明理由.
(2)、【模型应用】如图2,是直角三角形, , , 垂足为 , 点关于的对称点在边上.用等式写出线段 , , 的数量关系,并说明理由.
(3)、【模型迁移】在(2)的条件下,若 , , 求的值.
六、对角互补模型
-
21. 问题探究:
 (1)、如图1,中, , , 是高,求证:.(2)、如图2,在(1)条件下,、分别是和上的点,且 , 如果 , 那么四边形的面积是;(3)、如图3,四边形中,平分 , , , , 求的值.
(1)、如图1,中, , , 是高,求证:.(2)、如图2,在(1)条件下,、分别是和上的点,且 , 如果 , 那么四边形的面积是;(3)、如图3,四边形中,平分 , , , , 求的值.七、十字架模型
-
22. 如图:
 (1)、如图1,已知线段AD、EC相交于点F,连接AE、DC.若∠E=∠D=90°,
(1)、如图1,已知线段AD、EC相交于点F,连接AE、DC.若∠E=∠D=90°,求证:∠A=∠C;
(2)、如图2,△ABC中, AD⊥BC垂足为点D,CE⊥AB垂足为点E,∠BAC=45°.求证:BE=EF;
(3)、如图3,在(2)的前提下,若AB=AC,求的值.23. 如图,正方形中,点 , 分别在 , 上,且 , 与相交于点 . (1)、求证:≌;(2)、求的大小.24. 正方形中,点E为边上的任意一点(点E不与B,C重合),点P为线段上一动点,过点P作直线 .
(1)、求证:≌;(2)、求的大小.24. 正方形中,点E为边上的任意一点(点E不与B,C重合),点P为线段上一动点,过点P作直线 . (1)、如图1,当直线l经过点D时,直线l交边于点F,求证:;(2)、如图2,当直线l分别交边,边于点M,点N时,如果 , 求的长.25. 如图,正方形边长为4,点E在边上(点E与点A、B不重合),过点A作 , 垂足为G,与边相交于点F.
(1)、如图1,当直线l经过点D时,直线l交边于点F,求证:;(2)、如图2,当直线l分别交边,边于点M,点N时,如果 , 求的长.25. 如图,正方形边长为4,点E在边上(点E与点A、B不重合),过点A作 , 垂足为G,与边相交于点F.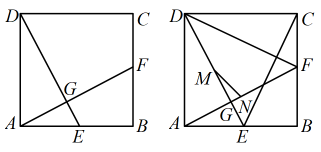 (1)、求证:;(2)、若的面积为 , 求的长;(3)、在(2)的条件下,取 , 的中点M,N,连接 , 求的长.26. 如图,正方形的边长为 , E,F分别是的中点,与分别交于点M,N. 请你回答下列问题:
(1)、求证:;(2)、若的面积为 , 求的长;(3)、在(2)的条件下,取 , 的中点M,N,连接 , 求的长.26. 如图,正方形的边长为 , E,F分别是的中点,与分别交于点M,N. 请你回答下列问题: (1)、求证:.(2)、直接写出的长.(3)、求的面积.
(1)、求证:.(2)、直接写出的长.(3)、求的面积.八、角平分线模型
-
27. 如图,在中, , 以为圆心,任意长为半径画弧,分别交 , 于点 , , 再分别以 , 为圆心,大于的定长为半径画弧,两弧交于点 , 作射线交于点 , 作 , 垂足为 , 则下列结论不正确的是( )
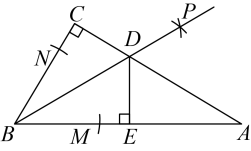 A、 B、 C、 D、一定经过的内心28. 如图,在中, , D为上一点,若是的角平分线,则 .
A、 B、 C、 D、一定经过的内心28. 如图,在中, , D为上一点,若是的角平分线,则 .
-

