（人教版）2024年中考数学一轮复习统计与概率--概率练习题

试卷更新日期：2023-11-29 类型：一轮复习

进入出卷网下载

一、选择题

1. 任意掷一枚质地均匀的骰子，正面朝上的点数为 $3$ 的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{6}$

查看试题解析
2. 如图，在 $3 \times 4$ 的网格中，其中有 $5$ 个小正方形被涂成了黑色，一个小球在此网格内自由滚动并随机地停留在某个小正方形上，它最终停留在黑色区域的概率是（）

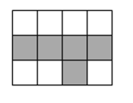A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{5}{12}$ D、 $\frac{7}{12}$

查看试题解析
3. 小颖、小明两人做游戏，掷一枚硬币，双方约定：正面朝上小颖胜，反面朝上小明胜，则这个游戏（）

A、公平 B、对小颖有利 C、对小明有利 D、无法确定

查看试题解析
4. 一个不透明的盒子内装中有除颜色外，其余完全相同的 $2$ 个红球， $2$ 个白球， $2$ 个黄球，小星将盒中小球搅匀后，每次从中随机摸出一球，记下颜色后放回盒中搅匀，再从中随机摸出一球下面是他前两次摸球的情况：当小星第三次摸球时，下列说法正确的是（）

次数

第 $1$ 次

第 $2$ 次

第 $3$ 次

颜色

红球

红球

？

A、一定摸到红球 B、摸到红球的可能性小
C、一定摸不到红球 D、摸到红球、白球、黄球的可能性一样大

查看试题解析
5. 不透明的袋子中装有一个红色小球和一个白色小球，除颜色外两个小球无其他差别 $.$ 从中随机取出一个小球后，放回并摇匀，再从中随机取出一个小球，则两次都取到白色小球的概率为（）

A、 $\frac{3}{4}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
6. 如图 $1$ ，一个均匀的转盘被平均分成 $10$ 等份，分别标有 $1$ ， $2$ ， $3$ ， $4$ ， $5$ ， $6$ ， $7$ ， $8$ ， $9$ ， $10 .$ 小凯转动转盘做频率估计概率的实验，当转盘停止转动后，指针指向的数字即为实验转出的数字，图 $2$ ，是小凯记录下的实验结果情况，那么小凯记录的实验是（）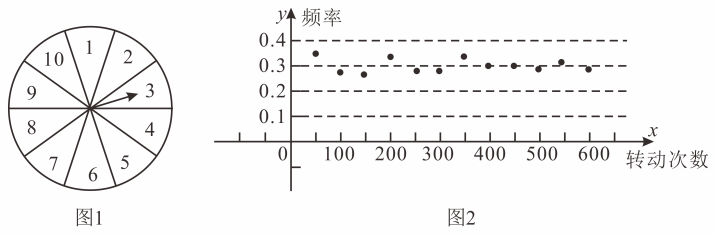

A、转动转盘后，出现偶数 B、转动转盘后，出现能被 $3$ 整除的数
C、转动转盘后，出现比 $6$ 大的数 D、转动转盘后，出现能被 $5$ 整除的数

查看试题解析
7. 下列事件中，是必然事件的是（）

A、任意画一个三角形，其内角和是 $18 0^{∘}$ B、任意买一张电影票，座位号是单号 C、掷一次骰子，向上一面的点数是3 D、射击运动员射击一次，命中靶心

查看试题解析
8. 1有7张扑克牌如图所示，将其打乱顺序后，背面朝上放在桌面上．若从中随机抽取一张，则抽到的花色可能性最大的是（）

A、 B、 C、 D、

查看试题解析
9. 掷两枚质地均匀的骰子，下列事件是随机事件的是（）

A、点数的和为1 B、点数的和为6 C、点数的和大于12 D、点数的和小于13

查看试题解析
10. 为贯彻教育部《大中小学劳动教育指导纲要（试行）》文件精神，某学校积极开设种植类劳动教育课.某班决定每位学生随机抽取一张卡片来确定自己的种植项目，老师提供6张背面完全相同的卡片，其中蔬菜类有4张，正面分别印有白菜、辣椒、豇豆、茄子图案；水果类有2张，正面分别印有草莓、西瓜图案，每个图案对应该种植项目. 把这6张卡片背面朝上洗匀，小明随机抽取一张，他恰好抽中水果类卡片的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析

二、填空题

11. 衢州飞往成都每天有2趟航班.小赵和小黄同一天从衢州飞往成都，如果他们可以选择其中任一航班，则他们选择同一航班的概率等于.

查看试题解析
12. 在一个不透明的口袋中装有红球和白球共 $12$ 个，这些球除颜色外都相同，将口袋中的球搅匀后，从中随机摸出 $1$ 个球，记下它的颜色后再放回口袋中，不断重复这一过程，共摸球 $200$ 次，发现有 $50$ 次摸到红球，则口袋中红球约有个 $.$

查看试题解析
13. 如图，飞镖游戏板中每一块小正方形的面积相等．任意投掷飞镖1次且击中游戏板，则击中阴影部分的概率是．

查看试题解析
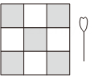14. 一个不透明的盒子中装有若干个红球和 $5$ 个黑球，这些球除颜色外均相同．经多次摸球试验后发现，摸到黑球的频率稳定在 $0.25$ 左右，则盒子中红球的个数约为．

查看试题解析
15. 围棋起源于中国，棋子分黑白两色．一个不透明的盒子中装有3个黑色棋子和若干个白色棋子，每个棋子除颜色外都相同，任意摸出一个棋子，摸到黑色棋子的概率是 $\frac{1}{4}$ ，则盒子中棋子的总个数是．

查看试题解析

三、解答题

16. 用如图所示的两个转盘（分别进行四等分和三等分），设计一个“配紫色”的游戏，分别转动两个转盘（指针指向区域分界线时，忽略不计），若其中一个转出红色，另一个转出蓝色即可配成紫色，求可配成紫色的概率．

查看试题解析
17. 一个不透明的布袋中装有标着数字2，3，6的三张卡片，从中任意抽取一张，用上面的数字做十位数，放回后，再抽取一张，用上面的数字做个位数，请用树状图或列表方法，求两次抽出的数字组成的数是4的倍数的概率.

查看试题解析
18. 某社区有1名男管理员和3名女管理员，现要从中随机选取2名管理员参与“社区防控"宣讲活动。请用画树状图或列表的方法求恰好选到“1男1女”的概率。

查看试题解析
19. 一个不透明的盒子中装有两个红球，一个白球和一个黄球，这些球除颜色外都相同，从中随机摸出一个球，记下颜色后不放回，再从中随机摸出一个球，请你用列表法或画树状图法求两次摸到的球的颜色都是红色的概率.

查看试题解析

四、综合题

20. 在一个不透明的盒子中装有 $4$ 个小球， $4$ 个小球上分别标有数字 $1$ ， $2$ ， $3$ ， $4$ ，这些小球除数字外其余都相同，现将小球搅拌均匀．

(1)、从盒子中任意抽取一个小球，恰好摸到标有奇数数字小球的概率是多少？

(2)、先从盒子中任意摸一个小球，再从余下的 $3$ 个小球中任意摸一个小球，求摸到的 $2$ 个小球标有的数字之和大于 $4$ 的概率 $($ 请用树状图或列表的方法求解 $)$ ．

查看试题解析
21. 为“学习二十大，永远跟党走，奋进新征程”庆祝活动，某学校组织志愿者周末到社区进行学习宣讲，决定从 $A ， B ， C ， D$ 四名志愿者中通过抽签的方式确定两名志愿者参加．抽签规则：将四名志愿者的名字分别写在四张完全相同不透明卡片的正面，把四张卡片背面朝上，洗匀后放在桌面上，先从中随机抽取一张卡片，记下名字，再从剩余的三张卡片中随机抽取第二张，记下名字．

(1)、“ $B$ 志愿者被选中”是事件（填“随机”或“不可能”或“必然”）；

(2)、请你用列表法或画树状图法表示出这次抽签所有可能的结果，并求出 $C ， D$ 两名志愿者被选中的概率．

查看试题解析
22. 张洋所住小区的每栋楼下均设有供业主使用的公共底面停车场，这天他放学回家时观察到位于他家楼下的停车场还剩余四个车位，小区规定每辆汽车停放时只能占用一个车位．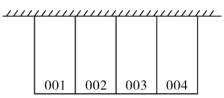

(1)、若此时有一辆汽车停车，则这辆车停在“003”号车位的概率是；

(2)、若此时有两辆汽车同时停车，求这两辆车停在相邻车位的概率．

查看试题解析
23. 今年2～4月某市出现了400名新冠肺炎患者，市委根据党中央的决定，对患者进行了免费治疗，图1是该市轻症、重症、危重症三类患者的人数分布统计图（不完整），图2是这三类患者的人均治疗费用统计图．请回答下列问题．

(1)、轻症患者的人数是多少？

(2)、所有患者的平均治疗费用是多少万元？

(3)、由于部分轻症患者康复出院，为减少病房拥挤，拟对某病房中的 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 五位患者任选两位转入另一病房，请用树状图法或列表法求出恰好选中 $B$ 、 $D$ 两位患者的概率．

查看试题解析

次数	第 $1$ 次	第 $2$ 次	第 $3$ 次
颜色	红球	红球	？

（人教版）2024年中考数学一轮复习 统计与概率--概率 练习题

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2024年中考数学一轮复习统计与概率--概率练习题