【北师大版·数学】2024年中考一轮复习之一元一次方程的实际应用-销售问题

试卷更新日期：2023-11-28 类型：一轮复习

进入 出卷网 下载

一、选择题

  • 1. 某商铺促销，单价80元的衬衫按照8折销售仍可获利10元，若这款衬衫的成本价为x元/件，则（ ）
    A、80×0.8-x＝10 B、（80-x）0.8-x＝10 C、80×0.8＝x-10 D、（80-x）×0.8＝x-10

    查看试题解析

  • 2. 根据如图中两人的对话纪录，求出哥哥买游戏机的预算为多少元？（   ）

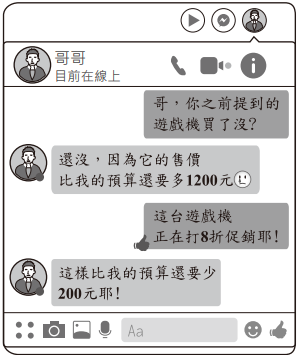    A、3800 B、4800 C、5800 D、6800

    查看试题解析

  • 3. 一种商品，先提价20%，再降价10%，这时的价格是2160元．则该商品原来的价格是（  ）
    A、2400元 B、2200元 C、2000元 D、1800元

    查看试题解析

  • 4. 某种商品每件的标价是a元，按标价的八折销售时，仍可获利15%，则这种商品每件的进价为（       ）
    A、0.8×(1−15%)a元 B、0.8a1−15%元 C、0.8a1+15%元 D、0.8×(1+15%)a元

    查看试题解析

  • 5. 由于换季，商场准备对某商品打折出售，如果按原售价的七五折出售，将亏损25元，而按原售价的九折出售，将盈利20元，则该商品的原售价为（   ）
    A、230元 B、250元 C、270元 D、300元

    查看试题解析

  • 6. 某超市正在热销一种商品，其标价为每件12元，打8折销售后每件可获利2元，该商品每件的进价为（    ）
    A、7.6元 B、7.7元 C、7.8元 D、7.9元

    查看试题解析

  • 7. 某商店举办促销活动，促销的方法是将原价x元的衣服以 35 （x﹣10）元出售，则下列说法中，能正确表达该商店促销方法的是（   ）
    A、原价减去10元后再打6折 B、原价打6折后再减去10元 C、原价减去10元后再打4折 D、原价打4折后再减去10元

    查看试题解析

  • 8. 小军到水果店买水果，他身上带的钱恰好可以购买15个苹果或21个橙子，若小军先买了9个苹果，则他身上剩下的钱最多可买橙子（   ）.
    A、7个 B、8个 C、9个 D、10个

    查看试题解析

  • 9. 某种商品每件的标价是220元，按标价的八折销售时，仍可获利10%，则这种商品每件的进价为（    ）
    A、200元 B、160元 C、150元 D、180元

    查看试题解析

  • 10. 某商铺促销，单价80元的衬衫按照8折销售仍可获利10元，若这款衬衫的成本价为 x 元/件，则（   ）
    A、80×0.8−x=10 B、(80−x)0.8−x=10 C、80×0.8=x−10 D、(80−x)×0.8=x−10

    查看试题解析

二、填空题

  • 11. 某商品随季节变化降价出售，如果按标价降价10%，仍可盈利40元．如果降价后再九折出售，就要亏损14元，则这件商品的标价是 元．

    查看试题解析

  • 12. 为进一步改善生态环境，村委会决定在甲、乙、丙三座山上种植香樟和红枫.在实际购买时，香樟的价格比预算低20% ， 红枫的价格比预算高25% ， 香樟购买数量减少了6.25% ， 红枫购买数量与预算保持不变，结果所花费用恰好与预算费用相等，则实际购买香樟的总费用与实际购买红枫的总费用之比为.

    查看试题解析

  • 13. 一家商店在销售某种服装（每件的标价相同）时，按这种服装每件标价的8折销售20件的销售额，与按这种服装每件的标价降低27元销售25件的销售额相等，则这种服装每件的标价是 元．

    查看试题解析

  • 14. 请从以下两个小题中任选一题作答，若多选，则按第一题计分.

    （A）儿童节期间，文具商店搞促销活动，同时购买一个书包和一个文具盒可以打8折优惠，能比标价省13.2元，已知书包标价比文具盒标价的3倍少6元.那么设一个文具盒标价为x元，依据题意列方程得.
    （B）用科学记算器计算： 13×17−3×15≈（计算结果保留两位小数）. 8.16

    查看试题解析

  • 15. 某商品随季节变化降价出售，如果按标价降价10%，仍可盈利12元，如果降价后再九折出售，就要亏损24元，则这件商品的标价是元.

    查看试题解析

三、解答题

  • 16. 某古镇为发展旅游产业，吸引更多的游客前往游览，助力乡村振兴，决定在“五一”期间对团队*旅游实行门票特价优惠活动，价格如下表：                                                                                              

    购票人数m（人）

             10≤m≤50

             51≤m≤100

             m>100

    每人门票价（元）

    60

    50

    40

    *题中的团队人数均不少于10人

    现有甲、乙两个团队共102人，计划利用“五一”假期到该古镇旅游，其中甲团队不足50人，乙团队多于50人．

    (1)、如果两个团队分别购票，一共应付5580元，问甲、乙团队各有多少人？
    (2)、如果两个团队联合起来作为一个“大团队”购票，比两个团队各自购票节省的费用不少于1200元，问甲团队最少多少人？

    查看试题解析

  • 17.  小区便民超市分别用2000元和4800元购进若干箱纯牛奶和酸奶，已知此次购进的酸奶的数量是纯牛奶数量的1.5倍，且每箱酸奶的价格比每箱纯牛奶的价格贵30元．
    (1)、求此次购进纯牛奶的数量．
    (2)、在销售过程中，纯牛奶每箱售价是80元，很快售完；酸奶每箱按进价加价25%销售，售出一部分后，恰逢五一假期，商场搞促销活动，决定打九折出售剩余的酸奶，已知纯牛奶和酸奶全部售出后共获利2150元，求有多少箱酸奶打九折出售？

    查看试题解析

  • 18. 某商场举办促销活动，本次活动中的家电消费券单笔交易满600元立减60元（每次只能使用一张）.某品牌电饭煲按进价提高50%后标价，若按标价的八折销售，当某顾客购买该电饭煲时，使用一张家电消费券后，又付现金636元，求该电饭煲的进价.

    查看试题解析

四、综合题

  • 19. 李叔叔批发甲、乙两种蔬菜到菜市场去卖，已知甲、乙两种蔬菜的批发价和零售价如下表所示：                                                                                                                 

    品名

    甲蔬菜

    乙蔬菜

    批发价/（元/kg）

             4.8

             4

    零售价/（元/kg）

             7.2

             5.6

    (1)、若他批发甲、乙两种蔬菜共40kg花180元．求批发甲乙两种蔬菜各多少千克？（列方程或方程组求解）
    (2)、若他批发甲、乙两种蔬菜共80kg花m元，设批发甲种蔬菜nkg ， 求m与n的函数关系式；
    (3)、在（2）的条件下，全部卖完蔬菜后要保证利润不低于176元，至少批发甲种蔬菜多少千克？

    查看试题解析

  • 20. 某商场欲购进A和B两种家电，已知B种家电的进价比A种家电的进价每件多100元，经计算，用1万元购进A种家电的件数与用1.2万元购进B种家电的件数相同．请解答下列问题：
    (1)、这两种家电每件的进价分别是多少元？
    (2)、若该商场欲购进两种家电共100件，总金额不超过53500元，且A种家电不超过67件，则该商场有哪几种购买方案？
    (3)、在（2）的条件下，若A和B两种家电的售价分别是每件600元和750元，该商场从这100件中拿出两种家电共10件奖励优秀员工，其余家电全部售出后仍获利5050元，请直接写出这10件家电中B种家电的件数．

    查看试题解析

  • 21. 我国航天事业发展迅速，2023年5月30日9时31分，神舟十六号载人飞船成功发射，某玩具店抓住商机，先购进了1000件相关航天模型玩具进行试销，进价为50元/件．
    (1)、设每件玩具售价为x元，全部售完的利润为y元．求利润y（元）关于售价x（元/件）的函数表达式；
    (2)、当售价定为60元/件时，该玩具销售火爆，该店继续购进一批该种航天模型玩具，并从中拿出这两批玩具销售利润的20%用于支持某航模兴趣组开展活动，在成功销售完毕后，资助经费恰好10000元，请问该商店继续购进了多少件航天模型玩具？

    查看试题解析