【北师大版·数学】2024年中考一轮复习之全等三角形的判定
试卷更新日期:2023-11-28 类型:一轮复习
一、选择题
-
1. 有下列条件:①两条直角边对应相等;②斜边和一锐角对应相等;③斜边和一直角边对应相等;④直角边和一锐角对应相等.其中能判定两直角三角形全等的有( )A、1个 B、2个 C、3个 D、4个2. 如图, , ,要使 ,需添加一个条件,下列所给的条件及相应的判定定理不正确的是( )
 A、 B、 C、 D、3. 如图,工人师傅设计了一种测零件内径的卡钳,卡钳交叉点O为、的中点,只要量出的长度,就可以道该零件内径的长度.依据的数学基本事实是( )
A、 B、 C、 D、3. 如图,工人师傅设计了一种测零件内径的卡钳,卡钳交叉点O为、的中点,只要量出的长度,就可以道该零件内径的长度.依据的数学基本事实是( )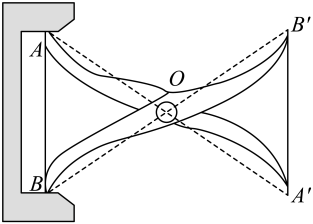 A、两边及其夹角分别相等的两个三角形全等 B、两角及其夹边分别相等的两个三角形全等 C、两余直线被一组平行线所截,所的对应线段成比例 D、两点之间线段最短4. 如图,在中,是中线,是角平分线,交延长线于点 , , , 则的长为( )
A、两边及其夹角分别相等的两个三角形全等 B、两角及其夹边分别相等的两个三角形全等 C、两余直线被一组平行线所截,所的对应线段成比例 D、两点之间线段最短4. 如图,在中,是中线,是角平分线,交延长线于点 , , , 则的长为( ) A、1.5 B、2 C、2.5 D、35. 如图,在中, , , , 点为边上的中点,交的延长线于点 , 交的延长线于点 , 且若 , 则的面积为( )
A、1.5 B、2 C、2.5 D、35. 如图,在中, , , , 点为边上的中点,交的延长线于点 , 交的延长线于点 , 且若 , 则的面积为( ) A、 B、 C、 D、6. 如图,正方形ABCD中,点F为AB上一点,CF与BD交于点E,连接AE,若∠BCF=20°,则∠AEF的度数( )
A、 B、 C、 D、6. 如图,正方形ABCD中,点F为AB上一点,CF与BD交于点E,连接AE,若∠BCF=20°,则∠AEF的度数( )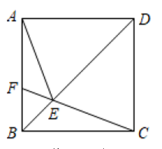 A、35° B、40° C、45° D、50°7. 阅读以下作图步骤:
A、35° B、40° C、45° D、50°7. 阅读以下作图步骤:①在和上分别截取 , 使;②分别以为圆心,以大于的长为半径作弧,两弧在内交于点;③作射线 , 连接 , 如图所示.根据以上作图,一定可以推得的结论是( )
 A、且 B、且 C、且 D、且8. 如图,在中, , 以为圆心,任意长为半径画弧,分别交 , 于点 , , 再分别以 , 为圆心,大于的定长为半径画弧,两弧交于点 , 作射线交于点 , 作 , 垂足为 , 则下列结论不正确的是( )
A、且 B、且 C、且 D、且8. 如图,在中, , 以为圆心,任意长为半径画弧,分别交 , 于点 , , 再分别以 , 为圆心,大于的定长为半径画弧,两弧交于点 , 作射线交于点 , 作 , 垂足为 , 则下列结论不正确的是( )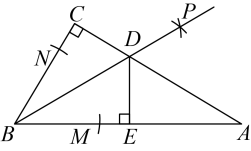 A、 B、 C、 D、一定经过的内心9. 要得知某一池塘两端A,B的距离,发现其无法直接测量,两同学提供了如下间接测量方案.
A、 B、 C、 D、一定经过的内心9. 要得知某一池塘两端A,B的距离,发现其无法直接测量,两同学提供了如下间接测量方案.方案Ⅰ:如图1,先过点B作 , 再在上取C,D两点,使 , 接着过点D作的垂线 , 交的延长线于点E,则测量的长即可;
方案Ⅱ:如图2,过点B作 , 再由点D观测,用测角仪在的延长线上取一点C,使 , 则测量的长即可.
对于方案Ⅰ、Ⅱ,说法正确的是( )
 A、只有方案Ⅰ可行 B、只有方案Ⅱ可行 C、方案Ⅰ和Ⅱ都可行 D、方案Ⅰ和Ⅱ都不可行10. 如图,锐角三角形ABC中, , 点D,E分别在边AB,AC上,连接BE,CD.下列命题中,假命题是( ).
A、只有方案Ⅰ可行 B、只有方案Ⅱ可行 C、方案Ⅰ和Ⅱ都可行 D、方案Ⅰ和Ⅱ都不可行10. 如图,锐角三角形ABC中, , 点D,E分别在边AB,AC上,连接BE,CD.下列命题中,假命题是( ). A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则二、填空题
-
11. 如图,在平面直角坐标系中,矩形的顶点A在x轴上,顶点C在y轴上,矩形的边在上, , 反比例函数的图象经过点B,若阴影部分面积为4,则k的值为 .
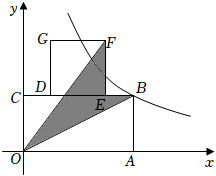 12. 如图,在中, , 点D为的中点,过点C作交的延长线于点E , 若 , , 则的长为 .
12. 如图,在中, , 点D为的中点,过点C作交的延长线于点E , 若 , , 则的长为 .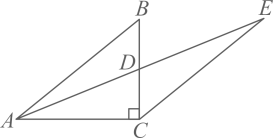 13. 如图,在中, , 点在上,过点作的垂线 , 连接 , 若 , , , , 则的长为 .
13. 如图,在中, , 点在上,过点作的垂线 , 连接 , 若 , , , , 则的长为 .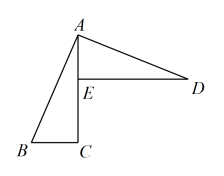 14. 如图,在Rt△ABC中,AC=BC,点P是BC上一点,BD⊥AP交AP延长线于点D,连接CD.若图中两阴影三角形的面积之差为32(即S△ACP-S△PBD=32),则CD=
14. 如图,在Rt△ABC中,AC=BC,点P是BC上一点,BD⊥AP交AP延长线于点D,连接CD.若图中两阴影三角形的面积之差为32(即S△ACP-S△PBD=32),则CD= 15. 如图,点G是正方形ABCD边AB上的一点,连结CG,过点C作 , 交AD的延长线于点E,过点E作 , 过点G作 , EF和GF交于点F,延长CD交EF于点H,连结GH,以HD和DA为边作矩形ADHI.记的面积为 , 的面积为 , 矩形ADHI的面积为 , 若 , , 则 .
15. 如图,点G是正方形ABCD边AB上的一点,连结CG,过点C作 , 交AD的延长线于点E,过点E作 , 过点G作 , EF和GF交于点F,延长CD交EF于点H,连结GH,以HD和DA为边作矩形ADHI.记的面积为 , 的面积为 , 矩形ADHI的面积为 , 若 , , 则 .
三、作图题
-
16. 如图,中,点D在边AC上,且 .
 (1)、请用无刻度的直尺和圆规作出的平分线(保留作图痕迹,不写作法).(2)、若(1)中所作的角平分线与边BC交于点E,连接DE.求证: .17. 如图,在正方形网格中,的三个顶点都在格点上,只用无刻度的直尺作图.
(1)、请用无刻度的直尺和圆规作出的平分线(保留作图痕迹,不写作法).(2)、若(1)中所作的角平分线与边BC交于点E,连接DE.求证: .17. 如图,在正方形网格中,的三个顶点都在格点上,只用无刻度的直尺作图.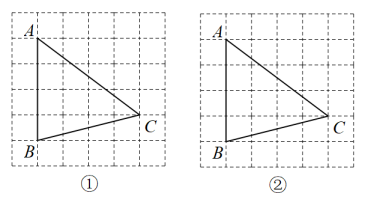 (1)、在图①中,作的角平分线;(2)、在图②中,在边上找一点D,使得.18. 下面是“作一个角的平分线”的尺规作图过程.
(1)、在图①中,作的角平分线;(2)、在图②中,在边上找一点D,使得.18. 下面是“作一个角的平分线”的尺规作图过程.已知:如图,钝角 . 求作:射线 , 使 .
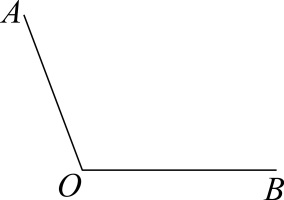
作法:
①在射线上任取一点;
②以点为圆心,长为半径作弧,交于点;
③分别以点为圆心,大于长为半径作弧,在内,两弧相交于点;
④作射线 . 则为所求作的射线.
(1)、使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接CD,CE,
由作图步骤②可知OD= ▲ ,
由作图步费③可知CD= ▲ ,
∵OC=OC,
∴△OCD≅△OCE.
∴∠AOC=∠BOC( )(填推理的依据).
四、解答题
-
19. 如图,在中, , 分别是边和上的点,连接 , , 且 . 求证:
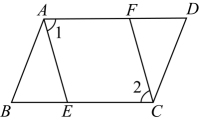 (1)、;(2)、 .20. 如图,已知平分 , 求证:≌ .
(1)、;(2)、 .20. 如图,已知平分 , 求证:≌ .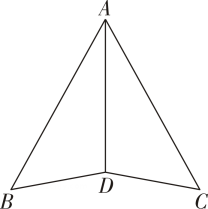 21. 如图,点 , , , 在同一条直线上, , , 求证: .
21. 如图,点 , , , 在同一条直线上, , , 求证: . 22. 如图,在等腰直角三角形和中, , 点在边上,与交于点 , 连接 .
22. 如图,在等腰直角三角形和中, , 点在边上,与交于点 , 连接 .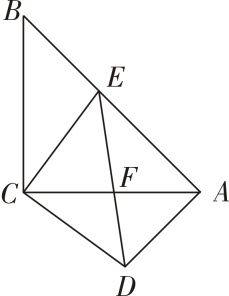 (1)、求证:≌ .
(1)、求证:≌ .
(2)、求证: .五、综合题
-
23. 如图, , , , 垂足分别为 , .
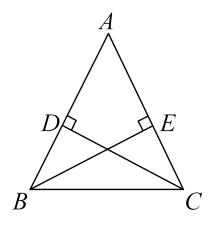 (1)、求证:;(2)、若 , , 求的长.24. 如图,点D、E分别是AB、AC的中点,BE、CD相交于点O,∠B=∠C,BD=CE.求证:
(1)、求证:;(2)、若 , , 求的长.24. 如图,点D、E分别是AB、AC的中点,BE、CD相交于点O,∠B=∠C,BD=CE.求证: (1)、OD=OE;(2)、△ABE≌△ACD.25. 如图.点A,B,C,D在同一条直线上,点E,F分别在直线的两侧,且 , . .
(1)、OD=OE;(2)、△ABE≌△ACD.25. 如图.点A,B,C,D在同一条直线上,点E,F分别在直线的两侧,且 , . .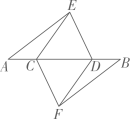 (1)、求证:;(2)、若 , , 求的长.26. 在直线m上依次取互不重合的三个点D,A,E,在直线m上方有AB=AC,且满足∠BDA=∠AEC=∠BAC=α.
(1)、求证:;(2)、若 , , 求的长.26. 在直线m上依次取互不重合的三个点D,A,E,在直线m上方有AB=AC,且满足∠BDA=∠AEC=∠BAC=α. (1)、如图1,当α=90°时,猜想线段DE,BD,CE之间的数量关系是;(2)、如图2,当0°<α<180°时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;(3)、拓展与应用:如图3,当α=120°时,点F为∠BAC平分线上的一点,且AB=AF,分别连接FB,FD,FE,FC,试判断△DEF的形状,并说明理由.
(1)、如图1,当α=90°时,猜想线段DE,BD,CE之间的数量关系是;(2)、如图2,当0°<α<180°时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;(3)、拓展与应用:如图3,当α=120°时,点F为∠BAC平分线上的一点,且AB=AF,分别连接FB,FD,FE,FC,试判断△DEF的形状,并说明理由.