(人教版)2024年中考数学一轮复习 图形的变化--投影与视图 练习题
试卷更新日期:2023-11-28 类型:一轮复习
一、选择题
-
1. 如图所示的几何体的俯视图是( )
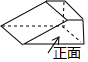 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列四个几何体中,三视图中不含矩形的是( )A、
2. 下列四个几何体中,三视图中不含矩形的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图所示的几何体,其左视图是( )
3. 如图所示的几何体,其左视图是( )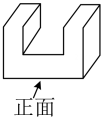 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图是某几何体的三视图,则这个几何体是( )
4. 如图是某几何体的三视图,则这个几何体是( ) A、圆锥
A、圆锥
B、圆柱
C、三棱锥
D、三棱柱5. 把一个正五棱柱如图摆放,光线由上向下照射,此正五棱柱的正投影是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 下列几何体中,主视图是长方形的为( )A、
6. 下列几何体中,主视图是长方形的为( )A、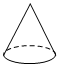 B、
B、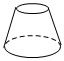 C、
C、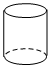 D、
D、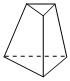 7. 如图所示的立体图形的主视图是( )
7. 如图所示的立体图形的主视图是( )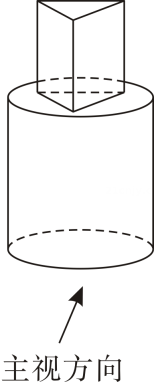 A、
A、
B、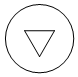
C、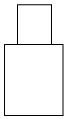
D、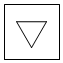 8. 如图所示几何体,从左面看是( )
8. 如图所示几何体,从左面看是( )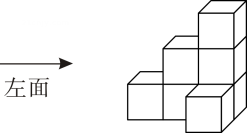 A、
A、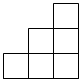 B、
B、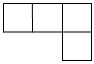 C、
C、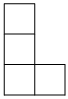 D、
D、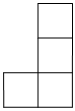 9. 一个正五棱柱如右图摆放,光线由上到下照射此正五棱柱时的正投影是( )
9. 一个正五棱柱如右图摆放,光线由上到下照射此正五棱柱时的正投影是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 某几何体的三视图如图所示,该几何体是( )
10. 某几何体的三视图如图所示,该几何体是( )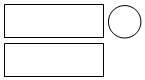 A、三棱柱 B、正方体 C、圆锥 D、圆柱
A、三棱柱 B、正方体 C、圆锥 D、圆柱二、填空题
-
11. 公元前6世纪,古希腊学者泰勒斯用图1的方法巧测金字塔的高度.如图2,小明仿照这个方法,测量圆锥形小山包的高度,已知圆锥底面周长为62.8 m. 先在小山包旁边立起一根木棒,当木棒影子长度等于木棒高度时,测得小山包影子AB长为23 m(直线AB过底面圆心),则小山包的高为m(π取3.14).

 12. 如图所示是某几何体的三视图,根据图中数据计算,这个几何体的侧面积为 .
12. 如图所示是某几何体的三视图,根据图中数据计算,这个几何体的侧面积为 .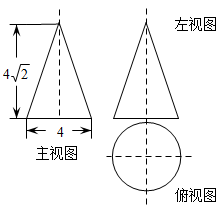 13. 三棱柱的三视图如图所示,在俯视图△EFG中,FG=18cm,EG=14cm,∠EGF=30°,则左视图中AB的长为cm.
13. 三棱柱的三视图如图所示,在俯视图△EFG中,FG=18cm,EG=14cm,∠EGF=30°,则左视图中AB的长为cm. 14. 小明的身高为1.6m,某一时刻他在阳光下的影子长为2m,与他邻近的一棵树的影长为10m,则这棵树的高为m.15. 将7个棱长为1的小立方体摆成如图所示几何体,该几何体的俯视图的面积为.
14. 小明的身高为1.6m,某一时刻他在阳光下的影子长为2m,与他邻近的一棵树的影长为10m,则这棵树的高为m.15. 将7个棱长为1的小立方体摆成如图所示几何体,该几何体的俯视图的面积为.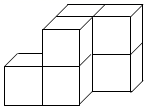
三、解答题
-
16. 某小组的项目式学习活动内容是测量某棵古树的高度 , 如图,在阳光下,某一时刻,古树的影子落在了地上和围墙上,落在地上的长度米,落在墙上的长度米,在古树的附近有一棵小树 , 同一时刻,小树的影长米,小树的高米.已知点N,P,B,D在一条水平线上, , , , 请求出该古树的高度 .
 17. “创新实践”小组想利用所学知识测量大树的高度,因大树底部有障碍物,无法直接测量到大树底部的距离,他们制定了如下的测量方案:如图所示,小丽通过调整测角仪的位置,在大树周围的点C处用测角仪测得大树顶部A的仰角为(测角仪的高度忽略不计).接着,小丽沿着方向向前走3米(即米),到达大树在太阳光下的影子末端D处,此时小明测得小丽在太阳光下的影长为2米.已知小丽的身高为1.5米,B、C、D、F四点在同一直线上, , 求这棵大树的高度.
17. “创新实践”小组想利用所学知识测量大树的高度,因大树底部有障碍物,无法直接测量到大树底部的距离,他们制定了如下的测量方案:如图所示,小丽通过调整测角仪的位置,在大树周围的点C处用测角仪测得大树顶部A的仰角为(测角仪的高度忽略不计).接着,小丽沿着方向向前走3米(即米),到达大树在太阳光下的影子末端D处,此时小明测得小丽在太阳光下的影长为2米.已知小丽的身高为1.5米,B、C、D、F四点在同一直线上, , 求这棵大树的高度.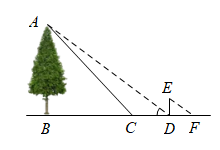 18. 小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.
18. 小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.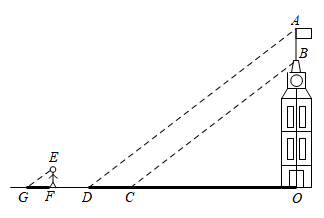 19. 小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆 影子恰好落在水平地面 和斜坡坡面 上,测得旗杆在水平地面上的影长 ,在斜坡坡面上的影长 ,太阳光线 与水平地面成 角,且太阳光线 与斜坡坡面互相垂直,请你帮小明求出旗杆 的高度(结果保留根号).
19. 小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆 影子恰好落在水平地面 和斜坡坡面 上,测得旗杆在水平地面上的影长 ,在斜坡坡面上的影长 ,太阳光线 与水平地面成 角,且太阳光线 与斜坡坡面互相垂直,请你帮小明求出旗杆 的高度(结果保留根号).
四、综合题
-
20. 下图是一个几何体的三视图,其中俯视图为正三角形.
 (1)、这个几何体的名称为 .(2)、求该几何体的左视图中a的值.21. 如图,一根灯杆上有一盏路灯A,路灯A离水平地面的高度为9米,在距离路灯正下方B点15.5米处有一坡度为的斜坡 , 如果高为3米的标尺竖立地面上,垂足为F,它的影子的长度为4米.
(1)、这个几何体的名称为 .(2)、求该几何体的左视图中a的值.21. 如图,一根灯杆上有一盏路灯A,路灯A离水平地面的高度为9米,在距离路灯正下方B点15.5米处有一坡度为的斜坡 , 如果高为3米的标尺竖立地面上,垂足为F,它的影子的长度为4米. (1)、当影子全在水平地面上(图1),求标尺与路灯间的距离;(2)、当影子一部分在水平地面上,一部分在斜坡上(图2),求此时标尺与路灯间的距离为多少米?22. 某校数学社团开展“探索生活中的数学”研学活动,准备测量秦始皇雕塑的高度.如图所示,首先,在阳光下,某一时刻,小玉在雕塑影子顶端处竖立一根高2米的标杆 , 此时测得标杆的影子为2米;然后,在处竖立一根高2.5米的标杆 , 小婷从处沿后退0.8米到处恰好看到点、在一条直线上,小婷的眼睛到地面的距离米,米,已知 , , , , 点、、、、在同一水平直线上,请根据以上数据求出秦始皇雕塑的高度.
(1)、当影子全在水平地面上(图1),求标尺与路灯间的距离;(2)、当影子一部分在水平地面上,一部分在斜坡上(图2),求此时标尺与路灯间的距离为多少米?22. 某校数学社团开展“探索生活中的数学”研学活动,准备测量秦始皇雕塑的高度.如图所示,首先,在阳光下,某一时刻,小玉在雕塑影子顶端处竖立一根高2米的标杆 , 此时测得标杆的影子为2米;然后,在处竖立一根高2.5米的标杆 , 小婷从处沿后退0.8米到处恰好看到点、在一条直线上,小婷的眼睛到地面的距离米,米,已知 , , , , 点、、、、在同一水平直线上,请根据以上数据求出秦始皇雕塑的高度.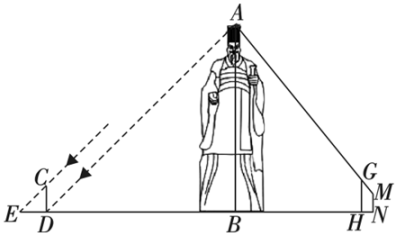 23. 为提高数学学习的兴趣,某学校数学社团利用周日举行了测量旗杆高度的活动.已知旗杆的底座高1米,长8米,宽6米,旗杆位于底座中心.
23. 为提高数学学习的兴趣,某学校数学社团利用周日举行了测量旗杆高度的活动.已知旗杆的底座高1米,长8米,宽6米,旗杆位于底座中心.测量方法如下:在地面上找一点D,用测角仪测出看旗杆AB顶B的仰角为67.4°,沿DE方向走4.8米到达C地,再次测得看旗杆顶B的仰角为73.5°.

 (1)、求旗杆的高度.(2)、已知夏至日时该地的最大太阳高度约为78°,试问夏至日旗杆顶B的影子能不能落在台阶上?(太阳高度角是指某地太阳光线与地平线的夹角.结果精确到0.1m,参考数据:tan67.4°≈2.4,tan73.5°≈ , tan22.6°≈ , tan16.5°≈ , tan12°≈0.21)
(1)、求旗杆的高度.(2)、已知夏至日时该地的最大太阳高度约为78°,试问夏至日旗杆顶B的影子能不能落在台阶上?(太阳高度角是指某地太阳光线与地平线的夹角.结果精确到0.1m,参考数据:tan67.4°≈2.4,tan73.5°≈ , tan22.6°≈ , tan16.5°≈ , tan12°≈0.21)