(人教版)2024年中考数学一轮复习 图形的变化--锐角三角函数 练习题
试卷更新日期:2023-11-28 类型:一轮复习
一、选择题
-
1. 在下列计算中,正确的是( )A、 B、 C、 D、2. 爬坡时坡角与水平面夹角为α,则每爬1m耗能 , 若某人爬了1000m,该坡角为30°,则他耗能( ).(参考数据: , )
 A、58J B、159J C、1025J D、1732J3. 如图,一条河两岸互相平行,为测得此河的宽度PT(PT与河岸PQ垂直),测P、Q两点距离为m米, , 则河宽PT的长度是( )
A、58J B、159J C、1025J D、1732J3. 如图,一条河两岸互相平行,为测得此河的宽度PT(PT与河岸PQ垂直),测P、Q两点距离为m米, , 则河宽PT的长度是( ) A、 B、 C、 D、4. 如图,海中有一小岛 , 在点测得小岛在北偏东方向上,渔船从点出发由西向东航行到达点,在点测得小岛恰好在正北方向上,此时渔船与小岛的距离为 . ( )
A、 B、 C、 D、4. 如图,海中有一小岛 , 在点测得小岛在北偏东方向上,渔船从点出发由西向东航行到达点,在点测得小岛恰好在正北方向上,此时渔船与小岛的距离为 . ( )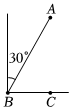 A、 B、 C、 D、5. 在中, , , , 那么的正弦值是( )A、 B、 C、 D、6. 如果把三边的长度都扩大为原来的倍,那么锐角的四个三角比的值( )A、都扩大为原来的倍 B、都缩小为原来的
A、 B、 C、 D、5. 在中, , , , 那么的正弦值是( )A、 B、 C、 D、6. 如果把三边的长度都扩大为原来的倍,那么锐角的四个三角比的值( )A、都扩大为原来的倍 B、都缩小为原来的
C、都没有变化 D、都不能确定7. 以下是某数学兴趣小组开展的课外探究活动,探究目的:测量小河两岸的距离,探究过程:在河两岸选取相对的两点P、A,在小河边取的垂线上的一点C,测得米, , 则小河宽等于( )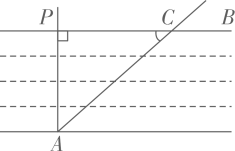 A、米 B、米 C、米 D、米8. 如图,已知是的直径,内接于 , 若 , , 则的值为( )
A、米 B、米 C、米 D、米8. 如图,已知是的直径,内接于 , 若 , , 则的值为( ) A、 B、 C、 D、9. 如图,某飞机于空中A处探测到正下方的地面目标C , 此时飞机高度为1400米,从飞机上看地面控制点B的俯角为 , 则B、C之间的距离为( )
A、 B、 C、 D、9. 如图,某飞机于空中A处探测到正下方的地面目标C , 此时飞机高度为1400米,从飞机上看地面控制点B的俯角为 , 则B、C之间的距离为( )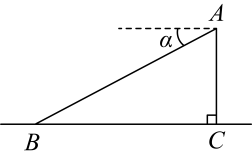 A、米 B、米 C、米 D、米10. 一张小凳子的结构如图所示, , , , 则等于( ).
A、米 B、米 C、米 D、米10. 一张小凳子的结构如图所示, , , , 则等于( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
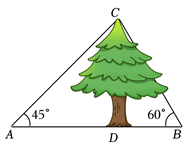
11. 计算: .12. 如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=20m,则这棵树CD的高度约为 m.(按四舍五入法将结果保留小数点后一位,参考数据:)
 13. 已知是锐角,且 , 那么 .14. 如图,在 的正方形网格图中,已知点A、B、C、D、O均在格点上,其中A、B、D又在 上,点E是线段 与 的交点.则 的正切值为.
13. 已知是锐角,且 , 那么 .14. 如图,在 的正方形网格图中,已知点A、B、C、D、O均在格点上,其中A、B、D又在 上,点E是线段 与 的交点.则 的正切值为.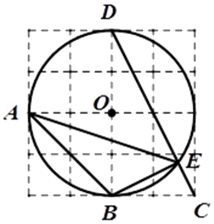 15. 如图所示,在四边形ABCD中,∠B=90°,AB=2,CD=8.连接AC,AC⊥CD,若sin∠ACB= ,则AD长度是.
15. 如图所示,在四边形ABCD中,∠B=90°,AB=2,CD=8.连接AC,AC⊥CD,若sin∠ACB= ,则AD长度是.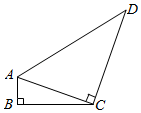
三、解答题
-
16. 计算 .17. 教室里的投影仪投影时,可以把投影光线CA,CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC, . 黑板上投影图像的高度 , CB与AB的夹角 , 求AC的长.(结果精确到1cm.参考数据: , , )
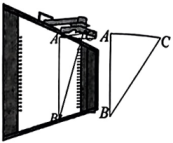 18. 越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A处安置测倾器,测得点M的仰角 ,在与点A相距3.5米的测点D处安置测倾器,测得点M的仰角 (点A,D与N在一条直线上),求电池板离地面的高度 的长.(结果精确到1米;参考数据: )
18. 越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A处安置测倾器,测得点M的仰角 ,在与点A相距3.5米的测点D处安置测倾器,测得点M的仰角 (点A,D与N在一条直线上),求电池板离地面的高度 的长.(结果精确到1米;参考数据: ) 19. 某商店窗前计划安装如图所示的遮阳棚,其截面图如图所示,在截面图中,墙面垂直于地面 , 遮阳棚与墙面连接处点距地面高 , 即 , 遮阳棚与窗户所在墙面垂直,即 , 假设此地正午时太阳光与地面的夹角恰为若经过点的光线恰好照射在地面点处,则 , 为使正午时窗前地面上能有宽的阴影区域,即 , 求遮阳棚的宽度结果精确到 , 参考数据:
19. 某商店窗前计划安装如图所示的遮阳棚,其截面图如图所示,在截面图中,墙面垂直于地面 , 遮阳棚与墙面连接处点距地面高 , 即 , 遮阳棚与窗户所在墙面垂直,即 , 假设此地正午时太阳光与地面的夹角恰为若经过点的光线恰好照射在地面点处,则 , 为使正午时窗前地面上能有宽的阴影区域,即 , 求遮阳棚的宽度结果精确到 , 参考数据:
四、综合题
-
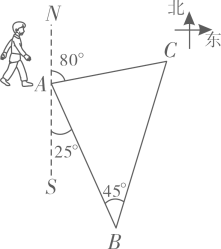
20. 为了增强学生体质、针炼学生意志,某校组织一次定向越野拉练活动.如图,A点为出发点,途中设置两个检查点,分别为点和点,行进路线为.点在点的南偏东方向处,点在点的北偏东方向,行进路线AB和BC所在直线的夹角为.
⑴求行进路线BC和CA所在直线的夹角的度数;
⑵求检查点和之间的距离(结果保留根号).
 21. 如图,为的直径,点C在上,与相切于点A , 与延长线交于点B , 过点B作 , 交的延长线于点D .
21. 如图,为的直径,点C在上,与相切于点A , 与延长线交于点B , 过点B作 , 交的延长线于点D . (1)、求证:;(2)、点F为上一点,连接 , , 与交于点G . 若 , , , 求的半径及的长.
(1)、求证:;(2)、点F为上一点,连接 , , 与交于点G . 若 , , , 求的半径及的长.