(人教版)2024年中考数学一轮复习 图形的变化--图形的相似 练习题
试卷更新日期:2023-11-28 类型:一轮复习
一、选择题
-
1. 如图,在中,是边上的点, , :: , 则与的面积比是( )
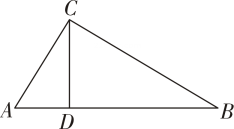 A、:
A、:
B、:
C、:
D、:2. 如图,已知 , 它们依次交直线、于点、、和点、、 , 如果:: , , 那么的长等于( ) A、 B、 C、 D、3. 如图,与是位似图形,点为位似中心,已知:: , 则与的周长比是( )
A、 B、 C、 D、3. 如图,与是位似图形,点为位似中心,已知:: , 则与的周长比是( ) A、: B、: C、: D、:4. 如图,与是位似图形,点是位似中心,若:: , 的面积为 , 则的面积为( )
A、: B、: C、: D、:4. 如图,与是位似图形,点是位似中心,若:: , 的面积为 , 则的面积为( )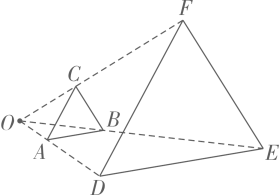 A、 B、 C、 D、5. 两个相似三角形的周长比是.则其相似比是( )A、 B、 C、 D、6. 如图,在正方形网格中,与位似,则下列说法正确的是( )
A、 B、 C、 D、5. 两个相似三角形的周长比是.则其相似比是( )A、 B、 C、 D、6. 如图,在正方形网格中,与位似,则下列说法正确的是( ) A、位似中心是点 B、位似中心是点 C、位似比为 D、位似比为7. 如图,在平行四边形中,点E在边上, , 连接交于点F,则的面积与的面积之比为( )
A、位似中心是点 B、位似中心是点 C、位似比为 D、位似比为7. 如图,在平行四边形中,点E在边上, , 连接交于点F,则的面积与的面积之比为( )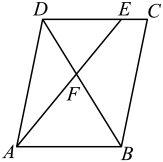 A、 B、 C、 D、8. 如图, , , , 则为( )
A、 B、 C、 D、8. 如图, , , , 则为( ) A、8 B、 C、 D、109. 在平面直角坐标系中,以原点O为位似中心,作的位似图形 , 与相似比为 , 若点A的坐标为 , 则点的坐标为( )A、或 B、或 C、或 D、或10. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上,若线段 , 则线段的长是( )
A、8 B、 C、 D、109. 在平面直角坐标系中,以原点O为位似中心,作的位似图形 , 与相似比为 , 若点A的坐标为 , 则点的坐标为( )A、或 B、或 C、或 D、或10. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上,若线段 , 则线段的长是( ) A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
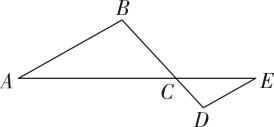
11. 如图, , 若 , , , 则 .
 12. 在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则树的高度为米.13. 如图,在平面直角坐标系中,已知点、 , 以原点O为位似中心,相似比为 , 把缩小,则点B的对应点的坐标是 .
12. 在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则树的高度为米.13. 如图,在平面直角坐标系中,已知点、 , 以原点O为位似中心,相似比为 , 把缩小,则点B的对应点的坐标是 .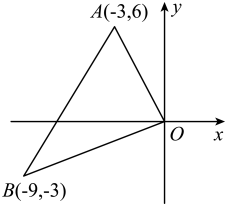 14. 如图, , 若 , , , 则的长为 .
14. 如图, , 若 , , , 则的长为 .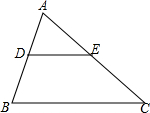 15. 若 , 则 .
15. 若 , 则 .三、解答题
-
16. 《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D点观察井内水岸C点,视线DC与井口的直径AB交于点E.如果测得AB=1.8米,BD=1米,BE=0.2米.请求出井深AC的长.
 17. 如图,在Rt△ABC中, ,D是AB的中点,过D点作AB的垂线交AC于点E,若BC=6,sinA= ,求DE的长.
17. 如图,在Rt△ABC中, ,D是AB的中点,过D点作AB的垂线交AC于点E,若BC=6,sinA= ,求DE的长.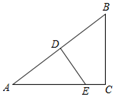
18. 如图,点D在△ABC的边AB上,∠ACD=∠B,AD=6cm,DB=8cm,求:AC的长. 19. 周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
19. 周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.

四、综合题
-
20. 如图,在 中, , 分别是 , 边上的点,且 : : : .
 (1)、求证: ∽ ;(2)、若 ,求 的长.21. 如图, , .
(1)、求证: ∽ ;(2)、若 ,求 的长.21. 如图, , .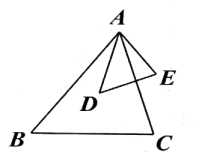 (1)、与相似吗?为什么?(2)、如果 , , 那么的长为多少?22. 如图,在 中, 为 上一点, .
(1)、与相似吗?为什么?(2)、如果 , , 那么的长为多少?22. 如图,在 中, 为 上一点, .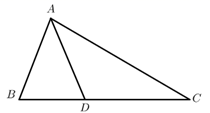 (1)、求证: .(2)、若 ,求 的长.23. 问题提出:已知矩形 , 点为上的一点, , 交于点 . 将绕点顺时针旋转得到 , 则与有怎样的数量关系.
(1)、求证: .(2)、若 ,求 的长.23. 问题提出:已知矩形 , 点为上的一点, , 交于点 . 将绕点顺时针旋转得到 , 则与有怎样的数量关系. (1)、【问题探究】
(1)、【问题探究】探究一:如图,已知正方形 , 点为上的一点, , 交于点 .
如图1,直接写出的值;(2)、将绕点顺时针旋转到如图所示的位置,连接、 , 猜想与的数量关系,并证明你的结论;(3)、探究二:如图,已知矩形 , 点为上的一点, , 交于点 .如图3,若四边形为矩形, , 将绕点顺时针旋转得到、的对应点分别为、点 , 连接、 , 则的值是否随着的变化而变化.若变化,请说明变化情况;若不变,请求出的值.
(4)、【一般规律】
如图3,若四边形为矩形, , 其它条件都不变,将绕点顺时针旋转得到 , 连接 , , 请直接写出与的数量关系.