【北师大版·数学】2024年中考一轮复习之角的平分线和线段的垂直平分线
试卷更新日期:2023-11-28 类型:一轮复习
一、选择题
-
1. 观察下列尺规作图的痕迹:

其中,能够说明的是( )
A、①② B、②③ C、①③ D、③④2. 在中, , , 是上的一点,若的周长比的周长大3,根据下列尺规作图痕迹可以得到符合条件的的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图,是的外接圆,在弧上找一点 , 使点平分弧 . 以下是嘉嘉和琪琪两位同学提供的两种不同的作法:
3. 如图,是的外接圆,在弧上找一点 , 使点平分弧 . 以下是嘉嘉和琪琪两位同学提供的两种不同的作法:嘉嘉:如图1,作的平分线 , 交弧于点 , 则点即为所求.
琪琪:如图2,作的垂直平分线 , 交弧于点 , 则点即为所求.

对于上面的两种作图方法,下面的说法正确的是( )
A、嘉嘉的作法正确 B、琪琪的作法正确 C、嘉嘉和琪琪的作法都错误 D、嘉嘉和琪琪的作法都正确4. 如图,在 中,作以 为内角,四个顶点都在 边上的菱形时,如下的作图步骤是打乱的.①分别以点A、G圆心,大于 长为半径在AG两侧作弧,两弧相交于点M、N;②作直线MN分别交AB、AC于点P、Q,连接PG、GQ;③分别以点D、E为圆心,大于 的长为半径作弧,两弧相交于 内一点F,连接AF并延长交边BC于点G;④以点A为圆心,适当的长为半径作弧,分别交AB、AC于点D、E.则正确的作图步骤是( ) A、②④①③ B、④③②① C、②④③① D、④③①②5. 下列选项中的尺规作图(各图中的点P,都在△ABC的边长),能推出PA=PC的是( )A、
A、②④①③ B、④③②① C、②④③① D、④③①②5. 下列选项中的尺规作图(各图中的点P,都在△ABC的边长),能推出PA=PC的是( )A、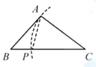 B、
B、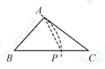 C、
C、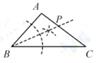 D、
D、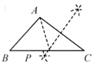 6. 在以下三个图形中,根据尺规作图的痕迹,能判断射线AD平分∠BAC的是( )
6. 在以下三个图形中,根据尺规作图的痕迹,能判断射线AD平分∠BAC的是( )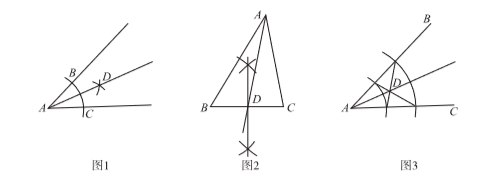 A、图2 B、图1与图2 C、图1与图3 D、图2与图37. 根据圆规作图的痕迹,可用直尺成功地找到 边的中点的是( )A、
A、图2 B、图1与图2 C、图1与图3 D、图2与图37. 根据圆规作图的痕迹,可用直尺成功地找到 边的中点的是( )A、 B、
B、 C、
C、 D、
D、 8. 尺规作图要求:I、过直线外一点作这条直线的垂线:II、作线段的垂直平分线;III、过直线上一点作这条直线的垂线: IV、 作角的平分线.如图是按上述要求排乱顺序的尺规作图:
8. 尺规作图要求:I、过直线外一点作这条直线的垂线:II、作线段的垂直平分线;III、过直线上一点作这条直线的垂线: IV、 作角的平分线.如图是按上述要求排乱顺序的尺规作图:
则正确的配对是( )
A、①-IV,②-II,③-I,④-III B、①-IV, ②-I,③-II,④-I C、①-II,②-IV,③-1II,④-I D、①-IV,②-I,③-II,④-III9. 尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:
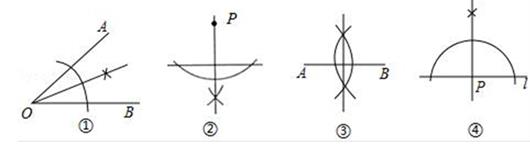
则正确配对是( )
A、①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ B、①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ C、①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ D、①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ10. 小明用尺规作了如下四幅图形:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线,从保留的作图痕迹看出作图正确的是( )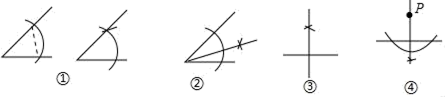 A、①②④ B、②③ C、①③④ D、①②③④
A、①②④ B、②③ C、①③④ D、①②③④二、填空题
-
11. 如图,在 中, 垂直平分AB , 垂足为Q , 交BC于点P . 按以下步骤作图:以点A为圆心,以适当的长为半径作弧,分别交边AC , AB于点D , E;分别以点D , E为圆心,以大于 的长为半径作弧,两弧相交于点F;作射线AF , 射线AF与直线PQ相交于点G , 则 的度数为度.
 12. 如图,△ABC中,∠B=35°,∠BCA=75°,请依据尺规作图的作图痕迹,计算∠α=°
12. 如图,△ABC中,∠B=35°,∠BCA=75°,请依据尺规作图的作图痕迹,计算∠α=°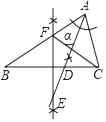 13. 如图,在矩形ABCD中,AB=6,若AD=4,由作图痕迹可得GF= .
13. 如图,在矩形ABCD中,AB=6,若AD=4,由作图痕迹可得GF= . 14. 如图,依据尺规作图的痕迹,计算∠α=°.
14. 如图,依据尺规作图的痕迹,计算∠α=°.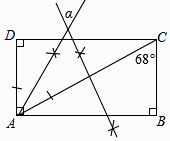
三、作图题
-
15. 尺规作图(保留作图痕迹,不写作法):

如图,已知 , 求作一点P,使平分 , 且
16. 青岛地铁8号线是青岛第六条建成运营的线路,地铁沿线的两个商场A、B与两条道路MF和ME的位置如图所示,其中ME是东西方向的道路,现需要修建一个地铁口(用点O表示),要求点O到两个商场A、B的距离相等,到两条道路MF和ME的距离也相等,且在∠FME的内部.请在示意图中作出一个符合条件的点O.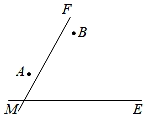 17. 已知:如图,M , N分别是∠BAC两边AB , AC上的点,连接MN . 求作:⊙O , 使⊙O满足以线段MN为弦,且圆心O到∠BAC两边的距离相等.
17. 已知:如图,M , N分别是∠BAC两边AB , AC上的点,连接MN . 求作:⊙O , 使⊙O满足以线段MN为弦,且圆心O到∠BAC两边的距离相等.
四、解答题
-
18. 已知:如图,四边形 .
求作:点 ,使点 在四边形 内部, ,并且点 到 两边的距离相等.
 19.
19.如图,C是∠AOB内部一点,D是∠AOB外部一点,在内部求作一点P,使PC=PD,并且使P点到∠AOB两边距离相等(保留作图痕迹).

五、综合题

