2023-2024学年北师大版数学八年级上册 5.6二元一次方程与一次函数 同步练习(培优卷)
试卷更新日期:2023-11-27 类型:同步测试
一、选择题
-
1. 已知一次函数y=ax—4与y=bx+2图象在x轴上相交于同一点,则的值是( )A、4 B、-2 C、 D、-2. 一次函数与正比例函数为常数,且),它们在同一坐标系中的大致图象是( )A、
 B、
B、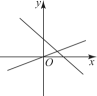 C、
C、 D、
D、 3. 已知直线与的交点的坐标为 , 则a+b的值为( )A、2 B、4 C、8 D、154. 无论m为何实数,直线y=-2x+2m与y=x-4的交点都不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 在平面直角坐标系中,将直线向左平移3个单位后恰好经过原点,则k的值为( )A、-2 B、2 C、-3 D、36. 一次函数 与正比例函数 (m,n为常数、且 )在同一平面直角坐标系中的图可能是( )A、
3. 已知直线与的交点的坐标为 , 则a+b的值为( )A、2 B、4 C、8 D、154. 无论m为何实数,直线y=-2x+2m与y=x-4的交点都不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 在平面直角坐标系中,将直线向左平移3个单位后恰好经过原点,则k的值为( )A、-2 B、2 C、-3 D、36. 一次函数 与正比例函数 (m,n为常数、且 )在同一平面直角坐标系中的图可能是( )A、 B、
B、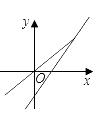 C、
C、 D、
D、 7. 对于函数 , 下列结论正确的是( )A、它的图象经过点 B、它的图象不经过第三象限 C、y值随x的增大而增大 D、它的图象与直线平行8. 已知一次函数的图象经过点 , 且平行于直线 , 则b的值为( )A、 B、1 C、 D、49. 如图,直线l1:y=x+2与直线l2:y=kx+b相交于点P(m,4),则方程组的解是( )
7. 对于函数 , 下列结论正确的是( )A、它的图象经过点 B、它的图象不经过第三象限 C、y值随x的增大而增大 D、它的图象与直线平行8. 已知一次函数的图象经过点 , 且平行于直线 , 则b的值为( )A、 B、1 C、 D、49. 如图,直线l1:y=x+2与直线l2:y=kx+b相交于点P(m,4),则方程组的解是( ) A、 B、 C、 D、10. 在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是( )
A、 B、 C、 D、10. 在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知直线与直线平行,且经过点 , 则的值是 .12. 已知直线y=kx+b与直线y=-3x平行,且经过点(2,4),则b的值是 .13. 已知一直线y=kx+b平行于直线y=-3x+4,且与直线y=2x-6的交点在x轴上,则这条直线的解析式 .14. 如图,一束光线从点O射出,照在经过A(2,0),B(0,2)的镜面上的点D,经AB反射后,反射光线又照到竖立在y轴位置的镜面,经y轴,再反射的光线恰好通过点A,则点D的坐标为.
 15. 如图,直线l1:y=x+1与x轴交于点A,与直线l2:y= x+2交于点B,点C为x轴上的一点,若△ABC为直角三角形,则点C的横坐标为 .
15. 如图,直线l1:y=x+1与x轴交于点A,与直线l2:y= x+2交于点B,点C为x轴上的一点,若△ABC为直角三角形,则点C的横坐标为 .
三、综合题
-
16. 某校为达成省体育器材类装备,计划在京东惠购一次性购进篮球和足球共个,某电商内部信息表给出其进价与售价间的关系如表:
篮球
足球
进价元个
售价元个
(1)、学校用元以进价购进这批篮球和足球,求购进篮球和足球各多少个;
(2)、设该电商所获利润为单位:元 , 购进篮球的个数为单位:个 , 请写出与之间的函数表达式不要求写出的取值范围;
(3)、因资金紧张,学校的进货成本只能在元的限额内,请为学校设计一种进货方案使得尽可能多地购买篮球和足球,同时要使电商利润最小;并求出利润的最小值.17. 已知一次函数 .(1)、当为何值时,该函数的图象经过;(2)、当为何值时,该函数的图象平行于直线 .18. 已知一次函数y=kx+b过点(-2,5),和直线y=-x+3,分别在下列条件下求这个一次函数的解析式.(1)、它的图象与直线y=-x+3平行;(2)、它的图象与y轴的交点和直线y=-x+3直线与y轴的交点关于x轴对称.19. 如图,一次函数y=x+2的图象分别与x轴和y轴交于C,A两点,且与正比例函数y=kx的图象交于点B(﹣1,m). (1)、求正比例函数的表达式;(2)、点D是一次函数图象上的一点,且△OCD的面积是3,求点D的坐标;(3)、在x轴上是否存在点P,使得BP+AP的值最小,若存在,求出点P的坐标,若不存在,说明理由.20. 如图,平面直角坐标系中,直线yx+2与经过A(4,0),B(0,4)两点的直线交于P , 且与x轴,y轴分别交于点C和点D.
(1)、求正比例函数的表达式;(2)、点D是一次函数图象上的一点,且△OCD的面积是3,求点D的坐标;(3)、在x轴上是否存在点P,使得BP+AP的值最小,若存在,求出点P的坐标,若不存在,说明理由.20. 如图,平面直角坐标系中,直线yx+2与经过A(4,0),B(0,4)两点的直线交于P , 且与x轴,y轴分别交于点C和点D. (1)、求直线AB表达式及点P的坐标;(2)、设点E在y轴负半轴上,且与点A , B构成等腰三角形,请求写出点E的坐标.
(1)、求直线AB表达式及点P的坐标;(2)、设点E在y轴负半轴上,且与点A , B构成等腰三角形,请求写出点E的坐标.